
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методика статистической обработки результатов измеренияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Одной из важнейших задач является оценка точности определенного технологического процесса изготовления детали. Такая оценка включает анализ точности изготовления деталей, установление влияния износа оборудования на точность размеров, проверку правильности настройки оборудования и т.д. В настоящее время оценка точности технологического процесса осуществляется с использованием математической статистики и теории вероятности. Как при изготовлении, так и при измерении возникают две категории погрешностей: систематические и случайные. Систематическими называются погрешности, постоянные по величине и знаку или изменяющиеся по определенному закону в зависимости от характера неслучайных факторов. Постоянные систематические погрешности могут являться следствием, например, неточной настройки оборудования, погрешности измерительного прибора и приспособления, отклонения рабочей температуры от нормальной и т.д. Такая погрешность при сохранении условий опыта имеет одну и ту же величину для каждой изготовленной или измеренной детали в партии. Примером переменной систематической погрешности является возрастающая погрешность обработки, называемая износом режущего инструмента. Во многих случаях причины систематических погрешностей могут быть обнаружены и устранены. Систематические погрешности изготовления, которые трудно устранить, должны учитываться допуском на размер и форму детали. Случайными называются непостоянные по величине и знаку погрешности, которые возникают при изготовлении или измерении и принимают то или другое числовое значение в зависимости от случайно действующих причин. Характерным их признаком является вариация значений, принимаемых ими в повторных опытах. Эти погрешности вызываются множеством случайно изменяющихся факторов, таких как припуск на обработку, механические свойства материала, сила резания, измерительная сила и т.д., причем ни один из этих факторов не является доминирующим. Случайные погрешности изготовления проявляются в рассеянии размеров деталей (однотипные детали имеют в одном и том же сечении различные размеры). Наличие случайных погрешностей измерений обнаруживается в том, что при повторном измерении с одинаковой тщательностью одной и той же величины получаются разные числовые результаты. Полностью устранить случайные погрешности невозможно. Но их можно уменьшить, например, в результате более равномерного припуска на обработку, более равномерной твердости и структуры материала заготовок и т.д. Влияние случайных погрешностей учитывается допуском на размер или другой параметр. Значение каждой из случайных погрешностей невозможно заранее определить. С помощью методов теории вероятностей и математической статистики можно приблизительно оценить только пределы изменения и значение суммарной случайной погрешности. Кроме рассмотренных погрешностей, приходится встречаться c грубыми ошибками, обусловленными действием факторов, в нормальных условиях не участвующих в процессе. Например, ошибка при измерении, неправильная настройка сменных колес и т.д. Эти ошибки обычно не учитываются. Выявление погрешностей основывается на применении метода математической статистики и основных положений теории вероятности. Таким методом является метод кривых нормального распределения. Построение и исследование кривых распределения позволяет в ряде случаев предсказать значения полей рассеивания погрешностей, основываясь на обследовании ранее обработанных деталей. Выводы математической статистики основаны на законе больших чисел, согласно которому при увеличении числа наблюдений над однородными явлениями частность появления какого-либо события в прошлом приближается к вероятности появления его в будущем. Порядок построения кривой распределения и обработки результатов измерения рассмотрим на примере. Фактические размеры диаметра с восходящим рядом чисел партии деталей n = 50 шт. показаны в таблице 6.
Таблица 6 – Действительные размеры деталей Размеры в мм
Весь диапазон Xmax... Xmin результатов наблюдений разделить на r интервалов шириной Число интервалов выбирается в зависимости от числа наблюдений согласно рекомендациям таблицы 7. Таблица 7 – Зависимость числа интервалов от числа наблюдений
Принимаем интервал рассеивания равным 0,02 мм и разбиваем все размеры на группы, как показано в таблице 8. Таблица 8 – Распределение действительных размеров по интервалам
Абсолютная частота определяется числом деталей, находящихся в данном интервале размеров. Например, в интервале 7,930 - 7,950 находятся размеры: 7,935; 7.940, т.e. 2 детали и т.д. Вероятность (частость) есть отношение количества деталей данного интервала (n) к общему количеству (N) деталей исследуемой партии 50шт. Например, в интервале размеров 8,010 - 8,030 имеется 10 деталей, вероятность которых составляет
Сумма вероятностей составляет целую единицу, т.е. 100% всех деталей партии. Откладывая в масштабе по оси абсцисс размеры деталей или интервалы, а по оси ординат – вероятность (частость) для каждого интервала размеров и соединяя полученные точки плавной линией, получим кривую распределения. Построить гистограмму наблюдений в виде графика в координатах – длины интервалов удобнее выбирать одинаковыми. Однако если распределение крайне неравномерно, то в области максимальной концентрации результатов наблюдений следует выбирать более узкие интервалы. – масштабы по осям гистограммы должны быть такими, чтобы
Рисунок 13 – Гистограмма распределения результатов измерений Как видно из рисунка 1, кривая нормального распределения имеет выпуклую форму с округленной вершиной, она симметрична, имеет точки перегиба с каждой стороны, за которыми кривая обращена выпуклостью книзу и приближается к оси абсцисс. Кривая нормального распределения определяется функцией
где х – случайная величина; mх – математическое ожидание случайной величины, т.е. значение абсциссы, соответствующее вершине кривой Ymax. Mода кривой mх – есть центр группирования (распределения) и вместе с тем является средней арифметической распределения / Хср /. s – среднеквадратичное отклонение. Точность обработки партии деталей будет характеризоваться средним вероятным размером /Хср /, средним квадратическим отклонением. Среднее арифметическое значение действительных размеров определяется уравнением.
где xi – результат i – го наблюдения n – число наблюдений. Величину xср иногда называют средневзвешенной. Она определяет эмпирический центр группирования. Рассеивание значений случайных величин в выборке относительно эмпирического центра группирования характеризуется эмпирическим средним квадратичным отклонением. Среднее квадратичное отклонение погрешности (СКО):
где Среднее квадратичеcкое отклонение позволяет определить наибольшее рассеивание размеров, которое практически следует учитывать (границы поля рассеивания). В качестве такого предела приняли ± 3s = 6 s. Вероятность получения размера в пределах ±3s составляет 99,73%; следовательно, риск получения размеров, выходящих за эти пределы, будет менее 0,3%. Перечисленные выше погрешности влияют на форму и расположение кривой распределения размеров. Так, например, постоянная погрешность в пределах партии деталей не влияет на форму кривой, но смещает кривую по оси абсцисс (рисунок 14). Погрешность, закономерно изменяющая свое значение в партии заготовок, окажет влияние на форму кривой, вследствие увеличения размаха распределения размеров, определяющего по оси абсцисс (рисунок 15) крайними значениями (рисунок 16). Кривые распределения размеров заготовок, обработанных при различных настройках станка или обмеренных не в одном сечении (в особенности для нежестких деталей), получаются многовершинными.
Рисунок 14 – Кривая нормального распределения
Рисунок 15 – Влияние постоянной погрешности
Рисунок 16 – Влияние закономерно изменяющейся погрешности
Контрольные вопросы и задания 1) Назовите микрометрические инструменты, применяемые для определения размеров деталей, изделий. 2) Назовите основные узлы микрометра. 3) Установите гладкий микрометр на нуль. 4) На шкале микрометра последовательно установите несколько размеров: 5,41; 5,92; 10,12; 15,32 мм. 5) Перечислите метрологические показатели микрометра. 6) Приведите пример обозначения гладкого микрометра 1-го класса точности с пределами измерения от 0 до 25 мм. 7) Объясните обозначение микрометра МК-175-2 ГОСТ 6507-90. 8) Укажите область применения инструмента НМ-175 ГОСТ 10-88. 9) В чем различие между гладким и резьбовым микрометрами? 10) Укажите последовательность установки резьбового микрометра на нуль.
ЛАБОРАТОРНАЯ РАБОТА 3
|
||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 1395; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.111.30 (0.007 с.) |

 и определить частоты ni, равные числу результатов, лежащих в каждом i -м интервале, т. е. меньше или равных его правой и больше левой границы.
и определить частоты ni, равные числу результатов, лежащих в каждом i -м интервале, т. е. меньше или равных его правой и больше левой границы.

 . (9)
. (9)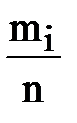 - интервалы значений
- интервалы значений  (рисунок 13). При построении гистограмм рекомендуется пользоваться следующими правилами:
(рисунок 13). При построении гистограмм рекомендуется пользоваться следующими правилами:
 , (10)
, (10) (11)
(11) , (12)
, (12) .– отклонение результата отдельного наблюдения от среднего арифметического равно:
.– отклонение результата отдельного наблюдения от среднего арифметического равно:  . (13)
. (13)



