
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Порядок измерения штангенинструментамиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для отсчета измеряемой величины с помощью нониуса сначала определяют целое число миллиметров перед нулевым делением нониуса по основной шкале (рисунок 7). Затем добавляют к нему число долей по нониусу в соответствии с тем, какой штрих шкалы нониуса ближе к штриху основной шкалы. На рисунке 7 искомый размер равен 13 мм по основной шкале плюс 0,9 мм по подвижной. Один интервал шкалы нониуса, согласно рисунку 6, составляет 0,1 мм. При выполнении внутренних и наружных измерений нужно использовать соответствующие губки или поверхности губок инструментов. Работая со штангенциркулем ШЦ-II и штангенрейсмасом, необходимо помнить о поправках в результатах измерений, которые зависят от толщины губок и измерительной ножки. При измерении детали губки штангенинструментов должны соприкасаться своими поверхностями с измеряемыми поверхностями без перекосов.
Рисунок 7 – Отсчетное устройство штангенинструментов Погрешность измерения и выбор измерительных средств Погрешность измерения равна совокупности погрешностей средства измерения (инструментальная погрешность), метода измерения и др. На примере штангенциркуля рассмотрим инструментальную (основную) погрешность. Её причины - неточность делений штанги и нониуса, отклонение от плоскости и нарушение параллельности измерительных поверхностей, а также перпендикулярности измерительных поверхностей и направляющей грани штанги. Эта погрешность отдельно не нормируется, а входит в суммарную погрешность инструмента. ГОСТ 8.051-81 «ГСИ. Погрешности, допускаемые при измерении линейных размеров до 500 мм» регламентирует допускаемые погрешности измерений линейных параметров до 500 мм (для всех интервалов размеров и квалитетов). В зависимости от размера и точности изготовления детали стандартом устанавливается наибольшая допустимая погрешность измерения, которая включает погрешности средства измерения, установочных мер, температурных деформаций, базирования, а также случайные, неучтенные систематические погрешности измерения. Выбор измерительных средств в общем случае зависит от пределов измерений, допускаемых погрешностей, конструктивных особенностей деталей, масштаба производства и др. Нормальные условия, устанавливаемые ГОСТ 8.050-73 «ГСИ. Нормаль-ные условия выполнения линейных и угловых измерений» (температура окружающей среды +20°С, атмосферное давление 101324,72 Па, относительная влажность воздуха 58% и т. д.), исключают дополнительные погрешности.
Ход работы Оборудование и приборы: штангенциркули ШЦ-I, ШЦ-II ГОСТ 166-89; штангенглубиномеры ГОСТ 162-90; штангенрейсмасы ГОСТ 164-90; штанген-зубомеры; детали; рабочие чертежи деталей. 1) Изучить устройство штангенинструментов, см. рисунок 1 ‒ 6. Ознакомиться с измеряемыми деталями. Для каждой детали вычертить эскиз. 2) Выбрать штангенинструменты для измерения соответствующих параметров и внести их основные значения в таблицу (пример – таблица 1). 3) Измерить линейные размеры штангенинструментом с нониусным и электронным отсчетом, записать полученные данные в протокол измерений
Таблица 1 – Средства измерения
4) Измерить диаметр x деталей, т.е. провести прямые равноточные измерения, в итоге которых значение физической величины находят непосредственно из опытных данных, сравнив измеряемую величину с её мерой или использовав измерительные средства, непосредственно дающие её значения. Равноточными (равнорассеянными) называются прямые независимые измерения постоянной величины, результаты которых могут рассматриваться как случайные, распределенные по одному и тому же закону. В большинстве случаев при обработке прямых равноточных измерений исходят из предположения нормального закона распределения результатов и погреш-ностей измерений. Статистические оценки находят, исходя из конкретного закона распре-деления случайной величины. Обычно предполагается, что диаметр (длина, ширина и т.п.), как случайная измеряемая величина, подчиняется закону нормального распределения. 5) Обработать результаты прямых измерений диаметра (длины), используя точечные оценки соответствующих им характеристик генеральной совокупности. Определить среднеарифметическое значение величины х, т.е.
Если известна систематическая погрешность и она постоянна, то ее исключают из найденной величины математического ожидания. 6) Вычислить среднеквадратичное отклонение (СКО)
или
7) Исключить грубые погрешности (промахи). При однократных измерениях обнаружить грубую погрешность удается не всегда. При многократных измерениях для её обнаружения используют статистические критерии. При этом задаются вероятностью При числе наблюдений n > 20 используют, как правило, критерий трех сигм (критерий Райта). По этому критерию, промахом считается результат наблюдения хi, который отличается от среднего При малом числе наблюдений (n < 20) применяют критерий Романовского (критерий b):
Сначала вычисляют это отношение и сравнивают его с критерием bТ, зависящим от заданного уровня значимости qи числа n наблюдений (таблица 2). При b ³ bТ результат считается промахом и не учитывается 8) Определить границы доверительного интервала, в котором с заданной вероятностью (обеспеченностью) находится случайная погрешность среднеарифметического значения измеряемой величины. Формула расчета –
При числе наблюдений n > 20 значения коэффициента t определяют по таблицам функции Лапласа, см. табл. 3, а при n < 20 – по таблицам функции Стьюдента, см. таблица 3.
Таблица 2 – Значения критерия Романовского bТ при числе измерений n от 4 до 20
Смысл понятий «доверительный интервал» и «доверительная вероятность» состоит в следующем: пусть доверительная вероятность P =0,95, тогда с надежностью 95% можно утверждать, что истинное значение величины xист. не отличается от оцениваемого больше чем на ± D xсл. Таблица 3 – Значения функции Лапласа
Значения коэф-фициентов tp . n в зависимости от P и n представлены в таблице 4. Для того чтобы окончательно установить границы доверительного интервала необходимо расширить его с учетом систематической погрешности ±xсист., которая, как правило, указана в паспорте или на шкале прибора, а в простейших случаях может быть принята равной половине цены деления младшего разряда шкалы. Таблица 4 – Значения коэффициента Стьюдента
9) Оценить относительную погрешность измеряемой физической величины по формуле
10) Найти результат измерения по формуле
На шкалах многих измерительных приборов указывается класс точности. Его условным обозначением является цифра, обведенная «кружком». Класс точности определяет абсолютную приборную погрешность в процентах от наибольшего значения величины, которое может быть измерено данным прибором. Если класс точности на шкале прибора не указан, то абсолютную погрешность принимают равной половине цены наименьшего деления шкалы прибора. При определении абсолютной погрешности прибора по цене деления нужно обращать внимание на метод измерения, а также на то, чем и как регистрируются результаты, каково расстояние между соседними штрихами на шкале прибора. При отсутствии каких-либо указателей (визиров и т.п.) приборная погрешность может быть принята равной цене деления, если указателем прибора является не плавно перемещающаяся, а «скачущая» стрелка (как, например, у ручного секундомера). 11) Оформить отчет. Содержание отчета: 1) название pаботы; 2) цели; 3) общие сведения о штангенинструментах; 4) эскизы деталей с указанием размеров; 5) результаты прямых измерений, определение среднеарифметического значение; границы доверительного интервала; значение относительной погрешности; 6) основные выводы. Контрольные вопросы и задания 1) Объясните устройство штангенциркуля ШЦ-I. 2) Назовите штангенинструменты, применяемые в ходе технических измерений. 3) Назовите нормальные условия окружающей среды, необходимые для линейных измерений (по ГОСТ 8.050-73 «ГСИ. Нормальные условия выполнения линейных и угловых измерений»). 4) Какие измерительные средства применяются для определения размеров внутренних поверхностей деталей? 5) Объясните назначение штангензубомера и назовите его конструктивные особенности. 6) Как выбирается штангенинструмент? Что называется погрешностью измерения? 7) Объясните следующие обозначения: ШЦ-II-200-0,05 ГОСТ 166-89; ШР-250-0,05 ГОСТ 164-90; ШГ-200 ГОСТ 162-90. 8) Каково назначение шкалы нониуса штангенинструмента? 9) Назовите составляющие инструментальной погрешности штангенциркуля
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 2184; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.252.8 (0.009 с.) |


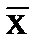 (математическое ожидание
(математическое ожидание 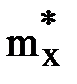 ):
):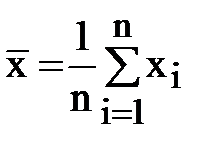 . (1)
. (1)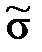 среднеарифметического значения результатов измерений, характеризующего рассеивание,по формуле
среднеарифметического значения результатов измерений, характеризующего рассеивание,по формуле при n > 20 (2)
при n > 20 (2)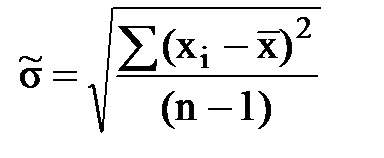 при n < 20. (3)
при n < 20. (3) (уровнем значимости) того, что сомнительный результат, действительно, возможен в данной их совокупности.
(уровнем значимости) того, что сомнительный результат, действительно, возможен в данной их совокупности.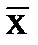 более чем на
более чем на  , т.е.
, т.е.  . Вероятность такого результата
. Вероятность такого результата  .
.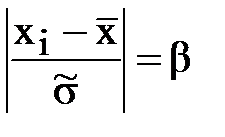 . (4)
. (4) . (5)
. (5)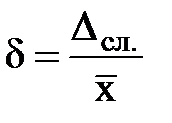 . (6)
. (6)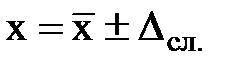 . (7)
. (7)


