
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Попадание в промежуток.Правило 3х сигм.Содержание книги
Поиск на нашем сайте
Равномерное распределение Непрерывная случайная величина имеет равномерное распределение на отрезке [a,b], если на этом отрезке плотность распределения случайной величины постоянна, а вне его равна нулю, т.е.
где С = Const. Используя условие нормировки 2 из § 9, определим С.
откуда с = 1/(b-a) и, следовательно, плотность равномерного распределения имеет вид: Теперь определим вид интегральной функции распределения для этого закона, который в силу (9.1) будет следующим:
Изобразим графики f(x) и F(x):
Определим числовые характеристики данной случайной величины:
Показательное распределение В практических приложениях теории вероятностей, особенно в теории массового обслуживания, исследовании операций, в физике, биологии, теории надежности, часто имеют дело со случайными величинами, которые имеют показательное распределение. Случайная величина распределена по показательному закону с параметром >0, если она непрерывна и имеет следующую плотность распределения вероятностей: Тогда
Определим числовые характеристики: σ=М(x)=1/λ D(x)=1/λ^2
Нормальное распределение Непрерывная случайная величина имеет нормальное распределение вероятностей с параметрами а, s > 0, если плотность распределения ее имеет вид: Нормальный закон распределения широко применяется в практических задачах, он проявляется во всех случаях, когда случайная величина является результатом действия большого числа различных факторов. Каждый фактор в отдельности на величину x влияет незначительно. M(x) = a. D(x) = s 2 Таким образом, параметры а, s 2 в выражении есть математическое ожидание и дисперсия нормально распределенной случайной величины, а
Отметим некоторые свойства нормальной кривой. 1. Кривая распределения симметрична относительно прямой х = а. 2. 3. 4. При изменении математического ожидания и при s = Const, происходит смещение кривой вдоль оси Ох. Если положить а = Const и изменять s, то кривая изменяет свой вид в зависимости от s.
1.Фунция определена и непрерывна на всей числовой оси.2.Функция только положительная. Вероятность попадания НВВ х в промежуток [x1;x2] находится по формуле Р(x1<=X<=x2)=Ф(x2-a/σ)-Ф(x1-a/σ) F(x)=0.5+Ф((x-a)/ s)
Попадание в промежуток.Правило 3х сигм. 1. Вероятность попадания НВВ х в промежуток [x1;x2] находится по формуле Р(x1<=X<=x2)=Ф(x2-a/σ)-Ф(x1-a/σ) Док-во P(x1<X<x2)=Ф(t2)-Ф(t1),где t2=x2-a/σ, t1=x1-a/σ 2. Вероятность того, что модуль отклонения нормально распред. случайной величины х от своего мат.ожидания не превысит величину ε>0,равняется Центральная граничная теорема. Интегр. теорема Муавра-Лапласса и её отдельные случаи ЦГТ: Если все СВ одинаково распределены, то закон распределения их суммы при n стримящ. к бесконечност неограниченно приближается к нормальному. М-Л..Для биноминально распред. ДСВ Х=m-частоты появления события А с вер. Р в серии из n НПВ справедлива формула P(m1<=m<=m2)=Ф(t2)-Ф(t1) Ф(t)-интегр.ф-ция Лапласа t1=m1-np/кор.(npq) Частные случаи Ждя частоты m и частости m/n появления события А с вероятностью р в серии из n НПВ справедливы формулы P(|m-np|<ε)=2Ф(ε/кор(npq)) P(|m/n-p|<ε)=2Ф(ε* кор.(n/pq) Неравенство Маркова Если СВ принимает только неотрицательные значения и имеет фиксированное мат.ожидание,то для любого положительного числа α справедливо неравенство P(X>=α)<=M(X)/α или Р(Х< α)>1-M(X)/ α Доказательство: М(Х)=∫0∞хf(x)dx>=∫α∞xf(x)dx>= α ∫ α∞f(x)dx= αp(x>=α) С. п. г. проводится с помощью статистического критерия по общей логической схеме, включающей нахождение конкретного вида функции от результатов наблюдения (критической статистики), на основании которой принимается окончательное решение.Результат проверки может быть либо отрицательным (данные наблюдения противоречат высказанной гипотезе), либо неотрицательным. В первом случае гипотеза ошибочна, во втором ее нельзя считать доказанной: просто она не противоречит имеющимся выборочным данным, однако таким же свойством могут наряду с ней обладать и другие гипотезы. Теорема суммы Полная вероятность Формула Байеса Формула Бернулли Наивероятнейшаячастота Формула Пуассона Мат ожидание, дисперсия, и Среднее квадратич. Отклонение частоты И частости Мат ожидание Дисперсия Метод моментов Интергральная ф-ция Дифференциальная ф-ци Равномерное распределение Показательное распределение Нормальное распределение Попадание в промежуток Правило 3х сигм И её отдельные случаи Неравенство Маркова Дополнение Ляпунова Точковые оценки выборки Интервальные оценки выборки Статис. проверка гипотез Классическое определение Вероятности. Свойства
Равномерное распределение Непрерывная случайная величина имеет равномерное распределение на отрезке [a,b], если на этом отрезке плотность распределения случайной величины постоянна, а вне его равна нулю, т.е.
где С = Const. Используя условие нормировки 2 из § 9, определим С.
откуда с = 1/(b-a) и, следовательно, плотность равномерного распределения имеет вид: Теперь определим вид интегральной функции распределения для этого закона, который в силу (9.1) будет следующим:
Изобразим графики f(x) и F(x):
Определим числовые характеристики данной случайной величины:
Показательное распределение В практических приложениях теории вероятностей, особенно в теории массового обслуживания, исследовании операций, в физике, биологии, теории надежности, часто имеют дело со случайными величинами, которые имеют показательное распределение. Случайная величина распределена по показательному закону с параметром >0, если она непрерывна и имеет следующую плотность распределения вероятностей: Тогда
Определим числовые характеристики: σ=М(x)=1/λ D(x)=1/λ^2
Нормальное распределение Непрерывная случайная величина имеет нормальное распределение вероятностей с параметрами а, s > 0, если плотность распределения ее имеет вид: Нормальный закон распределения широко применяется в практических задачах, он проявляется во всех случаях, когда случайная величина является результатом действия большого числа различных факторов. Каждый фактор в отдельности на величину x влияет незначительно. M(x) = a. D(x) = s 2 Таким образом, параметры а, s 2 в выражении есть математическое ожидание и дисперсия нормально распределенной случайной величины, а
Отметим некоторые свойства нормальной кривой. 1. Кривая распределения симметрична относительно прямой х = а. 2. 3. 4. При изменении математического ожидания и при s = Const, происходит смещение кривой вдоль оси Ох. Если положить а = Const и изменять s, то кривая изменяет свой вид в зависимости от s.
1.Фунция определена и непрерывна на всей числовой оси.2.Функция только положительная. Вероятность попадания НВВ х в промежуток [x1;x2] находится по формуле Р(x1<=X<=x2)=Ф(x2-a/σ)-Ф(x1-a/σ) F(x)=0.5+Ф((x-a)/ s)
Попадание в промежуток.Правило 3х сигм. 1. Вероятность попадания НВВ х в промежуток [x1;x2] находится по формуле Р(x1<=X<=x2)=Ф(x2-a/σ)-Ф(x1-a/σ) Док-во P(x1<X<x2)=Ф(t2)-Ф(t1),где t2=x2-a/σ, t1=x1-a/σ 2. Вероятность того, что модуль отклонения нормально распред. случайной величины х от своего мат.ожидания не превысит величину ε>0,равняется
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 292; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.42.61 (0.006 с.) |

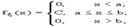
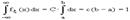 ,
,
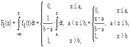 (14.2)
(14.2)

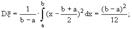
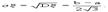 Непрерывная случайная величина подчинена равномерному закону распределения, если ее возможные значения лежат в пределах некоторого определенного интервала, кроме того, в пределах этого интервала все значения случайной величины одинаково вероятны (обладают одной и той же плотностью вероятности).
Непрерывная случайная величина подчинена равномерному закону распределения, если ее возможные значения лежат в пределах некоторого определенного интервала, кроме того, в пределах этого интервала все значения случайной величины одинаково вероятны (обладают одной и той же плотностью вероятности).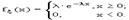
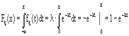 (x > 0). соответственно, графики f(x) и F(x) имеют вид:
(x > 0). соответственно, графики f(x) и F(x) имеют вид: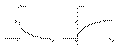
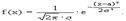
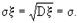 График плотности вероятности имеет вид нормальной кривой (Гаусса):
График плотности вероятности имеет вид нормальной кривой (Гаусса):

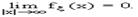

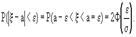 3. Правило 3х сигм.С практической достоверностью (0,9973) можно утверждать, что значения нормально распред.случайной величины Х попадают в промежуток [a-3σ; a+3σ]P(|x-a|<ε)=2Ф(ε/σ)ε=3 σ=2Ф(3σ/σ)=2Ф(3)=1
3. Правило 3х сигм.С практической достоверностью (0,9973) можно утверждать, что значения нормально распред.случайной величины Х попадают в промежуток [a-3σ; a+3σ]P(|x-a|<ε)=2Ф(ε/σ)ε=3 σ=2Ф(3σ/σ)=2Ф(3)=1


