
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Системы цифровых элементов. Состав.Содержание книги
Поиск на нашем сайте
Системы цифровых элементов. Состав. Система цифровых элементов – это совокупность логических, запоминающих и вспомогательных элементов, согласующихся между собой и имеющих единое конструктивное выполнение. Системы цифровых элементов (СЦЭ) классифицируются по двум признакам: типам связи между элементами в схеме; типам приборов, которые используются для реализации тех или иных функций в составе элементов. В зависимости от вида связи различают следующие системы цифровых элементов: потенциальные СЦЭ - отличаются тем, что при построении схемы разрешены только потенциальные связи (рис. 4.1);
Рис. 4.1. Схема связей потенциальных ЛЭ импульсные СЦЭ – при построении схем разрешены только импульсные связи (рис. 4.2);
Рис. 4.2. Схема связей импульсных ЛЭ импульсно- потенциальные СЦЭ, в которых разрешены и те, и другие связи (рис.4.3).
Рис. 4.3. Схема связей импульсно- потенциальных ЛЭ Согласование цифровых элементов означает использование одних и тех же источников питания и одинаковых уровней логических сигналов. Вспомогательными элементами являются различные типы усилителей, формирователей сигналов, схемы согласования и индикаторы. Эти схемы рассматриваются в курсе «Электроника». В настоящее время используют в основном только потенциальные системы элементов. Потенциальные элементы обеспечивают более высокую надежность при передаче информации, а также являются предпочтительными при использовании интегральных технологий, так как в их схемах отсутствуют емкости и индуктивности.
Универсальный JK-триггер Эта схема называется универсальной потому, что на ее основе можно построить все основные типы триггеров. JK-триггер имеет только двухтактную структуру (рис.8.15). УГО JK –триггера изображено на рис.8.16.
Рис. 8.15. Логическая схема JK –триггера
Рис. 8.16. УГО JK –триггера
Рис. 8.17. Временная диаграмма работы JK –триггера На рис. 8.15 представлена логическая схема JK –триггера, которая представляет собой двухступенчатую структуру с обратными связями. Так как схема собрана на ЛЭ “И-НЕ”, то в таблице переходов (табл. 8.4) работа триггера рассматривается в условиях положительной логики. Вход J является входом установки в состояние “1”, вход K – входом установки в “0”. Триггер первой ступени срабатывает по положительному фронту синхроимпульса, а триггер второй ступени управляется инвертированным синхроимпульсом, т.е. срабатывает по отрицательному фронту синхроимпульса через 0.5 такта. Рассмотрим работу триггера, используя временную диаграмму (рис.8.17). В первом такте синхроимпульс С:=0, оба триггера находятся в нулевом состоянии. Во втором такте C:=1,K:=0, J: =1 и положительным фронтом синхроимпульса уста-
навливается триггер Q':=1, а затем через 0,5 такта по заднему фронту это состояние передается во второй триггер Q: =1. Таблица 8.4
В третьем и четвертом тактах С:=1, J:=1, K:=1 и в соответствии с таблицей истинности дважды устанавливаются в противоположное состояние оба триггера. В третьем такте Q':=0 и Q:=0, а в четвертом такте Q':=1 и Q:=1. В пятом такте J:=0, K:=1 и оба триггера устанавливаются в нуль. Наконец, в последнем такте С:=1, J;=1, K:=1 состояние обоих триггеров снова изменяется на противоположное Q':=1, Q: =1.
Счетчики Счетчик – многоразрядный ФУ, предназначенный для подсчета количества импульсов, поступающих на его вход. Схемы счетчиков разнообразны, и их можно классифицировать по нескольким признакам: 1) в зависимости от системы счисления, в которой ведется подсчет числа импульсов, на: а) двоичные; б) двоично-десятичные; 2) по способу организации переноса между разрядами счетчика: а) с последовательным переносом, б) параллельным переносом, в) групповым переносом; 3) в зависимости от арифметической операции, выполняемой счетчиком: а) суммирующие, б) вычитающие, в) реверсивные; 4) по способу управления: а) асинхронные, б) синхронные.
10.3.1 Счетчик с последовательным переносом
Рис.10.6. Двоичный суммирующий счетчик с последовательным переносом асинхронного типа. На рис.10.6 и 10.7 приведены схема и УГО двоичного суммирующего счетчика с последовательным переносом асинхронного типа.
Рис.10.7. УГО счетчика Ниже показана МОДИС- модель этого счетчика и временная диаграмма работы счетчика (рис.10.8). Составим МОДИС- модель этого счетчика. Описание переменных ‘ЗАВИСИМ’ С4 [1:K], Р [1: 2]; ‘ИНЕЗАВ’ Р0, ГШ; Описание схемы С4 [1] ’:=‘ ‘ЕСЛИ’ ГШ ‘ТО’ 0 ‘ИНЕСЛИ’ Р0 ‘ТО’ IC4 [1] ‘ИНАЧЕ’ C4 [1]; Р1 ‘:=‘ C4 [1] * P0 С4 [1:K] ‘:=‘ ‘ЕСЛИ’ ГШ ‘ТО’ 0 ‘ИНЕСЛИ’ Р0 ‘ТО’ C4 [1:K]+1 “ИНАЧЕ’ C4 [1:K];
Рис. 10.8. Временная диаграмма работы счетчика Каждый разряд счетчика делит частоту поступающих на его вход импульсов на 2. У асинхронного счетчика моменты срабатывания
отдельных разрядов счетчика определяются реальными задержками в схемах формирования переноса. τp - время формирования переноса в одном разряде. Быстродействие счетчика определяется временем пробега переноса по всем разрядам. Трег= n * τp – время регистрации – интервал времени от момента поступления на вход счетчика очередного импульса до момента, когда новое значение установится во всех разрядах счетчика. n –количество разрядов в счетчике. 10.3.2. Счетчик с параллельным переносом Как следует из рис. 10.9. счетчик является синхронным, так как срабатывание всех триггеров происходит практически одновременно при поступлении на его вход сигнала Р0. Схемы формирования переносов строятся по следующим формулам: Р1 ‘:=‘ Р0 * Q1; Р2 ‘:=‘ P1 * Q2 = P0 * Q1 * Q2; ...Pк ‘:=’ P0 * Q1 * Q2 *... * Qk-1; Трег≈ τp. Счетчики с параллельным переносом обладают наибольшим быстродействием, причем Трег теоретически не зависит от количества разрядов. Однако на практике такие счетчики строятся не более, чем на 8 разрядов.
Рис. 10.9. Счетчик с параллельным переносом
Реверсивный счетчик Реверсивный счетчик обеспечивает, как суммирование, так и вычитание импульсов из содержимого счетчика. Существуют две основные структуры реверсивных счетчиков: 1) на вход схемы подается одна последовательность входных импульсов, но в каждый момент времени известен ее знак или режим работы счетчика, 2) на вход реверсивного счетчика поступают две последовательности импульсов с разными знаками. Схема, представленная на рис. 10.11, соответствует первой структуре. На вход схемы поступает одна последовательность сигналов. Триггер знака ТЗн определяет режим работы счетчика.
В режиме сложения формируется входной сигнал с положительным знаком и последовательность переносов P0 ’:=‘ ТЗн * X0; в режиме вычитания - последовательность заемов Z0 ‘:=‘ IТЗн * X0; таким образом, на входе первого триггера Q1 появляются две последовательности сигналов с разными знаками, что соответствует второй структуре. На рис.10.12 показано УГО реверсивного счетчика этого типа. Составим МОДИС-описание схемы счетчика, примем, что он состоит из восьми разрядов. Q1 ‘:=‘ ‘ЕСЛИ’ Р0 V Z0 ‘ТО’ IQ1 ‘ИНАЧЕ’ Q1; P1 ‘:=‘ Q1 * P0; Z
Q [1:8] ’:=‘ ‘ЕСЛИ’ ТЗн * X0 ‘ТО’ Q[1:8] + 1 ‘ИНЕСЛИ’ IТЗн * X0 ‘ТО‘ Q[1:8] – 1 ‘ИНАЧЕ’ Q [1:8];
Рис. 10.12. УГО реверсивного счетчика
Дешифраторы Дешифратор - ФУ, который предназначен для декодирования (определения) состояния регистров или счетчиков, т.е. преобразования двоичного или иного кода в единичный позиционный код. На рис.10.15 показано объединение регистра и дешифратора в одну схему.
Рис. 10.15. Объединение регистра и дешифратора Составим МОДИС-описание логической схемы дешифратора для трехразрядной двоичной переменной X. X = {X0, X1...X3} D0 ‘:=‘ IX0 * IX1 * IX2 * IX3; D1 ‘:=‘ X0 * IX1 * IX2 * IX3; ... D15 ‘:=‘ X0 * X1 * X2 * X3; Дешифраторы бывают одноступенчатые (рис.10.16), двухступенчатые и многоступенчатые. 10.4.1. Одноступенчатый дешифратор
Рис. 10.16. Принципиальная схема одноступенчатого дешифратора Сложность логической схемы (ЛС) дешифратора оценивается по суммарному количеству входов всех логических элементов, входящих в его состав. Для одноступенчатого дешифратора M = n n –количество разрядов в двоичном коде. Если n =10, то M = 10 ∙1024 = 104. 10.4.2. Двухступенчатый дешифратор Допустим, что на входе дешифратора функция шести переменных
Запишем логическое выражение для одного из выходов дешифратора в виде конъюнкции от шести переменных X [0: 5]. Затем с помощью круглых скобок представим его в виде произведения двух конъюнкций от трех переменных. Таким же образом нужно записать выражения для всех остальных выходов дешифратора
Первая конъюнкция в круглых скобка представляет собой один из выходов одноступенчатого дешифратора функции трех переменных X [0:2], вторая конъюнкция - соответственно от переменных X [3:5]. Произведение двух этих конъюнкций в круглых скобках представляет собой вторую ступень дешифратора. Соответствующая логическая схема двухступенчатого дешифратора представлена в виде фрагмента на рис. 10.17. Подсчитаем суммарное количество входов логических схем для двухступенчатого дешифратора. На рис. 10.17 имеются два дешифратора первой ступени, каждый из них на три входных
переменных, и один дешифратор второй ступени, который объединяет оба дешифратора первой ступени. М2ст = (n/2*2*n/2)*2+2*2n = n*2n/2 + 2n+1
Рис. 10.17. Двухступенчатый дешифратор При очень большом количестве разрядов строятся многоступенчатые дешифраторы.
Качество дешифраторов характеризуется, кроме того, быстродействием.
Временное запаздывание одноступенчатого дешифратора При проектировании дешифратора необходимо выбрать некоторый оптимум между сложностью аппаратуры и временной задержкой, которую он вносит в систему. Аналогично можно построить и двоично-десятичный дешифратор (рис.10.18).
Рис. 10.18. УГО двоично-десятичного дешифратора
Мультиплексор Мультиплексор - ФУ, обеспечивающий передачу данных с одного из нескольких входов на выход в зависимости от значения управляющего сигнала.
Рис. 10.21. УГО мультиплексора На рис. 10.21 показано УГО, а на рис. 10.22 представлена логическая схема мультиплексора, а также обозначены его входы. {X1÷ Xn } -информационные входы {V1÷ Vk } - управляющие входы F ’:=‘ ‘ЕСЛИ’ D1 ‘ТО’ X1 ‘ИНЕСЛИ’ D2 ‘ТО’ X2 .... ‘ИНЕСЛИ’ Dn ‘ТО’ Xn ‘ИНАЧЕ’ 0;
Рис. 10.22.Функциональная схема мультиплексора
Демультиплексор Демультиплексор – ФУ, который обеспечивает передачу входного сигнала на один из нескольких выходов в зависимости от значения управляющего сигнала. Функциональная схема и УГО демультиплексора показаны на рис.10.23 и 10.24. Мультиплексор и демультиплексор используются в составе различных цифровых устройств для преобразования параллельных кодов в последовательные и обратно.
Рис. 10.23. Функциональная схема демультиплексора
Рис. 10.24. УГО демультиплексора Полусумматор одноразрядный Полусумматор одноразрядный – это логическая схема, обеспечивающая суммирование двух двоичных цифр. а, b – слагаемые
М2(a,b) - сумма по модулю 2 q – перенос q = а & b. Таблица 10.4
В табл. 10.4 представлена ТИ полусумматора, и в соответствии с этой таблицей составлены логические функции для полусуммы (П) и переноса (q).
Также показаны УГО сумматора по модулю 2 (рис.10.25) и УГО полусумматора, выполняющего функцию сложения двух двоичных
цифр (рис. 10.26). Как следует из табл. 10.4, если а = в, то М2(a,b)=0, т.е. сумма четна. Если же а≠в, то М2(a,b)=1, т.е. нечетна.
Рис. 10.26. УГО полусумматора Могут быть построены логические схемы полусумматоров комбинационного типа (рис. 10.27) и накапливающего типа (рис. 10.28).
Рис. 10.27. Логическая схема комбинационного полусумматора Накапливающий полусумматор строится на основе триггера со счетным входом. На рис. 10.28 триггер выполняет функцию полусуммирования. Если на счетный вход подать в после-довательном коде многоразрядную двоичную переменную А = f (a1, a2, a13,… ak), то подсчитывается четность числа единиц в этой переменной.
Рис. 10.28. Логическая схема накапливающего сумматора Системы цифровых элементов. Состав. Система цифровых элементов – это совокупность логических, запоминающих и вспомогательных элементов, согласующихся между собой и имеющих единое конструктивное выполнение. Системы цифровых элементов (СЦЭ) классифицируются по двум признакам: типам связи между элементами в схеме; типам приборов, которые используются для реализации тех или иных функций в составе элементов. В зависимости от вида связи различают следующие системы цифровых элементов: потенциальные СЦЭ - отличаются тем, что при построении схемы разрешены только потенциальные связи (рис. 4.1);
Рис. 4.1. Схема связей потенциальных ЛЭ импульсные СЦЭ – при построении схем разрешены только импульсные связи (рис. 4.2);
Рис. 4.2. Схема связей импульсных ЛЭ импульсно- потенциальные СЦЭ, в которых разрешены и те, и другие связи (рис.4.3).
Рис. 4.3. Схема связей импульсно- потенциальных ЛЭ Согласование цифровых элементов означает использование одних и тех же источников питания и одинаковых уровней логических сигналов. Вспомогательными элементами являются различные типы усилителей, формирователей сигналов, схемы согласования и индикаторы. Эти схемы рассматриваются в курсе «Электроника». В настоящее время используют в основном только потенциальные системы элементов. Потенциальные элементы обеспечивают более высокую надежность при передаче информации, а также являются предпочтительными при использовании интегральных технологий, так как в их схемах отсутствуют емкости и индуктивности.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 566; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.158.29 (0.011 с.) |



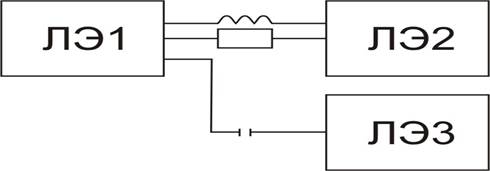



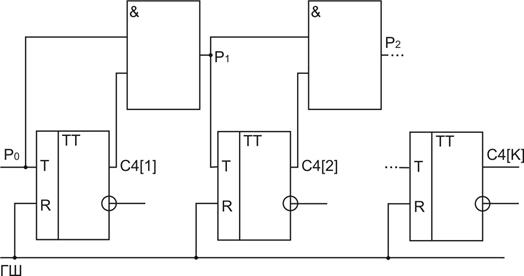
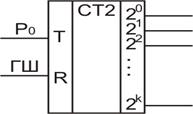



 Рис. 10.11. Реверсивный счетчик
Рис. 10.11. Реверсивный счетчик ‘:=’ IQ1 * Z
‘:=’ IQ1 * Z  ;
;


 - количество входов ЛС.
- количество входов ЛС.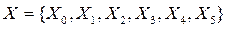 .
. .
.


 .
. - задержка логического элемента “И”.
- задержка логического элемента “И”. , двухступенчатого -
, двухступенчатого - 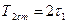 .
.





 П = а & b V a & b = а
П = а & b V a & b = а  b = М2(a,b)
b = М2(a,b)
 Рис. 10.25. УГО сумматора по модулю 2
Рис. 10.25. УГО сумматора по модулю 2





