
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Счетчик с групповым переносомСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Для повышения быстродействия счетчиков с большим количеством разрядов применяют схемы с групповым переносом. В схеме на рис. 10.10 принято, что внутри группы [1: К] разрядов перенос организован последовательным способом, а между группами – параллельным. Полное количество разрядов в счетчике n =КL, где К – число разрядов в группе, L- количество групп. τp – время формирования группового переноса или переноса между разрядами. Время регистрации счетчика Трег = τp (K + L – 1).
Рис. 10.10. Двоичный счетчик с групповым переносом
Двухтактный регистр сдвига вправо на R–S- триггерах Схема на рис. 10.1 построена на синхронизируемых R–S- триггерах. Каждый разряд регистра сдвига включает в себя два одноступенчатых R–S- триггера. Режим сдвига может также рассматриваться как процесс ввода информации в регистр в последовательном коде парафазным способом через входные контакты Р[0]. В данной схеме, кроме того, предусмотрен ввод информации в параллельном коде однофазным способом. Для этой цели сначала все триггеры устанавливаются сигналом ГШ в нуль, а затем сигналом ПР устанавливаются в “1” в соответствии со значением кода W[1:2].
Рис. 10.1.Схема регистра сдвига вправо на один разряд Составим МОДИС- модель для схемы на рис.10.1. Описание переменных: ‘ЗАВИСИМ’ Q [1:2], РГ [1:2]; ‘ИНЕЗАВ‘ ГШ, СДВ, ПР; ‘ПНЕЗАВ’ W[1:2], РГ[0]; Описание схемы: Q [1] ’:=‘ ‘ЕСЛИ’ (ПР * W[1] + СДВ + ГШ) > 1 ’ТО’ ↑ ‘ИНЕСЛИ’ ГШ ‘ТО’ 0 ‘ИНЕСЛИ’ ПР * W[1] ‘ТО’ 1 ‘ИНЕСЛИ’ СДВ ‘ТО’ РГ[0] ‘ИНАЧЕ’ Q[1]; РГ [1] ’:=‘ ‘ЕСЛИ’ IСДВ ‘ТО’ Q[1] ‘ИНАЧЕ’ РГ[1]; РГ [1:2] ‘:=‘ ‘ЕСЛИ’ ГШ ‘ТО’ 0 ‘ИНЕСЛИ’ ПР ‘ТО’ W[1:2] ‘ИНЕСЛИ’ СДВ ‘ТО’ ‘СДВПР’ 1 ‘ИНАЧЕ’ РГ [1:2];
Триггеры первой ступени Q[1:2] управляются передними фронтами импульсов сдвига, а триггеры второй ступени РГ[1:2] - задними фронтами этих же импульсов (рис.10.2).
Рис. 10.3. УГО регистра сдвига на двухтактных R-S- триггерах Поэтому, как видно из временной диаграммы, моменты срабатывания триггеров 2-й ступени запаздывают на 0,5 такта. На схеме (рис.10.1) сдвиг информации реализуется двухфазным способом. УГО регистра сдвига показано на рис. 10.3.
Реверсивный счетчик Реверсивный счетчик обеспечивает, как суммирование, так и вычитание импульсов из содержимого счетчика. Существуют две основные структуры реверсивных счетчиков: 1) на вход схемы подается одна последовательность входных импульсов, но в каждый момент времени известен ее знак или режим работы счетчика, 2) на вход реверсивного счетчика поступают две последовательности импульсов с разными знаками. Схема, представленная на рис. 10.11, соответствует первой структуре. На вход схемы поступает одна последовательность сигналов. Триггер знака ТЗн определяет режим работы счетчика.
В режиме сложения формируется входной сигнал с положительным знаком и последовательность переносов P0 ’:=‘ ТЗн * X0; в режиме вычитания - последовательность заемов Z0 ‘:=‘ IТЗн * X0; таким образом, на входе первого триггера Q1 появляются две последовательности сигналов с разными знаками, что соответствует второй структуре. На рис.10.12 показано УГО реверсивного счетчика этого типа. Составим МОДИС-описание схемы счетчика, примем, что он состоит из восьми разрядов. Q1 ‘:=‘ ‘ЕСЛИ’ Р0 V Z0 ‘ТО’ IQ1 ‘ИНАЧЕ’ Q1; P1 ‘:=‘ Q1 * P0; Z
Q [1:8] ’:=‘ ‘ЕСЛИ’ ТЗн * X0 ‘ТО’ Q[1:8] + 1 ‘ИНЕСЛИ’ IТЗн * X0 ‘ТО‘ Q[1:8] – 1 ‘ИНАЧЕ’ Q [1:8];
Рис. 10.12. УГО реверсивного счетчика
Дешифраторы Дешифратор - ФУ, который предназначен для декодирования (определения) состояния регистров или счетчиков, т.е. преобразования двоичного или иного кода в единичный позиционный код. На рис.10.15 показано объединение регистра и дешифратора в одну схему.
Рис. 10.15. Объединение регистра и дешифратора Составим МОДИС-описание логической схемы дешифратора для трехразрядной двоичной переменной X. X = {X0, X1...X3} D0 ‘:=‘ IX0 * IX1 * IX2 * IX3; D1 ‘:=‘ X0 * IX1 * IX2 * IX3; ... D15 ‘:=‘ X0 * X1 * X2 * X3; Дешифраторы бывают одноступенчатые (рис.10.16), двухступенчатые и многоступенчатые. 10.4.1. Одноступенчатый дешифратор
Рис. 10.16. Принципиальная схема одноступенчатого дешифратора Сложность логической схемы (ЛС) дешифратора оценивается по суммарному количеству входов всех логических элементов, входящих в его состав. Для одноступенчатого дешифратора M = n n –количество разрядов в двоичном коде. Если n =10, то M = 10 ∙1024 = 104. 10.4.2. Двухступенчатый дешифратор Допустим, что на входе дешифратора функция шести переменных
Запишем логическое выражение для одного из выходов дешифратора в виде конъюнкции от шести переменных X [0: 5]. Затем с помощью круглых скобок представим его в виде произведения двух конъюнкций от трех переменных. Таким же образом нужно записать выражения для всех остальных выходов дешифратора
Первая конъюнкция в круглых скобка представляет собой один из выходов одноступенчатого дешифратора функции трех переменных X [0:2], вторая конъюнкция - соответственно от переменных X [3:5]. Произведение двух этих конъюнкций в круглых скобках представляет собой вторую ступень дешифратора. Соответствующая логическая схема двухступенчатого дешифратора представлена в виде фрагмента на рис. 10.17. Подсчитаем суммарное количество входов логических схем для двухступенчатого дешифратора. На рис. 10.17 имеются два дешифратора первой ступени, каждый из них на три входных
переменных, и один дешифратор второй ступени, который объединяет оба дешифратора первой ступени. М2ст = (n/2*2*n/2)*2+2*2n = n*2n/2 + 2n+1
Рис. 10.17. Двухступенчатый дешифратор При очень большом количестве разрядов строятся многоступенчатые дешифраторы.
Качество дешифраторов характеризуется, кроме того, быстродействием.
Временное запаздывание одноступенчатого дешифратора При проектировании дешифратора необходимо выбрать некоторый оптимум между сложностью аппаратуры и временной задержкой, которую он вносит в систему. Аналогично можно построить и двоично-десятичный дешифратор (рис.10.18).
Рис. 10.18. УГО двоично-десятичного дешифратора
Мультиплексор Мультиплексор - ФУ, обеспечивающий передачу данных с одного из нескольких входов на выход в зависимости от значения управляющего сигнала.
Рис. 10.21. УГО мультиплексора На рис. 10.21 показано УГО, а на рис. 10.22 представлена логическая схема мультиплексора, а также обозначены его входы. {X1÷ Xn } -информационные входы {V1÷ Vk } - управляющие входы F ’:=‘ ‘ЕСЛИ’ D1 ‘ТО’ X1 ‘ИНЕСЛИ’ D2 ‘ТО’ X2 .... ‘ИНЕСЛИ’ Dn ‘ТО’ Xn ‘ИНАЧЕ’ 0;
Рис. 10.22.Функциональная схема мультиплексора
Демультиплексор Демультиплексор – ФУ, который обеспечивает передачу входного сигнала на один из нескольких выходов в зависимости от значения управляющего сигнала. Функциональная схема и УГО демультиплексора показаны на рис.10.23 и 10.24. Мультиплексор и демультиплексор используются в составе различных цифровых устройств для преобразования параллельных кодов в последовательные и обратно.
Рис. 10.23. Функциональная схема демультиплексора
Рис. 10.24. УГО демультиплексора Полусумматор одноразрядный Полусумматор одноразрядный – это логическая схема, обеспечивающая суммирование двух двоичных цифр. а, b – слагаемые
М2(a,b) - сумма по модулю 2 q – перенос q = а & b. Таблица 10.4
В табл. 10.4 представлена ТИ полусумматора, и в соответствии с этой таблицей составлены логические функции для полусуммы (П) и переноса (q).
Также показаны УГО сумматора по модулю 2 (рис.10.25) и УГО полусумматора, выполняющего функцию сложения двух двоичных
цифр (рис. 10.26). Как следует из табл. 10.4, если а = в, то М2(a,b)=0, т.е. сумма четна. Если же а≠в, то М2(a,b)=1, т.е. нечетна.
Рис. 10.26. УГО полусумматора Могут быть построены логические схемы полусумматоров комбинационного типа (рис. 10.27) и накапливающего типа (рис. 10.28).
Рис. 10.27. Логическая схема комбинационного полусумматора Накапливающий полусумматор строится на основе триггера со счетным входом. На рис. 10.28 триггер выполняет функцию полусуммирования. Если на счетный вход подать в после-довательном коде многоразрядную двоичную переменную А = f (a1, a2, a13,… ak), то подсчитывается четность числа единиц в этой переменной.
Рис. 10.28. Логическая схема накапливающего сумматора
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 1125; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.007 с.) |




 Рис. 10.2. Временная диаграмма работы регистра сдвига
Рис. 10.2. Временная диаграмма работы регистра сдвига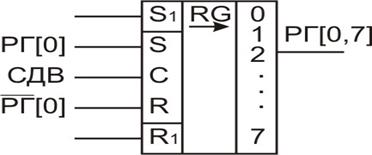

 ‘:=’ IQ1 * Z
‘:=’ IQ1 * Z  ;
;


 - количество входов ЛС.
- количество входов ЛС.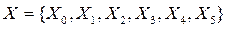 .
. .
.


 .
. - задержка логического элемента “И”.
- задержка логического элемента “И”. , двухступенчатого -
, двухступенчатого - 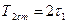 .
.





 П = а & b V a & b = а
П = а & b V a & b = а  b = М2(a,b)
b = М2(a,b)
 Рис. 10.25. УГО сумматора по модулю 2
Рис. 10.25. УГО сумматора по модулю 2





