Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ:  Археология Биология Генетика География Информатика История Логика Маркетинг Математика Менеджмент Механика Педагогика Религия Социология Технологии Физика Философия Финансы Химия ЭкологияТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Счетчик Джонсона с самовосстановлением. ⇐ ПредыдущаяСтр 6 из 6
Введем второе покрытие, надеясь, что оно обеспечит само восстановление.
Если в цикле запрещенных состояний изменить 0 на 1 напротив кода 1001, то из любого запрещенного состояния, по крайней мере, через 8 тактов счетчик вернется в разрешенное. Для упрощения схемы можно так же поменять 0 на 1 напротив комбинации 1011. Для счетчика Джонсона существует обобщенная формула:
Например:
Для упрощения схемы коррекции её можно распределить между разрядами регистра. Пример счетчика:
Счетчик Джонсона Счетчик Джонсона без самовосстановления: с самовосстановлением:
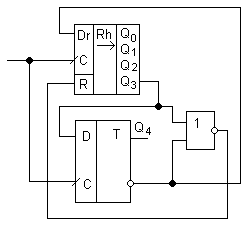
Иной подход к восстанавливаемости работоспособности счетчика Джонсона. В любой запрещенной комбинации встречаются 0 и 1, следовательно, после какого-либо количества сдвигов мы получим в старших разрядах 10. При этом среди разрешенных комбинаций 10 в старших разрядах имеет лишь состояние 1000…00, следовательно, выявив 10 в старших разрядах можно младшие разряды сбросить, на этом и строится принцип коррекции.
Если Q4=1 и Q3=0, то на выходе элемента «ИЛИ-НЕ» - 1, и она сбрасывает содержимое регистра. Получаем разрешенную комбинацию 1000…0.
Удаление лишних состояний из двоичного счетчика.
За основу берут двоичный счетчик и удаляют лишние состояния. В данном методе путем блокировки переносов в двоичном счетчике добиваются заданного модуля счета. Это осуществляется путем формального синтеза, имеющего следующие этапы: Приводятся таблицы переходов и функции возбуждения. Осуществляется тем или иным образом минимизация функции возбуждения (например, с помощью карт Карно). Строится схема. Если при минимизации получают КНФ или ДНФ, то полученный счетчик будем иметь с параллельным переносом. Если при получении функции возбуждения старших разрядов используют значение функции младших разрядов, то получают схему со сквозным переносом. Пример: Двоично-десятичный счетчик на JK-триггерах.
После таблицы минимизируем, например, с помощью карт Карно, и получаем следующий результат:
Сигнал
В заключении необходимо проверить поведение счетчика в запрещенных комбинациях: Счетчик из всех запрещенных комбинаций выходит в разрешенные, т.е. обладает самовосстанавливаемостью.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 458; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.156.200 (0.008 с.) |
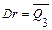
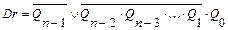
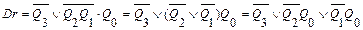
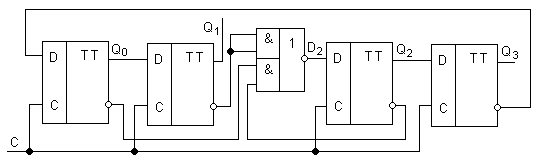
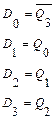
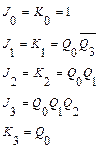
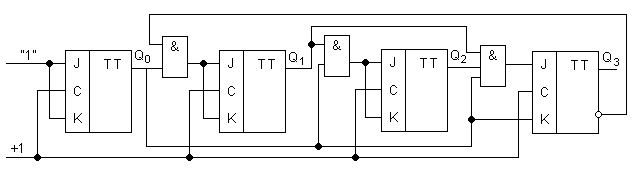
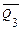блокирует распространение переноса от Q0 к Q1, в остальном схема подобна двоичному счетчику с параллельным переносом. От 0000 до кода 0111 счетчик считает как обычный двоичный, т.к. 
