Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Счетчики с произвольным модулем счета (или не двоичные).Содержание книги Поиск на нашем сайте
Не двоичные счетчики – это счетчики, у которых M≠2n, где n – число разрядов, а М – число состояний. Существует два подхода к реализации таких счетчиков: 1) За основу берут сразу не двоичный счетчик. 2) За основу берут двоичный счетчик и удаляют лишние состояния. К не двоичным счетчикам относят: полиноминальные, счетчики Джонсона и др. Из двоичных счетчиков не двоичные получают методом блокировки переноса или методом принудительного насчета. Рассмотрим не двоичные счетчики на примере двоично-десятичного счетчика (модуль счета 10). В двоично-десятичном коде одна десятичная цифра представлена четырьмя двоичными разрядами. Эти четыре разряда называют тетрадой или декадой.
За основу берут сразу не двоичный счетчик. Полиноминальные счетчики. Полиноминальными счетчиками называют пересчетные схемы, получаемые на основе сдвигающих регистров, в которые заведены обратные связи через сумматоры по модулю 2. Часто используют для получения псевдослучайной последовательности чисел. Сумматор по модулю 2:
Условное графическое обозначение:
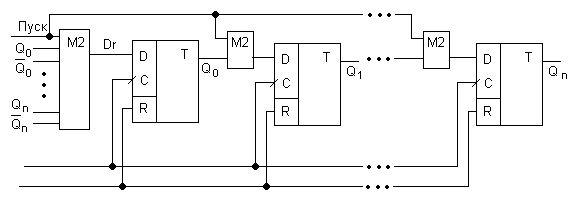
Двухвходовые сумматоры на входе D используются лишь в начальный момент для установки начального кода. На вход триггера Q0 устанавливается многовходовой сумматор, на вход которого заводят прямые или инверсные выходы триггеров. Количество разрядов которые заводят на вход М2 не регламентируются (может быть 1, а может и n+1). Если на вход М2 заводятся только прямые значения Q или четное количество инверсных, то счетчику обязательно требуется сигнал «Пуск». Если число инверсных входов не четно, то сигнал «Пуск» не обязателен, а тогда не нужны и двухвходовые сумматоры по модулю 2.
Многовходовой сумматор дополнительно может быть установлен и на входы других разрядов, не только Q0. В стандартном полиноминальном счетчике на вход многовходового сумматора М2 заводят только прямые значения Q и начальная установка такого счетчика состоит из двух этапов:
Пример: Стандартный счетчик на 7 состояний.
М=7 (модуль счета)
М=7 (модуль счета) Если полиноминальный счетчик имеет 2n-1 состояний и одно состояние – начальное устойчивое, то его называют генератор псевдослучайной последовательности.
Счетчики Джонсона Код Джонсона.
Каждое состояние кода Джонсона однозначно определяется по двум разрядам, следовательно, чтобы иметь дешифратор Джонсона на 2n выходов необходимо воспользоваться n двухвходовыми элементами. Два соседних состояния кода Джонсона разнятся лишь в одном разряде, следовательно, при работе счетчика всегда переключается только один разряд. И только один разряд может внести помеху из-за переключения и потребляет динамическую мощность. В виду последнего счетчик в коде Джонсона можно строить на неограниченное число разрядов. При наличии n триггеров получаем 2n состояний – четное число. Если необходимо получить нечетное число состояний удаляется состояние содержащее все 1.
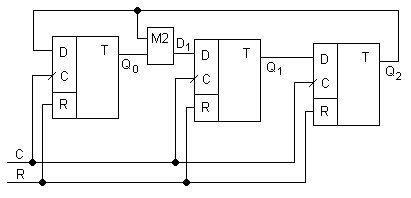
Схемотехнически счетчик Джонсона представляет собой сдвигающий регистр с перекрестной обратной связью.
2*4=8 состояний (4 – число триггеров)
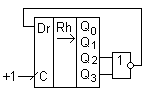
Схема на нечетное количество состояний:
Счетчик не обладает самовосстанавливаемостью, если он попадет в любое запрещенное состояние, то он из него не выйдет.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 366; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.167.138 (0.006 с.) |

 запрещенные
запрещенные


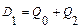
 0
0