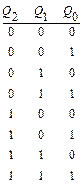Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Параметры, характеризующие динамические свойства счетчиковСодержание книги
Поиск на нашем сайте
1) Время установления или время регистрации:
2) Время задержки переноса:
3) Минимальная длительность входного сигнала:
4) Минимальный период входного сигнала:
5) Максимальная частота работы счетчика:
Условное графическое обозначение: Синхронный Асинхронный
CI, C0 – вход и выход переноса. Остальные входы и выходы аналогичны регистрам. СТ2 – двоичный счетчик. СТ2-10 – двоично-десятичный счетчик.
Двоичный счетчик с последовательным переносом.
Схема функционирует как суммирующий счетчик. Однако из-за задержек срабатывания триггеров наряду с правильными показаниями счетчика встречаются и ложные. Для получения правильных значений результат необходимо считывать после окончания всех переходных процессов. Для этого иногда вводят специальные стробирующие импульсы.
Параметры:
В двоичном счетчике период выходного сигнала каждого разряда в два раза длиннее периода предыдущего разряда. По этому счетчик используется в качестве делителя частоты. Для получения вычитающего счетчика на вход Т триггера необходимо завести прямой выход (а не инверсный) предыдущего разряда. Особенности схемы: · Низкие аппаратурные затраты. · Низкое быстродействие в качестве счетчика. · Схема имеет наивысшее быстродействие в качестве делителя частоты.
Счетчик с параллельным переносом.
Из примера видно, что после прибавления 1 результат, сравнивая его с исходным кодом, делится на не изменившуюся часть и изменившуюся. В изменившейся части все разряды инвертированы. Отсюда получаем правило, что прибавление 1 равносильно инвертированию всех младших разрядов счетчика до первого 0 включительно. Выявить комбинацию все 1 в младших разрядах можно с помощью конъюнктора. Таким образом, каждый разряд дополняется конъюнктором, число входов которого равно числу входов младших разрядов.
Параметры:
Схема счетчика имеет максимальное быстродействие, которое не зависит от числа разрядов. Недостаток: дополнительные затраты в виде конъюнкторов, у которых с ростом числа разрядов увеличивается число входов и увеличивается нагрузка на выходы, особенно на первый разряд.
Условное графическое обозначение:
Это асинхронный счетчик
А это уже синхронный счетчик
Условное графическое обозначение:
Счетчик со сквозным переносом.
Параметры:
В литературе данную схему часто называют счетчик с последовательным переносом, однако его параметры отличаются от параметров счетчика с последовательным переносом, ранее нами рассмотренным, что проявляется если
Счетчик с комбинированным (или групповым) переносом. Весь счетчик разбивается на группы. Внутри группы организуют параллельный перенос, между группами перенос сквозной либо последовательный.
Предположим все 12 разрядов счетчика в 0, при поступлении первых импульсов работает только первая группа, т.к. среди Q0, Q1, Q2, Q3 есть хотя бы один 0 и сигнал А равен 0, пока счетчик досчитает до 14. Следующий спад после 14 переводит все разряды первой группы в 1, но к этому времени сигнал «+1» и сигнал А остается в 0. Появление импульса «+1» переведет А в 1, спад же «+1» сбросит все разряды первой группы и сбросит сигнал А. Спад сигнала А увеличит на единицу счетчик второй группы. В результате после числа 15 (01111) получим 16 (10000). Следующий импульс появится на 16-ом периоде «+1». Если вместо элементов «И» на вход «+1» группы завести старший разряд предыдущей группы, то между группами получим последовательный перенос.
Реверсивные счетчики. Существуют два способа построения реверсивных счетчиков: · Основанный на изменении межразрядных связей. · Основанный на обращении кодов.
Построение реверсивного счетчика способом изменения межразрядных связей.
При V=1 верхние конъюнкторы заблокированы. Сигнал с инверсного выхода триггера
Построение реверсивного счетчика способом обращения кода.
Прямые значения Инверсные значения с триггеров с триггеров
Если прямые значения выходов разрядов увеличивается на 1, то их инверсии уменьшаются на 1, следовательно, при выдаче прямого значения разрядов получаем суммирование, а при выдаче инверсного – вычитание. Однако, если в момент смены направления счета, вместо прямого значения выдать инверсное, или наоборот, то момент смены приведет к изменения значения на выходе. Чтобы этого не произошло надо произвести двойную инверсию: 1 – инвертировать содержимое счетчика и 2 – выдать инверсное значение. Данный способ удобен лишь в том случае, если в счетчике имеются обе микрооперации.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 125; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.201.101 (0.008 с.) |

 - интервал от поступления импульса на вход, до появления нового кода на выходе.
- интервал от поступления импульса на вход, до появления нового кода на выходе. - время от появления входного сигнала до появления сигналов на входе всех триггеров.
- время от появления входного сигнала до появления сигналов на входе всех триггеров.



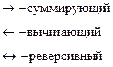
















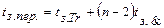


 . Если же
. Если же  , то счетчики с последовательным и сквозным переносом имеют близкие динамические параметры.
, то счетчики с последовательным и сквозным переносом имеют близкие динамические параметры.



 через два инвертора «И-НЕ» поступает на вход Т, получаем схему суммирующего счетчика с последовательным переносом. При V=0 блокируются нижние конъюнкторы и прямой выход триггера через два инвертора «И-НЕ» поступает на вход Т, получаем схему вычитающего счетчика с последовательным переносом.
через два инвертора «И-НЕ» поступает на вход Т, получаем схему суммирующего счетчика с последовательным переносом. При V=0 блокируются нижние конъюнкторы и прямой выход триггера через два инвертора «И-НЕ» поступает на вход Т, получаем схему вычитающего счетчика с последовательным переносом.