Триггер со счетным входом (Т–триггер)

Основной особенностью Т-триггера является то, что при поступлении на его вход очередного импульса триггер изменяет свое состояние на противоположное. Существуют две структуры Т–триггеров: однотактная и двухтактная. Однотактные схемы в настоящее время практически не используются из-за их недостаточной надежности.

На рис. 8.7 представлена логическая схема Т-триггера со счетным входом, построенная на элементной базе “И-ИЛИ-НЕ”. Как видно из схемы, выходы триггера Q связаны со входами обратными связями.

 

Рис. 8.7. Логическая схема двухтактного Т- триггера

Двухтактная схема используется для того, чтобы с помощью обратной связи создать механизм запоминания предыдущего состояния триггера на время переходного процесса при установке триггера первой ступени в противоположное состояние.

УГО Т-триггера показано на рис. 8.9. Как видно из временной диаграммы (рис.8.8), при поступлении очередного импульса на счетный вход триггера его состояние меняется на противо-положное. При этом между моментами срабатывания триггеров первой и второй ступеней имеется временная задержка, равная длительности синхроимпульса. Частота импульсов, поступающих на вход триггера, делится на два, т.е. сам триггер срабатывает в 2 раза реже.

Рис. 8.8. Временная диаграмма работы Т-триггера

 

 

 

 

Рис.8.9. УГО Т- триггера

 

Таблица 8.2

Сt	Q1t+0,5	Qt+1
	Q1t	Qt
	┐Qt	┐Qt

 

В табл. 8.2 представлена таблица переходов триггера со счетным входом. В ней символ “ ┐” обозначает инверсию сигнала Q.

 

 

Универсальный D-триггер (триггер-задержка)

Его особенность в том, что он имеет один информационный вход (название D от Delay). Триггер запоминает (задерживает) информацию, которая поступает по одному информационному каналу. Триггер также называется универсальным, так как на его основе можно построить все другие типы триггеров. Существуют две структуры D-триггера: однотактная и двухтактная.

8.3.1. Однотактный D-триггер

На рис. 8.10 показано УГО однотактного D –триггера. На рис.8.11 представлена логическая схема D -триггера, построенная на ЛЭ типа “ И-НЕ”. Особенность этой схемы состоит в том, что имеется только один информационный вход D.

Рис. 8. 10. УГО однотактного D-триггера

 

Рис. 8.11. Логическая схема однотактного D-триггера

 

 

Таблица 8.3

D	Ct	St	Rt	Qt+1
				Qt
				Qt

В табл. 8.3 дана таблица переходов однотактного D-триггера.

Из этой таблицы видно, что при С =1 на выходе триггера устанавливается состояние, равное значению входа D.

Двухтактный D-триггер

На рис. 8.12 представлена логическая схема двухтактного D -триггера, построенного на элементной базе “И-НЕ”. УГО двухтактного D –триггера представлено на рис. 8.13. Эта схема отличается от двухтактного R-S -триггера тем, что у нее только один информационный вход D.

Рис. 8.12. Логическая схема двухтактного D-триггера

Рис. 8.13. УГО двухтактного D-триггера

 

 

 

Рис.8.14. Т-триггер на основе двухтактного D-триггера

На основе двухтактного D-триггера можно построить Т-триггер, при этом роль счетного входа выполняет вход С (рис.8.14).

 

 

Универсальный JK-триггер

Эта схема называется универсальной потому, что на ее основе можно построить все основные типы триггеров. JK-триггер имеет только двухтактную структуру (рис.8.15). УГО JK –триггера изображено на рис.8.16.

Рис. 8.15. Логическая схема JK –триггера

 

Рис. 8.16. УГО JK –триггера

 

 

Рис. 8.17. Временная диаграмма работы JK –триггера

На рис. 8.15 представлена логическая схема JK –триггера, которая представляет собой двухступенчатую структуру с обратными связями. Так как схема собрана на ЛЭ “И-НЕ”, то в таблице переходов (табл. 8.4) работа триггера рассматривается в условиях положительной логики. Вход J является входом установки в состояние “1”, вход K – входом установки в “0”.

Триггер первой ступени срабатывает по положительному фронту синхроимпульса, а триггер второй ступени управляется инвертированным синхроимпульсом, т.е. срабатывает по отрицательному фронту синхроимпульса через 0.5 такта.

Рассмотрим работу триггера, используя временную диаграмму (рис.8.17). В первом такте синхроимпульс С:=0, оба триггера находятся в нулевом состоянии. Во втором такте C:=1,K:=0, J: =1 и положительным фронтом синхроимпульса уста-

 

навливается триггер Q':=1, а затем через 0,5 такта по заднему фронту это состояние передается во второй триггер Q: =1.

Таблица 8.4

Ct	J	K	Qt+0,5	Qt+1
	x	x	Qt’	Qt
			Qt’	Qt
			┐Qt’	┐Qt

В третьем и четвертом тактах С:=1, J:=1, K:=1 и в соответствии с таблицей истинности дважды устанавливаются в противоположное состояние оба триггера. В третьем такте Q':=0 и Q:=0, а в четвертом такте Q':=1 и Q:=1. В пятом такте J:=0, K:=1 и оба триггера устанавливаются в нуль. Наконец, в последнем такте С:=1, J;=1, K:=1 состояние обоих триггеров снова изменяется на противоположное Q':=1, Q: =1.

 

 

Счетчики

Счетчик – многоразрядный ФУ, предназначенный для подсчета количества импульсов, поступающих на его вход. Схемы счетчиков разнообразны, и их можно классифицировать по нескольким признакам:

1) в зависимости от системы счисления, в которой ведется подсчет числа импульсов, на: а) двоичные; б) двоично-десятичные;

2) по способу организации переноса между разрядами счетчика: а) с последовательным переносом, б) параллельным переносом, в) групповым переносом;

3) в зависимости от арифметической операции, выполняемой счетчиком: а) суммирующие, б) вычитающие, в) реверсивные;

4) по способу управления: а) асинхронные, б) синхронные.

 

 

10.3.1 Счетчик с последовательным переносом

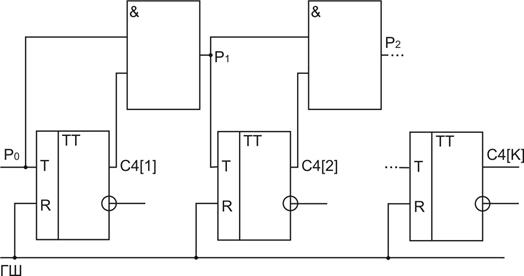
Рис.10.6. Двоичный суммирующий счетчик с последовательным переносом асинхронного типа.

На рис.10.6 и 10.7 приведены схема и УГО двоичного суммирующего счетчика с последовательным переносом асинхронного типа.

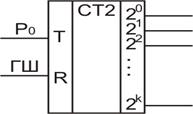
Рис.10.7. УГО счетчика

Ниже показана МОДИС- модель этого счетчика и временная диаграмма работы счетчика (рис.10.8).

Составим МОДИС- модель этого счетчика.

Описание переменных

‘ЗАВИСИМ’ С4 [1:K], Р [1: 2];

‘ИНЕЗАВ’ Р0, ГШ;

Описание схемы

С4 [1] ’:=‘ ‘ЕСЛИ’ ГШ ‘ТО’ 0

‘ИНЕСЛИ’ Р0 ‘ТО’ IC4 [1]

‘ИНАЧЕ’ C4 [1];

Р1 ‘:=‘ C4 [1] * P0

С4 [1:K] ‘:=‘ ‘ЕСЛИ’ ГШ ‘ТО’ 0

‘ИНЕСЛИ’ Р0 ‘ТО’ C4 [1:K]+1

“ИНАЧЕ’ C4 [1:K];

 

 

Рис. 10.8. Временная диаграмма работы счетчика

Каждый разряд счетчика делит частоту поступающих на его вход импульсов на 2. У асинхронного счетчика моменты срабатывания

 

отдельных разрядов счетчика определяются реальными задержками в схемах формирования переноса.

τp - время формирования переноса в одном разряде.

Быстродействие счетчика определяется временем пробега переноса по всем разрядам.

Трег= n * τp – время регистрации – интервал времени от момента поступления на вход счетчика очередного импульса до момента, когда новое значение установится во всех разрядах счетчика.

n –количество разрядов в счетчике.

10.3.2. Счетчик с параллельным переносом

Как следует из рис. 10.9. счетчик является синхронным, так как срабатывание всех триггеров происходит практически одновременно при поступлении на его вход сигнала Р0. Схемы формирования переносов строятся по следующим формулам:

Р1 ‘:=‘ Р0 * Q1;

Р2 ‘:=‘ P1 * Q2 = P0 * Q1 * Q2;

...Pк ‘:=’ P0 * Q1 * Q2 *... * Qk-1; Трег≈ τp.

Счетчики с параллельным переносом обладают наибольшим быстродействием, причем Трег теоретически не зависит от количества разрядов. Однако на практике такие счетчики строятся не более, чем на 8 разрядов.

 

Рис. 10.9. Счетчик с параллельным переносом