
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства неопределённого интегралаСодержание книги
Поиск на нашем сайте
Свойство 1. Производная от неопределённого интеграла равна подынтегральной функции, то есть если
Свойство 2. Дифференциал от неопределённого интеграла равен подынтегральному выражению
Свойство 3. Неопределённый интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной константы
Свойство 4. Неопределённый интеграл от суммы функций равен сумме неопределённых интегралов
Свойство 5. Неопределённый интеграл от разности функций равен соответствующей разности неопределённых интегралов
Свойство 6. Постоянный множитель можно выносить за знак интеграла
Свойство 7. Если
28. Таблица неопределенных интегралов. Интегрирование с помощью тождественных преобразований и свойств неопределенного интеграла на примерах Таблица первообразных (неопределенных интегралов)
Формулы из левого столбца таблицы называют основными первообразными. Формулы из правого столбца основными не являются, но очень часто используются при нахождении неопределенных интегралов. Их можно проверить дифференцированием. Метод непосредственного интегрирования Приведение к табличному виду или метод непосредственного интегрирования. С помощью тождественных преобразований подынтегральной функции интеграл сводится к интегралу, к которому применимы основные правила интегрирования и возможно использование таблицы основных интегралов. Внесение под знак дифференциала В формуле неопределенного интеграла величина
Если нужная функция В общем виде справедливо равенство:
Интегрирование заменой переменной Интегрирование заменой переменной или методом подстановки. Пусть
Определенный интеграл зависит от переменной интегрирования, поэтому если выполнена замена переменных, то обязательно надо вернуться к первоначальной переменной интегрирования. Интегрирование по частям Интегрированием по частям называют интегрирование по формуле
При нахождении функции Использование формулы интегрирования по частям целесообразно в тех случаях, когда дифференцирование упрощает один из сомножителей, в то время как интегрирование не усложняет другой. Интегрирование методом замены переменной. Примеры. Интегрирование по частям в неопределенном интеграле Интегрирование заменой переменной или методом подстановки. Пусть
Определенный интеграл зависит от переменной интегрирования, поэтому если выполнена замена переменных, то обязательно надо вернуться к первоначальной переменной интегрирования. Пример Задание. Найти интеграл Решение. Заменим знаменатель на переменную
Ответ. Интегрирование по частям Интегрированием по частям называют интегрирование по формуле
При нахождении функции Использование формулы интегрирования по частям целесообразно в тех случаях, когда дифференцирование упрощает один из сомножителей, в то время как интегрирование не усложняет другой. Пример Задание. Найти интеграл Решение. В исходном интеграле выделим функции
Ответ.
|
||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 445; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.54.147 (0.006 с.) |

 , то
, то






 означает, что берется дифференциал от переменной
означает, что берется дифференциал от переменной  . Можно использовать некоторые свойства дифференциала, чтобы, усложнив выражение под знаком дифференциала, тем самым упростить нахождение самого интеграла. Для этого используется формула
. Можно использовать некоторые свойства дифференциала, чтобы, усложнив выражение под знаком дифференциала, тем самым упростить нахождение самого интеграла. Для этого используется формула
 отсутствует, иногда ее можно образовать путем алгебраических преобразований.
отсутствует, иногда ее можно образовать путем алгебраических преобразований.
 , где функция
, где функция  имеет непрерывную производную
имеет непрерывную производную  , а между переменными
, а между переменными 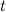 существует взаимно однозначное соответствие. Тогда справедливо равенство
существует взаимно однозначное соответствие. Тогда справедливо равенство

 по ее дифференциалу
по ее дифференциалу  можно брать любое значение постоянной интегрирования
можно брать любое значение постоянной интегрирования  , так как она в конечный результат не входит. Поэтому для удобства будем брать
, так как она в конечный результат не входит. Поэтому для удобства будем брать  .
.




 и
и 





