
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вообще, полное приращение функции не равно сумме частных приращений.Содержание книги
Поиск на нашем сайте
График функции 2-х переменных. Геометрическое место точек, координаты которых удовлетворяют уравнению z= =f(x,y), называется графиком функции двух переменных. Рассмотрим функцию
называется частным приращением функции по переменной Аналогично определяется частное приращение функции
Обозначение частной производной по Частной производной функции
Обозначения: Для нахождения частной производной Аналогично, для нахождения частной производной Каждое из выражений в скобках представляет собой частное приращение функции z. Применим к этим выражениям формулу Лагранжа: Где Обозначим причем Приращения независимых переменных
Первообразная функция и неопределенный интерграл. Свойства неопределенного интеграла Определение первообразной. Первообразной функции f(x) на промежутке (a; b) называется такая функция F(x), что выполняется равенство Если принять во внимание тот факт, что производная от константы С равна нулю, то справедливо равенство
|
|||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 489; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.218.107 (0.009 с.) |

 . Придадим переменной
. Придадим переменной  в точке
в точке 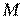 произвольное приращение
произвольное приращение  , оставляя значение переменной
, оставляя значение переменной 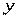 неизменным. Соответствующее приращение функции
неизменным. Соответствующее приращение функции
 .
.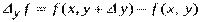 .
. по переменной
по переменной 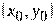 называется конечный предел отношения частного приращения
называется конечный предел отношения частного приращения  функции по переменной
функции по переменной 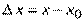 при стремлении к нулю приращения
при стремлении к нулю приращения  :
: .
. ,
,  ,
, 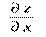 ,
,  .
. по переменной
по переменной  .
.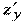 ,
,  ,
,  ,
,  .
.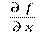 по переменной
по переменной  по переменной
по переменной  постоянной считается переменная
постоянной считается переменная  и
и  . Тогда функция получит приращение,
. Тогда функция получит приращение,  которое называется полным приращением. Запишем
которое называется полным приращением. Запишем  следующим образом:
следующим образом:  (3).
(3). ,
,
 а
а 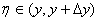 . Если
. Если  и
и  то
то  . Значит, в силу непрерывности частных производных, при
. Значит, в силу непрерывности частных производных, при 
 . Таким образом,
. Таким образом, 
 , где
, где  и
и  бесконечно малые величины. Отсюда:
бесконечно малые величины. Отсюда:  (4).
(4). Тогда
Тогда  , где
, где  . Так как
. Так как  ,
, 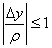 , поэтому
, поэтому  . Значит, при
. Значит, при  также стремиться к нулю. Соотношения
также стремиться к нулю. Соотношения  . Окончательно,
. Окончательно, (5)
(5)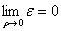 . Формула (5) называется формулой полного приращения функции. Сумма первых двух слагаемых есть выражение линейное относительно
. Формула (5) называется формулой полного приращения функции. Сумма первых двух слагаемых есть выражение линейное относительно  . Линейная часть приращения называется полным дифференциалом функции и обозначается dz.
. Линейная часть приращения называется полным дифференциалом функции и обозначается dz. 
 .
. . Равенство (5) можно переписать в виде:
. Равенство (5) можно переписать в виде:  ,и, с точностью до бесконечно малой высшего порядка относительно
,и, с точностью до бесконечно малой высшего порядка относительно  , причем точность этого равенства тем выше, чем меньше приращения аргументов.
, причем точность этого равенства тем выше, чем меньше приращения аргументов. для любого х из заданного промежутка.
для любого х из заданного промежутка. . Таким образом, функция f(x) имеет множество первообразных F(x)+C, для произвольной константы С, причем эти первообразные отличаются друг от друга на произвольную постоянную величину.
. Таким образом, функция f(x) имеет множество первообразных F(x)+C, для произвольной константы С, причем эти первообразные отличаются друг от друга на произвольную постоянную величину.


