
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциал функции одной переменной и его геометрический смысл. Применение дифференциала к приближенным вычислениямСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для производной используются обозначения
или, учитывая определение 1,
Применение дифференциала в приближенных вычислениях Приращение
где функция
В силу того, что второе слагаемое
А так как в нахождении дифференциал значительно проще, чем приращение функции, то данная формула активно используется на практике. Для приближенного вычисления значения функции применяется следующая формула:
Производные высших порядков функции одной переменной. Примеры Частные производные функции двух переменных z=f(x,y) являются функциями переменных x и y. Поэтому их снова можно дифференцировать. Так как каждую функцию zx/ и zy/ можно дифференцировать по x и y, то производных второго порядка будет четыре. Результат дифференцирования Производные второго порядка можно снова дифференцировать по x или по y. Частная производная n-го порядка, есть первая производная от производной (n-1)-го порядка. Пример. Вычислить Последовательно находим В данном примере сначала дважды дифференцировали по x потом по y. В случае, если частные производные до n-го порядка непрерывны, можно переставлять порядок дифференцирования по отдельным аргументам. Например: Правила вычисления производных высших порядков функции двух переменных справедливы для функции любого числа аргументов. Пример. Используя понятие частных производных n – го порядка, можно определить дифференциал n – го порядка функции z=f(x,y). Определение. Выражение называется дифференциалом n – го порядкафункции z=f(x,y). 1.Предполагается, что функция z=f(x,y) в равенстве (16) имеет непрерывные частные производные до n – го порядка включительно. 2.Выражение (16) задает функцию от переменных 3.Особое значение для приложений имеет дифференциал второго порядка 4. Если Однако в отличие от дифференциала первого порядка ни один из дифференциалов Теорема. Пусть f(x,y) – функция, определенная в некоторой где С помощью формулы (18) исследуется поведение разности
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 602; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.249.76 (0.007 с.) |

 задана на промежутке
задана на промежутке 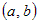 и пусть точка
и пусть точка 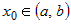 , а число
, а число 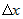 такое, что новая точка
такое, что новая точка 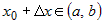 . Приращением
. Приращением 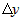 функции
функции 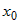 называется разность значений функции в точках
называется разность значений функции в точках 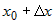 и
и 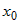 , то есть
, то есть
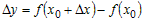 .
.
 Определение 2
Определение 2
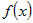 в точке
в точке 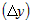 к приращению аргумента
к приращению аргумента 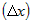 условии, что приращение аргумента стремится к нулю, если этот предел существует и конечен.
условии, что приращение аргумента стремится к нулю, если этот предел существует и конечен.
 , или просто
, или просто  . Итак:
. Итак:
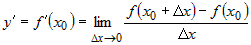
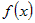 в точке
в точке 
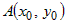 проведем невертикальную касательную
проведем невертикальную касательную 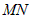 . Через точки
. Через точки  и
и 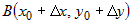 проведем секущую
проведем секущую  (рис.1).
(рис.1).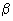 угол, который секущая
угол, который секущая  , а через
, а через 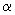 - угол между осью
- угол между осью  в прямоугольном треугольнике
в прямоугольном треугольнике 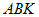 , выполнено равенство:
, выполнено равенство: 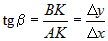 . При
. При 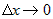 точка
точка 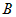 , двигаясь по графику функции
, двигаясь по графику функции 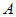 . Тогда
. Тогда , где
, где  - угловой коэффициент касательной. Таким образом, доказано, что
- угловой коэффициент касательной. Таким образом, доказано, что  .
. функции
функции  представимо в виде:
представимо в виде: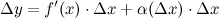
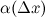 является б.м. функцией при стремлении аргумента
является б.м. функцией при стремлении аргумента  к нулю. Так как
к нулю. Так как  , то
, то
 является бесконечно малым, то им можно пренебречь, а поэтому
является бесконечно малым, то им можно пренебречь, а поэтому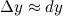
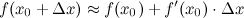
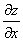 по x обозначается через
по x обозначается через 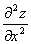 , а результат дифференцирования по y через
, а результат дифференцирования по y через 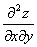 . Производная
. Производная 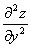 обозначает двукратное дифференцирование функции z=f(x,y) по y.
обозначает двукратное дифференцирование функции z=f(x,y) по y.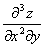 , если z=x3y+ex+2y.
, если z=x3y+ex+2y.
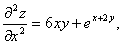


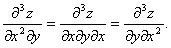
 , Вычислим
, Вычислим  .
.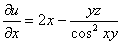 ,
, 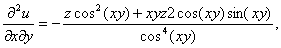

 (16)
(16) При фиксированных
При фиксированных 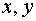 эта функция является однородной функцией степени n переменных
эта функция является однородной функцией степени n переменных  .
.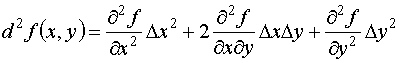 (17)
(17) , поэтому формулу (16) можно записать в виде
, поэтому формулу (16) можно записать в виде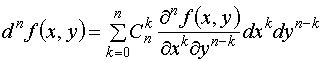 .
.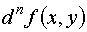 не обладает свойством инвариантности.
не обладает свойством инвариантности. - окрестности точки (x,y) и имеющая непрерывные частные производные по n - го порядка включительно. Тогда справедливо равенство
- окрестности точки (x,y) и имеющая непрерывные частные производные по n - го порядка включительно. Тогда справедливо равенство (18)
(18)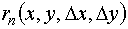 - бесконечно малая более высокого порядка, чем
- бесконечно малая более высокого порядка, чем  при
при 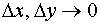 .
.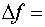
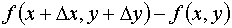 . Разность разбивается на два слагаемых
. Разность разбивается на два слагаемых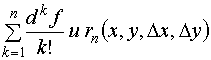 . Зависимость первого из них от
. Зависимость первого из них от  и
и  довольно простая; она описывается многочленом n – й степени от переменных
довольно простая; она описывается многочленом n – й степени от переменных  и
и 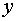 . Второе слагаемое представляет собой величину бесконечно малую более высокого порядка малости, чем
. Второе слагаемое представляет собой величину бесконечно малую более высокого порядка малости, чем 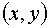 и
и 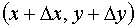 , вследствие чего этим слагаемым во многих задачах можно пренебречь.
, вследствие чего этим слагаемым во многих задачах можно пренебречь.


