Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие множеств. Элементы множества. Обозначение множеств. Пустое множество.Содержание книги
Поиск на нашем сайте
Понятие множеств. Элементы множества. Обозначение множеств. Пустое множество.
Множество - это совокупность объектов, рассматриваемая как одно целое. Понятие множества принимается за основное, т. е. не сводимое к другим понятиям. Объекты, составляющие данное множество, называются его элементами. Основное отношение между элементом a и содержащим его множеством A обозначается так (a есть элемент множества A; или a принадлежит A, или A содержит a). Если a не является элементом множества A, то пишут (a не входит в A, A не содержит a). Множество можно задать указанием всех его элементов, причем в этом случае употребляются фигурные скобки. Так {a, b, c} обозначает множество трех элементов. Аналогичная запись употребляется и в случае бесконечных множеств, причем невыписанные элементы заменяются многоточием. Так, множество натуральных чисел обозначается {1, 2, 3,...}, а множество четных чисел {2, 4, 6,...}, причем под многоточием в первом случае подразумеваются все натуральные числа, а во втором - только четные. Два множества A и B называются равными, если они состоят из одних и тех же элементов, т. е. если каждый элемент множества A принадлежит B и, обратно, каждый элемент B принадлежит A. Тогда пишут A = B. Таким образом, множество однозначно определяется его элементами и не зависит от порядка записи этих элементов. Например, множество из трех элементов a, b, c допускает шесть видов записи: {a, b, c} = {a, c, b} = {b, a, c} = {b, c, a} = {c, a, b} = {c, b, a}. Из соображений формального удобства вводят еще так называемое "пустое множество", а именно, множество, не содержащее ни одного элемента. Его обозначают, иногда символом 0 (совпадение с обозначением числа нуль не ведет к путанице, так как смысл символа каждый раз ясен). Если каждый элемент множества A входит во множество B, то A называется подмножеством B, а B называется надмножеством A. Пишут (A входит в B или A содержится в B, B содержит A). Очевидно, что если и, то A = B. Пустое множество по определению считается подмножеством любого множества. Если каждый элемент множества A входит в B, но множество B содержит хотя бы один элемент, не входящий в A, т. е. если и, то A называется собственным подмножеством B, а B - собственным надмножеством A. В этом случае пишут. Например, запись и означают одно и то же, а именно, что множество A не пусто.
Заметим еще, что надо различать элемент a и множество {a}, содержащее a в качестве единственного элемента. Такое различие диктуется не только тем, что элемент и множество играют неодинаковую роль (отношение не симметрично), но и необходимостью избежать противоречия. Так, пусть A = {a, b} содержит два элемента. Рассмотрим множество {A}, содержащее своим единственным элементом множество A. Тогда A содержит два элемента, в то время как {A} - лишь один элемент, и потому отождествление этих двух множеств невозможно. Поэтому рекомендуется применять запись, и не пользоваться записью.
Числовые множества. Множество натуральных чисел N включают числа вида 1, 2, 3 и т.д., которые используются для счёта предметов. Множество целых чисел Z состоят из натуральных чисел 1, 2, 3,..., числа 0 и чисел, противоположных к натуральным: -1, -2, -3,.... Множество рациональных чисел Q включают в себя выше перечисленные множества и числа вида m/n, где m и n целые числа. Рациональные числа могут быть записаны в виде конечных или бесконечных периодических десятичных дробей. К множеству иррациональных чисел I относятся числа, которые представляются в зиде конечных десятичных дробей или в виде бесконечной периодической дроби. Например: число п. При объединении множества рациональных чисел Q и множества иррациональных чисел Iобразуется множество действительных чисел R. Действительные числа можно изображать в виде точек на числовой прямой. Чтобы задать числовую прямую необходимо отметить на прямой точку, которой будет соответствовать число 0- начало отсчёта, а затем выбрать единичный отрезок и указать положительнео направление. Каждой точке на координатной прямой соответствует число, которое определяется как длина отрезка от начала отсчета до рассматриваемой точки, при этом за единицу измерения принимается единичный отрезок. Это число -координата точки. Если точка взята справа от начала отсчета, то ее координата положительная, а если слева - отрицательная. Например точки О и А имеют координаты 0 и 2, соответственно, что можно записать так: 0(0), А(2). Модуль или абсолютная величина числа х обозначается х. Модуль числа всегда положителен. Определение модуля можно записать с помощью системы:
В геометрическом смысле модуль х представляет собой расстояние отточки А(х) до начала координат.
Правила дифференцирования функции. Таблица производных элементарных функций. Производная - главнейшее понятие математического анализа. Она характеризует изменение функции аргумента x в некоторой точке. При этом она и сама является функцией от аргумента x Производная записывается так: f’(x) или у’. Хотя есть способ решения производных, основанный на определении производной, чтобы не изобретать велосипедов, задачи на вычисление производной чаще решаются с помощью таблицы производных (её вы найдёте в середине этой главы). Операция отыскания производной называется дифференцированием. Упомянутый первый способ (по определению производной) применяется в основном для решения простых задач на физический и геометрический смысл производных и раздел об этом находится в конце данной статьи. А сначала мы будем учиться приводить функции к такому виду, чтобы их производные было возможно найти по таблице производных, чтобы сразу отточить технику дифференцирования, ибо подавляющее большинство задач основано на нахождении табличных производных. Научимся также избегать типичной ошибки при решении производной, причём сделаем это по аналогии с доступным и увлекательным примером из кулинарии. Общий же алгоритм отыскания проиводной, который мы вам предлагаем, очень компактен: 1.Выражение, производную которой требуется найти, нужно разобрать на составные части, подобно тому, как предложение в языке может быть разобрано на подлежащее, сказуемое и другие члены предложения. 2.Поставить полученные составные части в соответствие формулам из таблицы производных (сумма, произведение, частное, степенная функция, сложная функция и др.). 3.Пользуясь таблицей производных, найти производные составных частей выражения и подставить их в выражение. 4.Записать результат. Слово «выражение» здесь только для того используем, чтобы достичь аналогии с предложением речи, которое можно разобрать на составные части. Вообще же говорят «производная функции» (выражение это и есть функция).
Замечание 1. Если функция f непрерывна в каком-либо из концов промежутка возрастания (убывания), то эту точку присоединяют к этому промежутку. Замечание 2. Для решения неравенств f' (х)>0 и f' (х)<0 удобно пользоваться обобщением метода интервалов (теоремой Дарбу): точки, в которых производная равна 0 или не существует, разбивают область определения функции f на промежутки, в каждом из которых f' сохраняет постоянный знак. (Этот факт доказывается в курсах математического анализа.) Знак можно определить, вычислив значение f' в какой-нибудь точке промежутка.
Это условие не очень удобное, так как нужно проверять множество условий и запоминать таблицу, однако если ничего не сказано о производных высших порядках, то это единственный способ найти экстремум функции. 2) Второе достаточное условие Если функция g(x) обладает второй производной 3) Третье достаточное условие
Пусть функция g(x) имеет в некоторой окрестности точки а) Если N - четно, то точка б) Если N - нечетно, то в точке Абсолютный экстремум Наибольшее(наименьшее) значение на сегменте [a;b] непрерывной функции g(x) достигается или в критической точке этой функции(т.е. где производная равна нулю или не существует), или в граничных точках а и b данного сегмента. Асимптомы к графику функции. Примеры. Назовём асимптотами прямые линии, к которым неограниченно приближается график функции, когда точка графика неограниченно удаляется от начала координат. В зависимости от поведения аргумента при этом, различаются два вида асимптот: вертикальные и наклонные. Определение 7.1 Вертикальной асимптотой графика функции Пример 7.1 Рассмотрим функцию
Рис..Вертикальная асимптота функции Производные высших порядков функции одной переменной. Примеры Частные производные функции двух переменных z=f(x,y) являются функциями переменных x и y. Поэтому их снова можно дифференцировать. Так как каждую функцию zx/ и zy/ можно дифференцировать по x и y, то производных второго порядка будет четыре. Результат дифференцирования Производные второго порядка можно снова дифференцировать по x или по y. Частная производная n-го порядка, есть первая производная от производной (n-1)-го порядка. Пример. Вычислить Последовательно находим В данном примере сначала дважды дифференцировали по x потом по y. В случае, если частные производные до n-го порядка непрерывны, можно переставлять порядок дифференцирования по отдельным аргументам. Например: Правила вычисления производных высших порядков функции двух переменных справедливы для функции любого числа аргументов.
Пример. Используя понятие частных производных n – го порядка, можно определить дифференциал n – го порядка функции z=f(x,y). Определение. Выражение называется дифференциалом n – го порядкафункции z=f(x,y). 1.Предполагается, что функция z=f(x,y) в равенстве (16) имеет непрерывные частные производные до n – го порядка включительно. 2.Выражение (16) задает функцию от переменных 3.Особое значение для приложений имеет дифференциал второго порядка 4. Если Однако в отличие от дифференциала первого порядка ни один из дифференциалов Теорема. Пусть f(x,y) – функция, определенная в некоторой где С помощью формулы (18) исследуется поведение разности Определение первообразной. Первообразной функции f(x) на промежутке (a; b) называется такая функция F(x), что выполняется равенство Если принять во внимание тот факт, что производная от константы С равна нулю, то справедливо равенство Интегрирование по частям Интегрированием по частям называют интегрирование по формуле
При нахождении функции Использование формулы интегрирования по частям целесообразно в тех случаях, когда дифференцирование упрощает один из сомножителей, в то время как интегрирование не усложняет другой. Интегрирование методом замены переменной. Примеры. Интегрирование по частям в неопределенном интеграле Интегрирование заменой переменной или методом подстановки. Пусть
Определенный интеграл зависит от переменной интегрирования, поэтому если выполнена замена переменных, то обязательно надо вернуться к первоначальной переменной интегрирования. Пример Задание. Найти интеграл Решение. Заменим знаменатель на переменную
Ответ. Интегрирование по частям Интегрированием по частям называют интегрирование по формуле
При нахождении функции Использование формулы интегрирования по частям целесообразно в тех случаях, когда дифференцирование упрощает один из сомножителей, в то время как интегрирование не усложняет другой. Пример Задание. Найти интеграл Решение. В исходном интеграле выделим функции
Ответ. Несобственные интегралы 1-го рода. Примеры В дальнейшем мы будем обычно иметь дело с несобственными интегралами от неотрицательных функций. Если функция
а) Для сходимости несобственного интеграла
Непосредственно найти такое число
б) Если на луче
В самом деле, из
Но функция
Из доказанного вытекает, что если
Пример 5. Исследуем на сходимость интеграл
Решение. Мы имеем
Пример 6. Исследуем на сходимость интеграл
Решение. Так как Замена переменной в определенном интеграле. Формула интегрирования по частям для определенного интеграла. Примеры Для определенного интеграла справедливы все типы замен, что и для неопределенного интеграла. Таким образом, если с заменами у Вас не очень, следует внимательно ознакомиться с уроком Метод замены в неопределенном интеграле. В этом параграфе нет ничего страшного или сложного. Единственная новизна состоит в вопросе, как поменять пределы интегрирования при замене. В примерах я постараюсь привести такие типы замен, которые еще нигде не встречались на сайте. Пример 5 Вычислить определенный интеграл Главный вопрос здесь вовсе не в определенном интеграле, а в том, как правильно провести замену. Смотрим в таблицу интегралов и прикидываем, на что у нас больше всего похожа подынтегральная функция? Очевидно, что на длинный логарифм: Сначала готовим наш интеграл к замене:
Из вышеуказанных соображений совершенно естественно напрашивается замена:
По сравнению с заменой в неопределенном интеграле у нас добавляется дополнительный этап.
Понятие множеств. Элементы множества. Обозначение множеств. Пустое множество.
Множество - это совокупность объектов, рассматриваемая как одно целое. Понятие множества принимается за основное, т. е. не сводимое к другим понятиям. Объекты, составляющие данное множество, называются его элементами. Основное отношение между элементом a и содержащим его множеством A обозначается так (a есть элемент множества A; или a принадлежит A, или A содержит a). Если a не является элементом множества A, то пишут (a не входит в A, A не содержит a). Множество можно задать указанием всех его элементов, причем в этом случае употребляются фигурные скобки. Так {a, b, c} обозначает множество трех элементов. Аналогичная запись употребляется и в случае бесконечных множеств, причем невыписанные элементы заменяются многоточием. Так, множество натуральных чисел обозначается {1, 2, 3,...}, а множество четных чисел {2, 4, 6,...}, причем под многоточием в первом случае подразумеваются все натуральные числа, а во втором - только четные. Два множества A и B называются равными, если они состоят из одних и тех же элементов, т. е. если каждый элемент множества A принадлежит B и, обратно, каждый элемент B принадлежит A. Тогда пишут A = B. Таким образом, множество однозначно определяется его элементами и не зависит от порядка записи этих элементов. Например, множество из трех элементов a, b, c допускает шесть видов записи: {a, b, c} = {a, c, b} = {b, a, c} = {b, c, a} = {c, a, b} = {c, b, a}. Из соображений формального удобства вводят еще так называемое "пустое множество", а именно, множество, не содержащее ни одного элемента. Его обозначают, иногда символом 0 (совпадение с обозначением числа нуль не ведет к путанице, так как смысл символа каждый раз ясен). Если каждый элемент множества A входит во множество B, то A называется подмножеством B, а B называется надмножеством A. Пишут (A входит в B или A содержится в B, B содержит A). Очевидно, что если и, то A = B. Пустое множество по определению считается подмножеством любого множества. Если каждый элемент множества A входит в B, но множество B содержит хотя бы один элемент, не входящий в A, т. е. если и, то A называется собственным подмножеством B, а B - собственным надмножеством A. В этом случае пишут. Например, запись и означают одно и то же, а именно, что множество A не пусто. Заметим еще, что надо различать элемент a и множество {a}, содержащее a в качестве единственного элемента. Такое различие диктуется не только тем, что элемент и множество играют неодинаковую роль (отношение не симметрично), но и необходимостью избежать противоречия. Так, пусть A = {a, b} содержит два элемента. Рассмотрим множество {A}, содержащее своим единственным элементом множество A. Тогда A содержит два элемента, в то время как {A} - лишь один элемент, и потому отождествление этих двух множеств невозможно. Поэтому рекомендуется применять запись, и не пользоваться записью.
|
|||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 564; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.92.89 (0.011 с.) |



 называется вертикальная прямая
называется вертикальная прямая  , если
, если  или
или 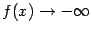 при каком-либо из условий:
при каком-либо из условий: 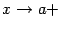 ,
,  ,
,  . Заметим, что мы при этом не требуем, чтобы точка
. Заметим, что мы при этом не требуем, чтобы точка  принадлежала области определения функции
принадлежала области определения функции  , однако она должна быть определена по крайней мере в какой-либо из односторонних окрестностей этой точки:
, однако она должна быть определена по крайней мере в какой-либо из односторонних окрестностей этой точки: 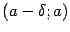 или
или 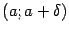 , где
, где 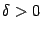 .
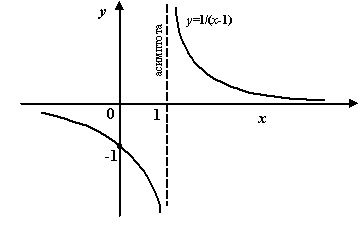
. . График
. График  , поскольку при
, поскольку при  выполняется условие
выполняется условие 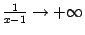 , а также при
, а также при  выполняется условие
выполняется условие  .
.

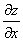 по x обозначается через
по x обозначается через 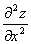 , а результат дифференцирования по y через
, а результат дифференцирования по y через 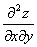 . Производная
. Производная 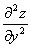 обозначает двукратное дифференцирование функции z=f(x,y) по y.
обозначает двукратное дифференцирование функции z=f(x,y) по y.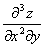 , если z=x3y+ex+2y.
, если z=x3y+ex+2y.
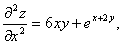


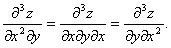
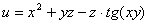 , Вычислим
, Вычислим  .
.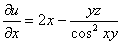 ,
, 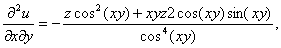

 (16)
(16) При фиксированных
При фиксированных 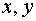 эта функция является однородной функцией степени n переменных
эта функция является однородной функцией степени n переменных  .
.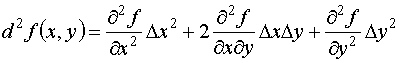 (17)
(17) , поэтому формулу (16) можно записать в виде
, поэтому формулу (16) можно записать в виде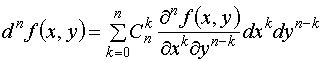 .
.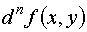 не обладает свойством инвариантности.
не обладает свойством инвариантности.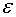 - окрестности точки (x,y) и имеющая непрерывные частные производные по n - го порядка включительно. Тогда справедливо равенство
- окрестности точки (x,y) и имеющая непрерывные частные производные по n - го порядка включительно. Тогда справедливо равенство (18)
(18)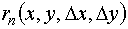 - бесконечно малая более высокого порядка, чем
- бесконечно малая более высокого порядка, чем  при
при 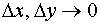 .
.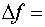
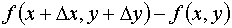 . Разность разбивается на два слагаемых
. Разность разбивается на два слагаемых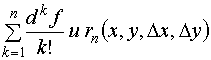 . Зависимость первого из них от
. Зависимость первого из них от  и
и  довольно простая; она описывается многочленом n – й степени от переменных
довольно простая; она описывается многочленом n – й степени от переменных  и
и 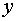 . Второе слагаемое представляет собой величину бесконечно малую более высокого порядка малости, чем
. Второе слагаемое представляет собой величину бесконечно малую более высокого порядка малости, чем 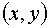 и
и 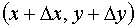 , вследствие чего этим слагаемым во многих задачах можно пренебречь.
, вследствие чего этим слагаемым во многих задачах можно пренебречь. для любого х из заданного промежутка.
для любого х из заданного промежутка. . Таким образом, функция f(x) имеет множество первообразных F(x)+C, для произвольной константы С, причем эти первообразные отличаются друг от друга на произвольную постоянную величину.
. Таким образом, функция f(x) имеет множество первообразных F(x)+C, для произвольной константы С, причем эти первообразные отличаются друг от друга на произвольную постоянную величину.
 по ее дифференциалу
по ее дифференциалу  можно брать любое значение постоянной интегрирования
можно брать любое значение постоянной интегрирования  , так как она в конечный результат не входит. Поэтому для удобства будем брать
, так как она в конечный результат не входит. Поэтому для удобства будем брать  .
. , где функция
, где функция  имеет непрерывную производную
имеет непрерывную производную  , а между переменными
, а между переменными  и
и 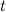 существует взаимно однозначное соответствие. Тогда справедливо равенство
существует взаимно однозначное соответствие. Тогда справедливо равенство





 и
и 


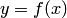 неотрицательна на луче
неотрицательна на луче 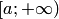 , то функция
, то функция  возрастает на этом луче. Поэтому она имеет предел при
возрастает на этом луче. Поэтому она имеет предел при 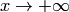 в том и только в том случае, когда ограничена. Отсюда получаем следующее утверждение:
в том и только в том случае, когда ограничена. Отсюда получаем следующее утверждение: от неотрицательной функции
от неотрицательной функции 
 , необходимо и достаточно, чтобы функция
, необходимо и достаточно, чтобы функция  была ограничена, т. е. чтобы нашлось такое число
была ограничена, т. е. чтобы нашлось такое число  , что
, что  для всех
для всех  .
.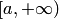 выполняется неравенство
выполняется неравенство  и интеграл
и интеграл  сходится, то сходится и интеграл
сходится, то сходится и интеграл 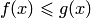 следует, что для любого
следует, что для любого  имеем:
имеем:
 возрастает, и потому ее предел при
возрастает, и потому ее предел при 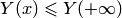 . Поэтому для всех
. Поэтому для всех 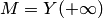 . А тогда на основании предыдущего утверждения интеграл
. А тогда на основании предыдущего утверждения интеграл 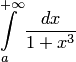 .
. при
при  . Но интеграл
. Но интеграл  сходится (см. пример 4). Поэтому сходится и исходный интеграл.
сходится (см. пример 4). Поэтому сходится и исходный интеграл.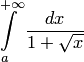 .
. при
при 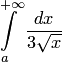 расходится (см. пример 4 при
расходится (см. пример 4 при  ), то расходится и заданный интеграл.
), то расходится и заданный интеграл.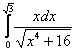
 . Но есть одна неувязочка, в табличном интеграле под корнем
. Но есть одна неувязочка, в табличном интеграле под корнем 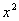 , а в нашем – «икс» в четвёртой степени. Из рассуждений следует и идея замены – неплохо бы нашу четвертую степень как-нибудь превратить в квадрат. Это реально.
, а в нашем – «икс» в четвёртой степени. Из рассуждений следует и идея замены – неплохо бы нашу четвертую степень как-нибудь превратить в квадрат. Это реально.

 .
. подынтегрального выражения, для этого находим дифференциал
подынтегрального выражения, для этого находим дифференциал  :
: