
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функция равна нулю только на наборе (1, 1, 0), поэтомуf(x1 x2 x3)=x1
31. Понятие полинома логической функции (полинома Жегалкина). Понятие линейной логической функции.
Полином Жегалкина — полином(многочлен) над Полином Жегалкина представляет собой сумму по модулю два (операция Исключающее ИЛИ) произведений неинвертированных переменных, а также (если необходимо) константы 1. Формально полином Жегалкина можно представить в виде
или в более формализованном виде как
Примеры полиномов Жегалкина:
По теореме Поста, чтобы система булевых функций была полной, надо, чтобы в ней существовали: 1. Хотя бы одна функция, не сохраняющая 0. 2. Хотя бы одна функция, не сохраняющая 1. 3. Хотя бы одна нелинейная функция. 4. Хотя бы одна немонотонная функция. 5. Хотя бы одна несамодвойственная функция. Этому требованию отвечает система функций По теореме Жегалкина каждая булева функция единственным образом представляется в виде полинома Жегалкина. Теорема доказывается следующим образом. Заметим, что различных булевых функций от n переменных Алгоритм построения полинома Жигалкина: Метод преобразований 1. Построить СДНФ данной булевой функции. 2. Заменить дизъюнкцию в полученной СДНФ на сложение по модулю два. 3. Сделать замену: 4. Раскрыть скобки, пользуясь дистрибутивностью конъюнкции относительно сложения по модулю два: 5. Сократить лишние сомножители и слагаемые, пользуясь эквивалентностями:
Многочлен Жигалкина называется нелинейным, если он содержит конъюкции переменных, а если он не содержит конъюнкции переменных, то он называется линейным. Функция f(x1,x2,..xn) называется линейной, если имеет вид a0⊕a1x1⊕…⊕anxn, и не линейным в противном случае. Чтобы узнать, линейна ли функция, надо выразить ее через полином Жегалкина и посмотреть, не встречается ли там операция &. Если нет, то функция линейна. Для функций от 1 и 2 переменных мы уже приводили формулы, выражающие их через &,
Понятие дизъюнктивной нормальной формы логической функции. Понятие минимальной дизъюнктивной нормальной формы логической функции. Понятие простого импликанта. Понятие сокращенной дизъюнктивной нормальной формы логической функции.
Переменная
Дизъюнкция конечного множества элементарных конъюнкций называется дизъюнктивной нормальной формой(ДНФ). Число элементарных конъюнкций, образующих дизъюнктивную нормальную форму(ДНФ) называется длиной ДНФ. ДНФ содержащая только полные элементарные конъюнкции называется совершенной ДНФ(или СДНФ). Любую логическую формулу А можно представить в виде ДНФ, а затем ДНФ в виде СДНФ.
Преобразование логических функций с целью упрощения их аналитического представления называются минимизацией. Существуют два направления минимизации: 1. Кратчайшая форма записи (цель – минимизировать ранг каждого терма). При этом получаются кратчайшие формы КДНФ, ККНФ, КПНФ. 2. Получение минимальной формы записи (цель – получение минимального числа символов для записи всей функции сразу). При этом следует учесть, что ни один из способов минимизации не универсален. Метод Куайна — способ представления функции в ДНФ или КНФ с минимальным количеством членов и минимальным набором переменных. · на первом этапе осуществляется переход от канонической формы (СДНФ или СКНФ) к так называемой сокращённой форме; · на втором этапе — переход от сокращённой формы к минимальной форме.
|
||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 202; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.006 с.) |
 Úx2
Úx2  =x10Úx20Úx31=
=x10Úx20Úx31=  Ú
Ú 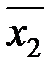 Ú x3
Ú x3 , то есть полином с коэффициентами вида 0 и 1, где в качестве произведения берется конъюнкция, а в качестве сложения исключающее или. Полином был предложен в 1927 годуИ. И. Жегалкиным в качестве удобного средства для представления функций булевой логики.
, то есть полином с коэффициентами вида 0 и 1, где в качестве произведения берется конъюнкция, а в качестве сложения исключающее или. Полином был предложен в 1927 годуИ. И. Жегалкиным в качестве удобного средства для представления функций булевой логики.

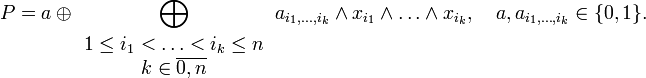

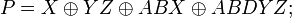
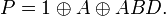
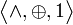 . На её основе и строятся полиномы Жегалкина.
. На её основе и строятся полиномы Жегалкина. штук. При этом конъюнкций вида
штук. При этом конъюнкций вида  существует ровно 2n, так как из n возможных сомножителей каждый или входит в конъюнкцию, или нет. В полиноме у каждой такой конъюнкции стоит 0 или 1, то есть существует
существует ровно 2n, так как из n возможных сомножителей каждый или входит в конъюнкцию, или нет. В полиноме у каждой такой конъюнкции стоит 0 или 1, то есть существует  .
.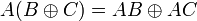 .
.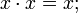

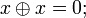

 и константы.
и константы. или
или 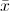 называется литералом (или буквой).
называется литералом (или буквой).


