Определение характеристик стационарного случайного процесса по одной реализации

В исследовании операций нередко приходится встречаться с задачами, где случайный процесс продолжается достаточно долго в одинаковых условиях, и нас как раз интересуют характеристики этого процесса в предельном, установившемся режиме. Например, железнодорожная сортировочная станция работает круглосуточно, и интенсивность потока составов, прибывающих на нее, почти не зависит от времени. В качестве других примеров систем, в которых случайный процесс довольно быстро переходит в устойчивое состояние, можно назвать ЭВМ, линии связи, технические устройства, непрерывно эксплуатируемые и т. п.

О предельном, стационарном режиме и предельных (финальных) вероятностях состояний мы уже говорили в главе 5 (§ 17) в связи с марковскими случайными процессами. Существуют ли они для немарковских процессов? Да, в известных случаях существуют и не зависят от начальных условий. При решении вопроса о том, существуют ли они для данной задачи, можно в первом приближении поступать так: заменить мысленно все потоки событий простейшими; если для этого случая окажется, что финальные вероятности существуют, то они будут существовать и для немарковского процесса. Если это так, то для предельного, стационарного режима все вероятностные характеристики можно определить методом Монте-Карло не по множеству реализации, а всего по одной, но достаточно длинной реализации. В этом случае одна длинная реализация дает такую же информацию о свойствах процесса, что и множество реализации той же общей продолжительности.

 

¹) Этот довод подозрительно напоминает рассуждения г-жи Простаковой («Недоросль» Фонвизина) по поводу ненужности изучения географии: «Да извозчики-то на что? Это их дало. Это и наука-то не дворянская. Дворянин только скажи: повези меня туда, свезут, куда изволишь».

 

 

Пусть в нашем распоряжении — одна длинная реализация стационарного случайного процесса общей продолжительности Т. Тогда интересующие нас вероятности состояний можно найти, как долю времени, которую система проводит в этих состояниях, а средние значения случайных величин получить усреднением не по множеству реализации, а по времени, вдоль peaлизации.

 

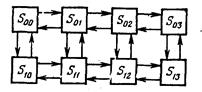
Рис. 24.1

 

Рассмотрим пример. Моделируется методом Монте-Карло работа немарковской одноканальной СМО с очередью. Число мест в очереди ограничено двумя. Заявка, пришедшая в момент, когда оба места в очереди заняты, покидает СМО не обслуженной (получает отказ). Время от времени канал может выходить из строя. Если канал вышел из строя, находившиеся в СМО заявки (как под обслуживанием, так и в очереди), не покидают СМО, а ожидают конца ремонта. Все потоки событий не простейшие, а произвольные рекуррентные. Возможные состояния СМО:

S_0i — канал исправлен, в системе i заявок,

S_1i — канал ремонтируется, в системе i заявок (i = 0, 1, 2,3).

Граф состояний СМО показан на рис. 24.1. Из вида графа заключаем, что финальные вероятности существуют. Предположим, что моделирование работы СМО методом Монте-Карло на большом промежутке времени Т произведено. Требуется найти характеристики эффективности СМО: Р _отк — вероятность того, что заявка покинет СМО не обслуженной, Р _испр — вероятность того, что канал исправен, А — абсолютную пропускную способность СМО, L_сист — среднее число заявок в СМО, L _оч — среднее число заявок в очереди, W _сист и W _оч — среднее время пребывания заявки в системе и в очереди.

Сначала найдем финальные вероятности состояний р₀₀,p₀₁, p₀₂, p₀₃, p₁₀, p₁₁, p₁₂, p₁₃. Для этого нужно вдоль реализации подсчитать суммарное время, которое система находится в каждом из состоянии: T₀₀, Т₀₁, T₀₂, Т₀₃, Т₁₀, T₁₁, Т₁₂, Т₁₃, и разделить каждое из них на время Т. Получим:

 

(i = 0,1,2,3).

 

Вероятность отказа равна вероятности того, что заявка придет в момент, когда в СМО уже находятся три заявки:

 

Р_отк = p₀₃ + p₁₃.

 

Абсолютная пропускная способность равна

А = λ (1 – Р _отк),

где λ — интенсивность потока заявок.

Вероятность того, что канал исправен, получим, суммируя все вероятности, у которых первый индекс равен нулю:

 

P _испр = p ₀₀ + p ₀₁ + p ₀₂ + p ₀₃.

 

Среднее число заявок в СМО подсчитаем, умножая возможные числа заявок в СМО на соответствующие вероятности и складывая:

 

L_сист = 1 (p₀₁ + p₁₁) + 2 (p₀₂ + p₁₂) + 3 (p₀₃ + p₁₃).

 

Это равносильно тому, как если бы мы отметили на оси времени отрезки, на которых в СМО находится 0, 1, 2, 3 заявки и суммарную длительность участков умножили соответственно на 1, 2, 3, сложили и разделили на Т.

Среднее число заявок в очереди L _оч получим, вычитая из L _сист среднее число заявок под обслуживанием (для одноканальной СМО это вероятность того, что канал занят):

Р_зан = 1 - (p₀₀ + p₁₀).

 

Среднее время пребывания заявки в системе и в очереди получим по формуле Литтла:

 

 

На этом мы, заканчиваем краткое наложение метода Монте-Карло, отсылая интересующегося читателя к руководствам [6, 22], где он изложен более полно и где, в частности, рассматривается вопрос о точности статистического моделирования.

 

ГЛАВА 8