Общерекурсивные и частично рекурсивные функции
Вернемся к введенному определению операции минимизации. В общем виде ее можно определять как операцию, применимую к произвольному  местному предикату местному предикату 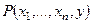 и дающую в результате функцию и дающую в результате функцию  . Значение . Значение  на наборе на наборе  равно наименьшему из таких чисел равно наименьшему из таких чисел  , что высказывание , что высказывание  истинно. Если же наименьшего среди таких чисел не существует, то значение функции истинно. Если же наименьшего среди таких чисел не существует, то значение функции  на наборе на наборе  не определено. Это означает, что операция минимизации может породить частичную, то есть не всюду определенную функцию. не определено. Это означает, что операция минимизации может породить частичную, то есть не всюду определенную функцию.
Операция минимизации является удобным средством для построения обратных функций. Действительно, функция 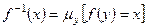 – наименьший – наименьший  , что , что  является обратной для функции является обратной для функции  . .
Пример 7.7. Рассмотрим функцию, полученную с помощью операции минимизации
 , ,
и вычислим  . Полагаем . Полагаем  и, придавая переменной и, придавая переменной  последовательно значения 0,1,2,…, будем вычислять значение суммы последовательно значения 0,1,2,…, будем вычислять значение суммы  . Как только она станет равной 7, то соответствующее значение . Как только она станет равной 7, то соответствующее значение  надо принять за значение надо принять за значение  : :
 , ,
 , ,




Найдем по этому же правилу  : :
 , ,
 , ,
 , … , …
Данный процесс бесконечен, следовательно,  не определено. не определено.
Пример 7.8. С помощью операции минимизации получим частичную функцию, выражающую частное от деления двух чисел из 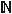  . .
 . .
Теорема 7.7. Если функция  правильно вычислима по Тьюрингу, то функция правильно вычислима по Тьюрингу, то функция  , получающаяся с помощью операции минимизации из , получающаяся с помощью операции минимизации из  , также правильно вычислима. , также правильно вычислима.
Доказательство. Пусть 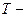 машина Тьюринга, правильно вычисляющая машина Тьюринга, правильно вычисляющая  . Используя ее, сконструируем машину Тьюринга, которая для заданного значения . Используя ее, сконструируем машину Тьюринга, которая для заданного значения  вычисляет последовательно значения вычисляет последовательно значения   , ,  до тех пор, пока не получится до тех пор, пока не получится  . После этого машина Тьюринга должна оставить на ленте число . После этого машина Тьюринга должна оставить на ленте число  , где , где  . Если для любого . Если для любого  будет выполняться будет выполняться  , то МТ не должна останавливаться никогда (это означает, что функция g не определена в точке , то МТ не должна останавливаться никогда (это означает, что функция g не определена в точке  ). ).
Вычисление функции  свяжем с пошаговым циклическим процессом обработки двух блоков на ленте свяжем с пошаговым циклическим процессом обработки двух блоков на ленте  и и  . .

После завершения шага с номером  полагаем, что полагаем, что 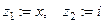 . При выполнении . При выполнении  -го шага вычисляется -го шага вычисляется  и проверяется условие и проверяется условие  . В начале работы на ленте записано: . В начале работы на ленте записано:

 Выполнение шагов Выполнение шагов 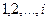 происходит до тех пор, пока не получено равенство происходит до тех пор, пока не получено равенство  . В этом случае процесс вычисление завершается и блок . В этом случае процесс вычисление завершается и блок  затирается, а на ленте остается значение затирается, а на ленте остается значение  в блоке в блоке  как значение как значение  . Иначе . Иначе  увеличивается на единицу. Очевидно, что реализуемы следующие машины Тьюринга: увеличивается на единицу. Очевидно, что реализуемы следующие машины Тьюринга:
 инициализация цикла, запись на ленту блоков инициализация цикла, запись на ленту блоков   . .
 вычисление значения вычисление значения 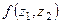 . .
 реализация разветвления по условию реализация разветвления по условию  . .
 вычисление вычисление  . .
 стирает блок стирает блок  и выдаёт и выдаёт  . .
Совместная работа на этих машинах осуществляется согласно схеме, представленной на рис. 7.3 ¡.
Следствие. Всякая частично рекурсивная функция вычислима по Тьюрингу.
Доказательство. Так как операция минимизации сохраняется свойство вычислимости по Тьюрингу, простейшие функции    вычислимы по Тьюрингу, а частично рекурсивная функция получается из простейших с помощью применения конечного числа раз указанных операций, т. е. всякая частично рекурсивная функция вычислима по Тьюрингу ¡. вычислимы по Тьюрингу, а частично рекурсивная функция получается из простейших с помощью применения конечного числа раз указанных операций, т. е. всякая частично рекурсивная функция вычислима по Тьюрингу ¡.
Теорема 7.8. Если функция вычислима по Тьюрингу, то она частично рекурсивна.
Доказательство. Пусть  вычислимая по Тьюрингу функция. Тогда существуют машины Тьюринга, осуществляющая для заданного слова вычислимая по Тьюрингу функция. Тогда существуют машины Тьюринга, осуществляющая для заданного слова  вычисление значения вычисление значения  и остановку в состоянии и остановку в состоянии  . Разобьем доказательство на этапы. . Разобьем доказательство на этапы.
I. В каждый момент времени конфигурация на ленте машины Тьюринга имеет вид  , где , где  слово в алфавите слово в алфавите  записанное на ленте левее обозреваемой в данный момент ячейки; записанное на ленте левее обозреваемой в данный момент ячейки;  состояние, в котором находится в данный момент машина Тьюринга; состояние, в котором находится в данный момент машина Тьюринга;  символ в обозреваемой ячейке; символ в обозреваемой ячейке; 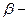 слово в алфавите слово в алфавите  , записанное на ленте правее обозреваемой ячейки. Указанной конфигурации однозначно сопоставляется упорядоченная четверка , записанное на ленте правее обозреваемой ячейки. Указанной конфигурации однозначно сопоставляется упорядоченная четверка  чисел, определяемых следующим образом: чисел, определяемых следующим образом:  ; ;  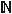  – число, изображаемое цифрами, полученными кодированием символом слова – число, изображаемое цифрами, полученными кодированием символом слова  по правилу: эти символы интерпретируются как по правилу: эти символы интерпретируются как  -значные цифры; -значные цифры;  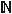  аналогично получается из аналогично получается из  , но при этом читается справа налево, то есть крайняя слева ячейка , но при этом читается справа налево, то есть крайняя слева ячейка  содержит самый младший разряд, а крайняя справа – самый старший. Далее, символу пустой ячейки поставим в соответствие 0; сдвигу вправо содержит самый младший разряд, а крайняя справа – самый старший. Далее, символу пустой ячейки поставим в соответствие 0; сдвигу вправо  сопоставим 1; сдвигу влево сопоставим 1; сдвигу влево  – 2; отсутствию сдвига – 2; отсутствию сдвига  сопоставим 0. Закодируем заключительное состояние сопоставим 0. Закодируем заключительное состояние  символом символом  . Таким образом, алфавит . Таким образом, алфавит  закодируется числовым множеством закодируется числовым множеством  , а алфавит , а алфавит  – числовым множеством – числовым множеством  . .
Например, если 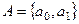 и конфигурация имеет вид и конфигурация имеет вид
 (7.6) (7.6)
то при указанной кодировке ей соответствует упорядоченная четверка натуральных чисел  : :

II. При таком кодировании систему команд машины Тьюринга с алфавитом  и множеством состояний и множеством состояний  можно записать: можно записать:

где 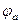 – функция выходов, – функция выходов,  – функция переходов, – функция переходов,  – функция движения. – функция движения.
Так, если в программе машины Тьюринга имеется команда  , то , то    , где , где  , если , если 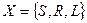 соответственно. Так как соответственно. Так как  заданы на конечном множестве заданы на конечном множестве  , то они являются примитивно рекурсивными. , то они являются примитивно рекурсивными.
III. Таким образом, выполнив одну команду машина Тьюринга преобразует имеющуюся конфигурацию  в новую конфигурацию в новую конфигурацию  . Это означает, что упорядоченной четверке чисел . Это означает, что упорядоченной четверке чисел  , соответствующей конфигурации , соответствующей конфигурации  , однозначно сопоставляется упорядоченная четверка чисел , однозначно сопоставляется упорядоченная четверка чисел  , соответствующая конфигурация , соответствующая конфигурация  . .
Например, при команде  ранее приведенная конфигурация (7.6) перейдет в конфигурацию ранее приведенная конфигурация (7.6) перейдет в конфигурацию  , которой соответствует четверка натуральных чисел , которой соответствует четверка натуральных чисел  . .
В итоге на множестве конфигураций будет задана (вообще говоря, не всюду определенная, то есть частичная) нечисловая функция  , обусловленная данной машиной Тьюринга , обусловленная данной машиной Тьюринга  . Функция . Функция  называется функцией следующего шага. Этой функции соответствует четверка числовых функций следующего шага, то есть называется функцией следующего шага. Этой функции соответствует четверка числовых функций следующего шага, то есть  – числовые функции, каждая из которых зависит от четырех числовых переменных – числовые функции, каждая из которых зависит от четырех числовых переменных  . Очевидно, что . Очевидно, что 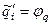 и и  не зависит от не зависит от  , а зависит от , а зависит от  : :   . .
Рассмотрим функцию  . Если в рассматриваемый момент времени головка машины Тьюринга осталась на месте, то есть обозреваемая ячейка не изменилась и . Если в рассматриваемый момент времени головка машины Тьюринга осталась на месте, то есть обозреваемая ячейка не изменилась и  , то , то  . Если головка сдвинулась вправо, то есть . Если головка сдвинулась вправо, то есть  , то степень каждого разряда числа , то степень каждого разряда числа  повысилась на единицу: нулевой разряд стал первым, первый – вторым и т.д., то есть число повысилась на единицу: нулевой разряд стал первым, первый – вторым и т.д., то есть число  увеличилось в увеличилось в  раз (где раз (где  число элементов в алфавите число элементов в алфавите  ): ):  , а в младший (нулевой) разряд помещается та , а в младший (нулевой) разряд помещается та  -ичная цифра, которая соответствует только что вписанному на ленту элементу из -ичная цифра, которая соответствует только что вписанному на ленту элементу из  . Эта цифра равна . Эта цифра равна  . В итоге получим, что при сдвиге вправо . В итоге получим, что при сдвиге вправо   . .
При сдвиге головки влево, то есть при  , степень каждого разряда числа , степень каждого разряда числа  понизится на единицу: первый разряд станет нулевым, второй – первым и т.д., то есть число понизится на единицу: первый разряд станет нулевым, второй – первым и т.д., то есть число  уменьшится в уменьшится в  раз: раз:  . Так как младший (нулевой) разряд оказался как бы «обрубленный», то получилась не частное . Так как младший (нулевой) разряд оказался как бы «обрубленный», то получилась не частное  , а его целая часть , а его целая часть  . Таким образом, для функции . Таким образом, для функции  получено следующее описание: получено следующее описание:

Аналогично можно записать для функции  . При сдвиге вправо (влево) она ведет себя также как функция . При сдвиге вправо (влево) она ведет себя также как функция  при сдвиге влево (вправо): при сдвиге влево (вправо):

Рассмотрим теперь функцию  . Если сдвига не происходит, то . Если сдвига не происходит, то  . Если происходит сдвиг вправо, то машина Тьюринга переходит к обозрению самого левого разряда (это младший разряд) – числа . Если происходит сдвиг вправо, то машина Тьюринга переходит к обозрению самого левого разряда (это младший разряд) – числа  : именно он был отброшен при взятии для : именно он был отброшен при взятии для  целой части частного целой части частного  . Он представляет собой остаток от деления числа . Он представляет собой остаток от деления числа  на на  , то есть в этом случае , то есть в этом случае  . Если происходит сдвиг влево, то получаем . Если происходит сдвиг влево, то получаем  . .
Таким образом, функция 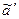 получает следующее описание: получает следующее описание:

В полученных выражениях для функций  задействованы только примитивно рекурсивные функции, и указанные функции получены из этих примитивно рекурсивных функций с помощью оператора условного перехода, который сохраняет свою примитивную рекурсивность, то есть из примитивно рекурсивных функций создает снова примитивно рекурсивную функцию, следовательно, задействованы только примитивно рекурсивные функции, и указанные функции получены из этих примитивно рекурсивных функций с помощью оператора условного перехода, который сохраняет свою примитивную рекурсивность, то есть из примитивно рекурсивных функций создает снова примитивно рекурсивную функцию, следовательно,  – примитивно рекурсивны. – примитивно рекурсивны.
Следовательно, на каждом шаге любая машина Тьюринга осуществляет примитивно рекурсивное вычисление.
IV. Рассмотрим теперь работу машины Тьюринга в целом.
Пусть задана начальная конфигурация  . Так конфигурация K (t), возникающая в момент времени t работы машины Тьюринга, зависит от величины t и . Так конфигурация K (t), возникающая в момент времени t работы машины Тьюринга, зависит от величины t и  , то есть она есть векторная функция , то есть она есть векторная функция 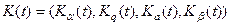 , компоненты которой в свою очередь являются функциями, зависящими от t, , компоненты которой в свою очередь являются функциями, зависящими от t,  . Эти функции определяются следующим образом: . Эти функции определяются следующим образом:


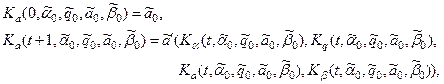

Очевидно, что эти соотношения представляют собой схемы примитивной рекурсии, определяющие функции  с помощью функций с помощью функций  . При этом рекурсия ведется по переменной t. Примитивная рекурсивность функций . При этом рекурсия ведется по переменной t. Примитивная рекурсивность функций  уже установлена, следовательно, функции уже установлена, следовательно, функции 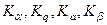 – примитивно рекурсивны. – примитивно рекурсивны.
V. Покажем, что результат работы, т. е. вычисляемая машиной функция, носит рекурсивный характер. Покажем, что всякая функция, правильно вычисляемая на машине Тьюринга, частично рекурсивна. Пусть  – функция, правильно вычислимая машиной Тьюринга. Такая МТ, начав с конфигурации – функция, правильно вычислимая машиной Тьюринга. Такая МТ, начав с конфигурации  , останавливается в конфигурации вида , останавливается в конфигурации вида  , то есть для такой МТ , то есть для такой МТ   , Исходное слово кодируется числом , Исходное слово кодируется числом 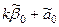 , заключительное слово числом , заключительное слово числом  , то есть вычисляется значение функции , то есть вычисляется значение функции   . Заключительное слово – слово, написанное на ленте в тот момент . Заключительное слово – слово, написанное на ленте в тот момент  , когда МТ перешла в заключительное состояние , когда МТ перешла в заключительное состояние  , т. е. в момент , т. е. в момент  . Поэтому . Поэтому   , ,

Так как  , ,  Ост (x, k), то для Ост (x, k), то для  можно записать: можно записать:
 Ост Ост  Ост Ост 
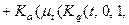 Ост Ост  Ост Ост 
где k, z – константы, зависящие от конкретной машины Тьюринга.
Таким образом, функция  , представляющая собой результат работы машины Тьюринга, построена из простых рекурсивных функций с помощью операции минимизации , представляющая собой результат работы машины Тьюринга, построена из простых рекурсивных функций с помощью операции минимизации  и, следовательно, является частично-рекурсивной. Следовательно, любая вычислимая по Тьюрингу функция частично рекурсивна ¡. и, следовательно, является частично-рекурсивной. Следовательно, любая вычислимая по Тьюрингу функция частично рекурсивна ¡.
Теорема 7.9. Функция вычислима по Тьюрингу тогда и только тогда, когда она частично рекурсивна ¡.
Таким образом, удалось показать, что класс функций, вычислимых по Тьюрингу, совпадает с классом частично рекурсивных функций. Совпадение этих двух классов вычислимых функций, в основе построения которых лежат совершенно разные подходы к формализации понятия вычислимости функции, говорит о том, что эти подходы оказались весьма состоятельными, и служат косвенным подтверждением того, что как тезис Тьюринга, так и тезис Черча имеют право на признание.
|



 местному предикату
местному предикату 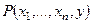 и дающую в результате функцию
и дающую в результате функцию  . Значение
. Значение  на наборе
на наборе  равно наименьшему из таких чисел
равно наименьшему из таких чисел  , что высказывание
, что высказывание  истинно. Если же наименьшего среди таких чисел не существует, то значение функции
истинно. Если же наименьшего среди таких чисел не существует, то значение функции 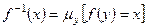 – наименьший
– наименьший  , что
, что  является обратной для функции
является обратной для функции  .
. ,
, . Полагаем
. Полагаем  и, придавая переменной
и, придавая переменной  последовательно значения 0,1,2,…, будем вычислять значение суммы
последовательно значения 0,1,2,…, будем вычислять значение суммы  . Как только она станет равной 7, то соответствующее значение
. Как только она станет равной 7, то соответствующее значение  ,
, ,
,



 :
: ,
, ,
, , …
, …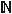
 .
. .
. правильно вычислима по Тьюрингу, то функция
правильно вычислима по Тьюрингу, то функция  , получающаяся с помощью операции минимизации из
, получающаяся с помощью операции минимизации из  машина Тьюринга, правильно вычисляющая
машина Тьюринга, правильно вычисляющая  вычисляет последовательно значения
вычисляет последовательно значения 
 ,
,  до тех пор, пока не получится
до тех пор, пока не получится  . После этого машина Тьюринга должна оставить на ленте число
. После этого машина Тьюринга должна оставить на ленте число  , где
, где  . Если для любого
. Если для любого  , то МТ не должна останавливаться никогда (это означает, что функция g не определена в точке
, то МТ не должна останавливаться никогда (это означает, что функция g не определена в точке  ).
). и
и  .
.
 полагаем, что
полагаем, что 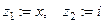 . При выполнении
. При выполнении  -го шага вычисляется
-го шага вычисляется  и проверяется условие
и проверяется условие 
 Выполнение шагов
Выполнение шагов 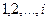 происходит до тех пор, пока не получено равенство
происходит до тех пор, пока не получено равенство  . Иначе
. Иначе  инициализация цикла, запись на ленту блоков
инициализация цикла, запись на ленту блоков 
 .
. вычисление значения
вычисление значения 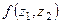 .
. реализация разветвления по условию
реализация разветвления по условию  .
. вычисление
вычисление  .
. стирает блок
стирает блок  .
.

 вычислимы по Тьюрингу, а частично рекурсивная функция получается из простейших с помощью применения конечного числа раз указанных операций, т. е. всякая частично рекурсивная функция вычислима по Тьюрингу ¡.
вычислимы по Тьюрингу, а частично рекурсивная функция получается из простейших с помощью применения конечного числа раз указанных операций, т. е. всякая частично рекурсивная функция вычислима по Тьюрингу ¡. вычислимая по Тьюрингу функция. Тогда существуют машины Тьюринга, осуществляющая для заданного слова
вычислимая по Тьюрингу функция. Тогда существуют машины Тьюринга, осуществляющая для заданного слова  . Разобьем доказательство на этапы.
. Разобьем доказательство на этапы. , где
, где  слово в алфавите
слово в алфавите  записанное на ленте левее обозреваемой в данный момент ячейки;
записанное на ленте левее обозреваемой в данный момент ячейки;  состояние, в котором находится в данный момент машина Тьюринга;
состояние, в котором находится в данный момент машина Тьюринга;  символ в обозреваемой ячейке;
символ в обозреваемой ячейке; 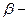 слово в алфавите
слово в алфавите  , записанное на ленте правее обозреваемой ячейки. Указанной конфигурации однозначно сопоставляется упорядоченная четверка
, записанное на ленте правее обозреваемой ячейки. Указанной конфигурации однозначно сопоставляется упорядоченная четверка  чисел, определяемых следующим образом:
чисел, определяемых следующим образом:  ;
; 
 по правилу: эти символы интерпретируются как
по правилу: эти символы интерпретируются как  -значные цифры;
-значные цифры; 
 , но при этом читается справа налево, то есть крайняя слева ячейка
, но при этом читается справа налево, то есть крайняя слева ячейка  сопоставим 1; сдвигу влево
сопоставим 1; сдвигу влево  – 2; отсутствию сдвига
– 2; отсутствию сдвига  сопоставим 0. Закодируем заключительное состояние
сопоставим 0. Закодируем заключительное состояние  символом
символом  , а алфавит
, а алфавит  – числовым множеством
– числовым множеством  .
.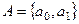 и конфигурация имеет вид
и конфигурация имеет вид (7.6)
(7.6) :
:
 и множеством состояний
и множеством состояний  можно записать:
можно записать:
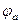 – функция выходов,
– функция выходов,  – функция переходов,
– функция переходов,  – функция движения.
– функция движения. , то
, то 

 , где
, где  , если
, если 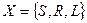 соответственно. Так как
соответственно. Так как  заданы на конечном множестве
заданы на конечном множестве  , то они являются примитивно рекурсивными.
, то они являются примитивно рекурсивными. в новую конфигурацию
в новую конфигурацию  . Это означает, что упорядоченной четверке чисел
. Это означает, что упорядоченной четверке чисел  , однозначно сопоставляется упорядоченная четверка чисел
, однозначно сопоставляется упорядоченная четверка чисел  , соответствующая конфигурация
, соответствующая конфигурация  .
. ранее приведенная конфигурация (7.6) перейдет в конфигурацию
ранее приведенная конфигурация (7.6) перейдет в конфигурацию  , которой соответствует четверка натуральных чисел
, которой соответствует четверка натуральных чисел  .
. , обусловленная данной машиной Тьюринга
, обусловленная данной машиной Тьюринга  . Функция
. Функция  называется функцией следующего шага. Этой функции соответствует четверка числовых функций следующего шага, то есть
называется функцией следующего шага. Этой функции соответствует четверка числовых функций следующего шага, то есть  – числовые функции, каждая из которых зависит от четырех числовых переменных
– числовые функции, каждая из которых зависит от четырех числовых переменных  . Очевидно, что
. Очевидно, что 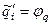 и
и  не зависит от
не зависит от  , а зависит от
, а зависит от  :
: 
 .
. . Если в рассматриваемый момент времени головка машины Тьюринга осталась на месте, то есть обозреваемая ячейка не изменилась и
. Если в рассматриваемый момент времени головка машины Тьюринга осталась на месте, то есть обозреваемая ячейка не изменилась и  , то
, то  . Если головка сдвинулась вправо, то есть
. Если головка сдвинулась вправо, то есть  , то степень каждого разряда числа
, то степень каждого разряда числа  повысилась на единицу: нулевой разряд стал первым, первый – вторым и т.д., то есть число
повысилась на единицу: нулевой разряд стал первым, первый – вторым и т.д., то есть число  число элементов в алфавите
число элементов в алфавите  , а в младший (нулевой) разряд помещается та
, а в младший (нулевой) разряд помещается та  . В итоге получим, что при сдвиге вправо
. В итоге получим, что при сдвиге вправо 
 .
. , степень каждого разряда числа
, степень каждого разряда числа  . Так как младший (нулевой) разряд оказался как бы «обрубленный», то получилась не частное
. Так как младший (нулевой) разряд оказался как бы «обрубленный», то получилась не частное  . Таким образом, для функции
. Таким образом, для функции  получено следующее описание:
получено следующее описание:
 . При сдвиге вправо (влево) она ведет себя также как функция
. При сдвиге вправо (влево) она ведет себя также как функция 
 . Если сдвига не происходит, то
. Если сдвига не происходит, то  . Если происходит сдвиг вправо, то машина Тьюринга переходит к обозрению самого левого разряда (это младший разряд) – числа
. Если происходит сдвиг вправо, то машина Тьюринга переходит к обозрению самого левого разряда (это младший разряд) – числа  : именно он был отброшен при взятии для
: именно он был отброшен при взятии для  . Он представляет собой остаток от деления числа
. Он представляет собой остаток от деления числа  . Если происходит сдвиг влево, то получаем
. Если происходит сдвиг влево, то получаем  .
.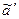 получает следующее описание:
получает следующее описание:
 задействованы только примитивно рекурсивные функции, и указанные функции получены из этих примитивно рекурсивных функций с помощью оператора условного перехода, который сохраняет свою примитивную рекурсивность, то есть из примитивно рекурсивных функций создает снова примитивно рекурсивную функцию, следовательно,
задействованы только примитивно рекурсивные функции, и указанные функции получены из этих примитивно рекурсивных функций с помощью оператора условного перехода, который сохраняет свою примитивную рекурсивность, то есть из примитивно рекурсивных функций создает снова примитивно рекурсивную функцию, следовательно,  . Так конфигурация K (t), возникающая в момент времени t работы машины Тьюринга, зависит от величины t и
. Так конфигурация K (t), возникающая в момент времени t работы машины Тьюринга, зависит от величины t и  , то есть она есть векторная функция
, то есть она есть векторная функция 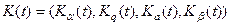 , компоненты которой в свою очередь являются функциями, зависящими от t,
, компоненты которой в свою очередь являются функциями, зависящими от t, 

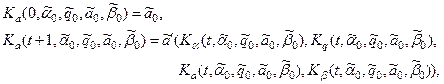

 с помощью функций
с помощью функций 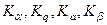 – примитивно рекурсивны.
– примитивно рекурсивны. – функция, правильно вычислимая машиной Тьюринга. Такая МТ, начав с конфигурации
– функция, правильно вычислимая машиной Тьюринга. Такая МТ, начав с конфигурации  , останавливается в конфигурации вида
, останавливается в конфигурации вида  , то есть для такой МТ
, то есть для такой МТ 
 , Исходное слово кодируется числом
, Исходное слово кодируется числом 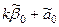 , заключительное слово числом
, заключительное слово числом  , то есть вычисляется значение функции
, то есть вычисляется значение функции 
 . Заключительное слово – слово, написанное на ленте в тот момент
. Заключительное слово – слово, написанное на ленте в тот момент  , когда МТ перешла в заключительное состояние
, когда МТ перешла в заключительное состояние  , т. е. в момент
, т. е. в момент  . Поэтому
. Поэтому 
 ,
,
 ,
,  Ост (x, k), то для
Ост (x, k), то для  можно записать:
можно записать: Ост
Ост  Ост
Ост 
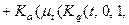 Ост
Ост 
 и, следовательно, является частично-рекурсивной. Следовательно, любая вычислимая по Тьюрингу функция частично рекурсивна ¡.
и, следовательно, является частично-рекурсивной. Следовательно, любая вычислимая по Тьюрингу функция частично рекурсивна ¡.


