
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычислимость по Тьюрингу примитивно рекурсивных функцийСодержание книги
Поиск на нашем сайте
Теорема 7.5. Функция f, полученная при помощи схемы примитивной рекурсии из правильно вычислимых по Тьюрингу функций g и h, является правильно вычислимой по Тьюрингу. Доказательство. Не теряя общности, проведем доказательство для простейшей схемы примитивной рекурсии:
Для схемы (7.1) общего вида операция примитивной рекурсии реализуется аналогично. Опишем выполнение операции в виде композиции машины Тьюринга, осуществляющих циклические вычисления значения
Очевидно, что реализуемы следующие машины Тьюринга:
Совместная работа этих МТ осуществляется согласно схеме, представленной на рис. 7.2 ¡. Следствие. Всякая примитивно – рекурсивная функция вычислима по Тьюрингу.
Функции Аккермана Учитывая тезис Тьюринга, под алгоритмом будем понимать машины Тьюринга. После того, как было доказано, что всякая примитивно рекурсивная функция вычислима по Тьюрингу, возникает вопрос: исчерпывается ли класс вычислимых по Тьюрингу функций примитивно рекурсивными функциями, то есть всякое ли вычислимое по Тьюрингу функция будет примитивно рекурсивна?
Теорема 7.6. Существует функции, не являющиеся примитивно рекурсивными. Доказательство. Очевидно, что множество всех примитивно рекурсивных функций счётно. Это объясняется тем, что каждая примитивно рекурсивная функция имеет конечное описание, то есть задается конечным словом в некотором фиксированном для всех функций алфавите. Множество всех конечных слов счётно, следовательно, примитивно рекурсивных функций не более, чем счетное множество. В тоже время, множество всех функций, даже от одного аргумента из
Существуют функции, являющиеся вычислимыми, но не являющиеся примитивно рекурсивными. Для доказательства этого достаточно построить функцию, которая будет вычислимой, но будет обладать свойством, которым не обладает ни одна примитивно рекурсивная функция. Таким свойством может служить скорость роста функции. То есть укажем вычислимую функцию, которая растет быстрее любой примитивно рекурсивные функции и поэтому примитивной рекурсией не является. Известно, что произведение растет быстрее суммы, а степень – быстрее произведения. Запишем эти функции:
Эти функции связаны между собой рекурсивными соотношениями:
Продолжим эту последовательность, положим по определению для
Первое из равенств (7.4) предназначено для того, что функции
Значение Зафиксируем значение
Функция На основании введенных обозначений и соотношений (7.4) для
Схема (7.5) похожа на схему примитивной рекурсии, но примитивная рекурсия ведется по одному аргументу, а в схеме (7.5) – сразу по двум переменным (такая рекурсия называется двойной или рекурсией второй степени). При этом усложняется характер упорядочения точек, а следовательно, и понятие предшествующей точки. Это упорядочение не определено заранее, так как в схеме примитивной рекурсии, где число Рассмотри свойства функции
Введем понятие
Можно показать, что все примитивно рекурсивные функции Рассмотрим теперь произвольно примитивно рекурсивную функцию Таким образом, показано, что примитивно рекурсивные функции не исчерпывают класса всех вычислимых функций и свойство функции быть примитивно рекурсивной не равносильно ее свойству быть вычислимой (в том числе по Тьюрингу).
|
||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 770; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.165.149 (0.009 с.) |

 (7.3)
(7.3) , а именно: необходимо вычислить
, а именно: необходимо вычислить  значение
значение  . На каждом шаге описываемого цикла на ленте машины Тьюринга будем записывать три блока
. На каждом шаге описываемого цикла на ленте машины Тьюринга будем записывать три блока 

 где
где  . Согласно (7.3) имеем
. Согласно (7.3) имеем 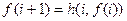 , поэтому при завершении каждого шага цикла производится следующая проверка. Если
, поэтому при завершении каждого шага цикла производится следующая проверка. Если  , то есть
, то есть  , то
, то 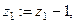
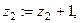
 . Если
. Если  , то есть
, то есть  , то блоки
, то блоки  и
и  затираются и на ленте остаётся
затираются и на ленте остаётся  . В начале на работы на ленте записано:
. В начале на работы на ленте записано:
 инициализация цикла, занесение на ленту значений
инициализация цикла, занесение на ленту значений  ;
; реализует
реализует  реализует
реализует  вычисление
вычисление  , где
, где 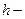 примитивная рекурсивная функция;
примитивная рекурсивная функция; реализует разветвление по условию
реализует разветвление по условию  стирает блоки
стирает блоки  после завершения цикла.
после завершения цикла.
 в
в 
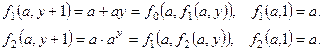
 :
: (7.4)
(7.4) были всюду определены. Схема (7.4) имеет вид примитивной рекурсии и, следовательно, все функции
были всюду определены. Схема (7.4) имеет вид примитивной рекурсии и, следовательно, все функции  примитивно рекурсивны. Растут они крайне быстро. Так,
примитивно рекурсивны. Растут они крайне быстро. Так,
 получается в результате возведения числа
получается в результате возведения числа  в степень
в степень  раз.
раз. . Получим последовательность функций от одного аргумента:
. Получим последовательность функций от одного аргумента: 
 ,… Рассмотрим функции:
,… Рассмотрим функции: ,
,  .
. перечисляет последовательность
перечисляет последовательность 
 ,… Функция
,… Функция 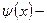 диагональной функцией Аккермана.
диагональной функцией Аккермана.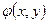 справедливо:
справедливо: (7.5)
(7.5) всегда предшествует числу
всегда предшествует числу 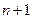 , а выясняется в ходе вычислений и для каждой схемы (7.5), вообще говоря, различно. Так,
, а выясняется в ходе вычислений и для каждой схемы (7.5), вообще говоря, различно. Так,  , а так как
, а так как 
 , то вычислению
, то вычислению  по схеме (7.5) должно предшествовать вычисление значения
по схеме (7.5) должно предшествовать вычисление значения  :
: 
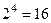 . Аналогично, вычислению значения
. Аналогично, вычислению значения 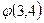 должно предшествовать вычисление значения
должно предшествовать вычисление значения  и так далее. Таким образом,
и так далее. Таким образом,  и
и  вычислимы по схеме (7.5), следовательно, вычислимы по Тьюрингу. Покажем, что
вычислимы по схеме (7.5), следовательно, вычислимы по Тьюрингу. Покажем, что 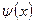 не является примитивно рекурсивными.
не является примитивно рекурсивными.

 мажорируемой функции. Функция
мажорируемой функции. Функция  называется
называется 

 . Затем доказывается, что операция суперпозиции применимая к
. Затем доказывается, что операция суперпозиции применимая к  . Для некоторого
. Для некоторого  и любого
и любого 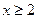 имеем
имеем  . Но тогда
. Но тогда 
 , следовательно,
, следовательно,  начиная с
начиная с  . Получили, что функция
. Получили, что функция 


