
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проблемы распознавания самоприменимости и применимостиСодержание книги
Поиск на нашем сайте
Проблема самоприменимости МТ состоит в следующем. Пусть на ленту МТ Т записан ее собственный шифр Ш(Т). МТ Т начинает работу с крайнего левого непустого символа, находясь в состоянии
Теорема 8.2. Проблема распознавания самоприменимых машин Тьюринга алгоритмически неразрешима. Доказательство. От обратного: предположим, что проблема самоприменимости алгоритмически разрешима, т.е. существует МТ
где Если МТ Сама машина Таким образом, предположение существования МТ Метод алгоритмической сводимости Рассмотрим метод алгоритмической сводимости, который позволяет доказывать неразрешимость некоторой проблемы, если к ней сводится другая проблема, неразрешимость которой уже доказана. Пусть
Теорема 8.3. Если проблема Доказательство. Если бы проблема
Отношение сводимости обладает свойством транзитивности: если Будем считать, что применяется метод алгоритмической сводимости если, используя теорему 8.3 и неразрешимую проблему Рассмотрим проблему останова МТ. Нужно по заданной МТ Т и слову на ленте выяснить, применима ли МТ Т к слову
Теорема 8.4. Проблема останова неразрешима. Доказательство. Покажем, что неразрешимая проблема самоприменимости сводится к проблеме останова. Действительно, алгоритм преобразования состоит в переписи Шифра МТ Т в качестве исходного слова Примеры алгоритмически неразрешимых проблем Рассмотрим еще несколько проблем, которые являются алгоритмически неразрешимыми. 1. Проблема выводимости в Марковской системе подстановок из заданного слова Теорема 8.5. Существует система нормальных подстановок и слово
2. Неразрешимой является проблема эквивалентности алгоритмов: по двум данным алгоритмам нельзя узнать, вычисляют они одну и ту же функцию или нет. Каждый кто сталкивается с написанием компьютерных программ, знает, что по тексту программы, не запуская ее в работу, трудно понять, что она делает (какую функцию вычисляет). 3. Не существует алгоритма, позволяющего для каждой формулы логики предикатов определить, будет ли эта формула выполнима или общезначима. 4. 10-ая проблема Гильберта (поставлена в 1901 г. на международном математическом конгрессе в Париже): Требуется найти алгоритм, определяющий для любого диафантова уравнения вида f (x, y,…, z)=0, где f (x, y,…, z) – многочлен с целыми показателями степеней и целыми коэффициентами, имеет ли оно целочисленное решение. В общем случае эта проблема долго оставалась не решенной, и только в 1970 г. советский математик Ю.В. Матиясевич доказал ее неразрешимость.
Итак, отметим, что алгоритмическая неразрешимость означает лишь отсутствие единого способа для решения всех единичных задач данной массовой проблемы, в то время как каждая индивидуальная задача проблемы вполне может быть решена своим индивидуальным способом. Более того, может оказаться разрешимой своим индивидуальным способом не только каждая отдельная задача этого класса, но и целые подклассы задач данного класса. Поэтому, если проблема неразрешима в общем случае, нужно искать ее разрешимые частные случаи.
[1] ТЬЮРИНГ, Алан Матисон (Turing) (1912–1954) – английский математик, логик, криптограф. Окончил Кембриджский ун-т (1935). В 1936 г., используя схему абстрактной машины, доказал ряд важных положений в области мат.логики. В годы Второй мировой войны возглавил работу по созданию вычислительных машин в Нац. физической лаборатории. Его работы по сооружению первых ЭВМ и развитию методов программирования дали основу исследований в области искусственного интеллекта.
[2] АККЕРМАН, Вильгельм (Ackermann) (1896–1962) – Немецкий математик и логик, ученик Д. Гильберта. Родился в Шёнебек. Был профессором в Мюнстере. Основные труды относятся к математической логике. Книга «Основы теоретической логики», написанная совместно с Д. Гильбертом, переведена на русский язык в 1947. [3] МАРКОВ, Андрей Андреевич (1903–1979) – советский математик, чл.-корр АН СССР. Окончил Ленинградский гос. университет (1924). Основные труды по теории динамических систем, топологии, топологической алгебре, теории алгоритмов и конструктивной математике. Доказал неразрешимость проблемы равенства в ассоциативных системах (1947), проблемы гомеоморфии в топологии (1958), создал школу конструктивной математики и логики в СССР, автор понятия нормального алгорифма.
|
||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 721; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.125.240 (0.01 с.) |

 . Если, начав вычисление в указанной конфигурации, МТ Т остановится за конечное число шагов, то она называется самоприменимой, иначе несамоприменимой. Проблема самоприменимости состоит в установлении для произвольной МТ Т свойства: является ли Т самоприменимой или нет.
. Если, начав вычисление в указанной конфигурации, МТ Т остановится за конечное число шагов, то она называется самоприменимой, иначе несамоприменимой. Проблема самоприменимости состоит в установлении для произвольной МТ Т свойства: является ли Т самоприменимой или нет. , которая для произвольной МТ Т переводит конфигурацию
, которая для произвольной МТ Т переводит конфигурацию  в конфигурацию
в конфигурацию  , если МТ Т самоприменима, и в
, если МТ Т самоприменима, и в 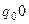 если МТ Т несамоприменима. Здесь
если МТ Т несамоприменима. Здесь  – заключительное состояние МТ
– заключительное состояние МТ  , добавив две новые команды
, добавив две новые команды (
( )
)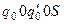 , (
, ( )
) – заключительное состояние МТ
– заключительное состояние МТ  , являющегося шифром самоприменимой МТ Т, то она, согласно командам МТ
, являющегося шифром самоприменимой МТ Т, то она, согласно командам МТ  и «зациклится» в силу команды (
и «зациклится» в силу команды ( ). Получили, что МТ
). Получили, что МТ 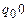 и по команде (
и по команде ( ), остановится в состоянии
), остановится в состоянии  применима к шифру несамоприменимых машин.
применима к шифру несамоприменимых машин. и
и  – две проблемы. Пусть существует МТ Т, которая позволяет преобразовывать любую задачу
– две проблемы. Пусть существует МТ Т, которая позволяет преобразовывать любую задачу  в задачу
в задачу  , т.е.
, т.е.  , таким образом, что задача
, таким образом, что задача  дает ответ «да» тогда и только тогда, когда задача
дает ответ «да» тогда и только тогда, когда задача  дает ответ «да». В случае, когда такое преобразование имеет место, то считается, что проблема
дает ответ «да». В случае, когда такое преобразование имеет место, то считается, что проблема  алгоритмически сводится к проблеме
алгоритмически сводится к проблеме  .
. также является неразрешимой.
также является неразрешимой.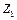 сводится к
сводится к  , а
, а 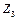 , то
, то  сводится к
сводится к  .
. или нет, т.е. остановится ли она за конечное число шагов, начав работу в конфигурации
или нет, т.е. остановится ли она за конечное число шагов, начав работу в конфигурации  .
. . МТ Т начинает работу с конфигурации
. МТ Т начинает работу с конфигурации 
 . МТ
. МТ  применима к слову
применима к слову 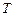 – самоприменима. В силу построенного сведения, проблема останова неразрешима ¡.
– самоприменима. В силу построенного сведения, проблема останова неразрешима ¡. выяснить, выводимо ли оно из слова
выяснить, выводимо ли оно из слова 


