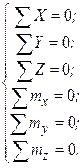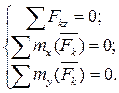Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Если система сил имеет равнодействующую, то момент равнодействующей относительно любого центра равен сумме моментов составляющих относительно того же центра.Содержание книги
Поиск на нашем сайте
но Теорема о параллельном переносе силы Силу можно переносить параллельно самой себе из данной точки в любую другую, добавляя при этом, пару сил с моментом, равным моменту переносимой силы относительно новой точки приложения.
Основная теорема статики Определение: главным вектором системы сил называется вектор, равный геометрической сумме сил системы: Определение: главным моментом системы относительно центра О называется вектор, равный геометрической сумме моментов всех сил системы относительно этого центра. Статика решает две главные задачи: 1. Задачу о равновесии (каким условиям должна удовлетворять система сил, для того чтобы тело под ее действием находилось в равновесии); 2. Задачу о приведении (как данную систему сил заменить другой, в частности более простой). Вторую задачу статики помогает решить основная теорема статики: любую систему сил можно заменить одной силой, равной главному вектору и приложенной в центре приведения, и одной парой сил с моментом, равным главному моменту относительно центра приведения. Доказательство: пусть на тело (рис. 19) действует система сил
Случаи приведения
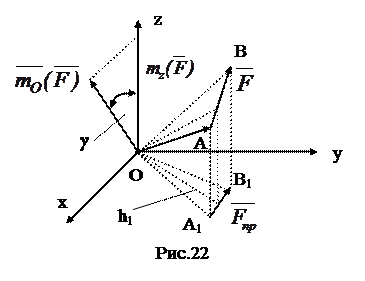
2. 3. 4. а) h = | б) Во всех остальных случаях система может быть приведена к динаме. Под действием динамы тело может совершать винтовое движение. Момент силы относительно оси Моментом силы относительно оси называется алгебраическая величина, равная проекции момента силы относительно точки, лежащей на оси, на эту ось (рис.22). Таким образом, Векторное произведение двух векторов можно представить в виде определителя. Разложив его по элементам первой строки, получим:
С другой стороны,
При решении задач удобно определять момент силы относительно оси по следующему правилу: момент силы относительно оси равен моменту проекции силы на плоскость, перпендикулярную оси относительно точки пересечения оси и плоскости, т.е.: m Вывод: момент силы относительно оси равен нулю, если сила параллельна оси (Fпр=0) или сила пересекает ось (h Геометрически момент силы относительно центра О равен удвоенной площади Δ ОАВ, а относительно оси z - удвоенной площади Δ ОА1В1. Уравнения равновесия произвольной пространственной Системы сил Для равновесия необходимо, чтобы выполнялось два равенства:
Поскольку |
Если линии действия всех сил системы параллельны, то, выбрав ось z параллельной линиям действия сил, получим, что первые два и последнее уравнение системы выполнятся тождественно. Тогда останутся три уравнения равновесия:
|
||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 317; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.95.120 (0.009 с.) |

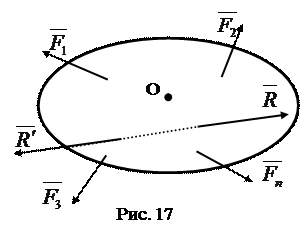 Пусть (рис. 17) система
Пусть (рис. 17) система  имеет равнодействующую
имеет равнодействующую 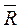 . Приложим к телу силу
. Приложим к телу силу 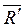 = -
= - 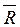 , тогда система
, тогда система 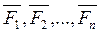 ,
, 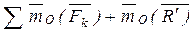 =0.
=0.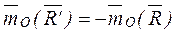 , тогда
, тогда 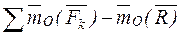 = 0. следовательно,
= 0. следовательно, 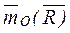 =
= 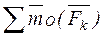 . Что и требовалось доказать.
. Что и требовалось доказать.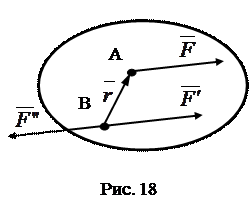 Доказательство (рис.18): пусть в точке А приложена сила
Доказательство (рис.18): пусть в точке А приложена сила  . Приложим в точке В силы
. Приложим в точке В силы  и
и  , равные, параллельные силе
, равные, параллельные силе 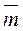 (
(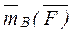 =
= 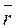 ×
×  .
.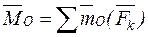 .
.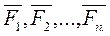 . Выберем произвольно т. О – центр приведения. По теореме о параллельном переносе, каждую из сил можно перенести в центр О, добавив при этом соответствующую пару сил. В результате, перенеся все силы в точку О, получим систему сил, приложенных в т. О, и систему пар сил с моментами равными моментам сил системы относительно центра О. Сложив все силы, приложенные к центру О, получим главный вектор системы
. Выберем произвольно т. О – центр приведения. По теореме о параллельном переносе, каждую из сил можно перенести в центр О, добавив при этом соответствующую пару сил. В результате, перенеся все силы в точку О, получим систему сил, приложенных в т. О, и систему пар сил с моментами равными моментам сил системы относительно центра О. Сложив все силы, приложенные к центру О, получим главный вектор системы 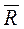 . Сложив все моменты пар сил, получим главный момент
. Сложив все моменты пар сил, получим главный момент  . Таким образом, данную систему сил заменили одной силой
. Таким образом, данную систему сил заменили одной силой 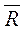 и одной парой сил с моментом
и одной парой сил с моментом 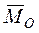 , что и требовалось доказать.
, что и требовалось доказать.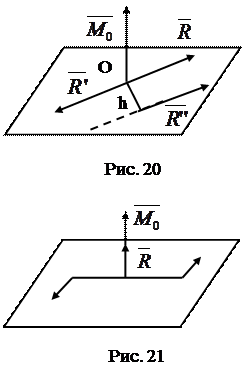 1.
1.  = 0,
= 0,  = 0. Система сил эквивалентна нулю, т.е. находится в равновесии.
= 0. Система сил эквивалентна нулю, т.е. находится в равновесии. 0. Система приводится к паре сил. При этом главный момент не зависит от выбора центра приведения.
0. Система приводится к паре сил. При этом главный момент не зависит от выбора центра приведения. . Система приводится к равнодействующей, лежащей на расстоянии
. Система приводится к равнодействующей, лежащей на расстоянии | / |
| / | 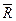 | от центра приведения (рис. 20).
| от центра приведения (рис. 20).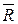 ||
|| 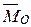 . В этом случае система приводится к динаме, или силовому винту (рис.21).
. В этом случае система приводится к динаме, или силовому винту (рис.21).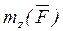 = |
= |  | cosγ.
| cosγ.
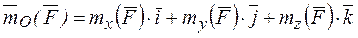 .
. Сравнивая эти формулы, получаем:
Сравнивая эти формулы, получаем: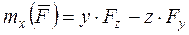 ;
; 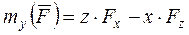 ;
; 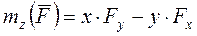 .
.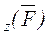 = mO
= mO  =
= 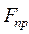 ·h
·h 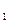 .
.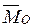 = 0.
= 0.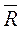 |
|  , а |
, а | 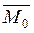 | =
| = 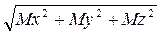 , то для выполнения этих равенств необходимо, чтобы одновременно выполнялись шесть уравнений:
, то для выполнения этих равенств необходимо, чтобы одновременно выполнялись шесть уравнений:
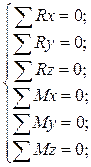 или
или  или
или