
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные положения гидродинамикиСодержание книги
Поиск на нашем сайте
ГАЗОВОГО ПОТОКА Промышленные газы и воздух, содержащие взвешенные твердые или жидкие частицы, представляют собой двухфазные системы, состоящие из непрерывной (сплошной) среды и дисперсной фазы. Сплошной фазой в данном случае являются газы, дисперсной - твердые частицы или капельки жидкости. Подобные двухфазные системы получили название аэродисперсных систем или аэрозолей. Вопросы гидродинамики газового потока изложены в целом ряде фундаментальных монографий, поэтому ограничимся лишь самыми основными положениями, необходимыми для последующего изложения [2]. Теория движения газового потока базируется на двух основных уравнениях гидродинамики: уравнении неразрывности движения и динамическом уравнении движения несжимаемой жидкости (уравнении Навье - Стокса). Уравнение неразрывности (сплошности) потока:
где ρ- плотность среды (газов), кг/м3; τ- продолжительность, с; υ- скорость газа (среды), м/с; х, у, z-направление осей координат. Представляет собой выражение закона сохранения энергии, согласно которому изменение массы определенного элементарного объема газов компенсируется соответствующим изменением его плотности ( Второе основное уравнение гидродинамики, уравнение Навье- Стокса, определяет систему сил, действующих в жидкости (газе), и по направлениям осей координат для элементарного объема жидкости (рис. 1) может быть представлено в виде:
(1.2) где Анализ уравнения (1.2) показывает, что оно учитывает действие четырех сил: тяжести, давления, внутреннего трения (вязкости) и инерции. Сила тяжести (ρg) представляет собой внешний фактор, а остальные силы - результат действия окружающей среды на выделенный элементарный объем. Дифференциальные уравнения (1.1) и (1.2) характеризуют внутренний механизм процесса, устанавливают взаимосвязь между физическими условиями процесса и изменениями этих условий во времени. Однако дифференциальные уравнения не учитывают внешних воздействий на систему, и поэтому должны быть дополнены граничными условиями, характеризующими взаимодействие системы с внешней средой.
Рисунок1.1 - К выводу уравнения Навье-Стокса. При обтекании газами твердых тел в непосредственной близости к их поверхности образуется неподвижный слой. Хотя толщина этого слоя очень мала (всего несколько молекулярных слоев), он оказывает существенное влияние на течение. Принято считать, что граничным условием при обтекании движущейся средой всех твердых поверхностей является равенство υгп = 0 (где υгп- скорость газов на поверхности тела). На границе раздела двух фаз газ - жидкость скорость не должна установиться равной нулю, но выполняются следующие граничные условия: 1) тангенциальная слагающая скорости υт непрерывна, υгт= υжт(индексы «г» и «ж» относятся к газу и жидкости); 2) нормальная слагающая скорости равна нулю: υгн = υжт = 0. 3) силы, с которыми жидкость и газы действуют друг на друга, равны и противоположны по направлению. Наряду с граничными условиями для характеристики состояния системы в начальный момент процесса приводятся начальные условия. Граничные и начальные условия в совокупности представляют собой краевые условия, выделяющие пространственно-временную область, в которой рассматривается процесс, и обеспечивающие единственность решения задачи. Уравнения (1.1) и (1.2) фактически образуют систему с двумя неизвестными υги ρ. Решить подобную систему в общем виде весьма трудно. Приближенное решение удается получить только в отдельных случаях, когда идут по пути упрощений уравнений с учетом конкретно поставленной задачи. Многие важные результаты при решении практических задач гидродинамики были получены благодаря применению методов теории подобия [3]. В результате подобного преобразования дифференциальные уравнения движения тазового потока могут быть заменены критериальным уравнением
где
Вид функциональной связи между критериями в уравнении (1.3) устанавливается опытным путем, причем критерий Важнейшей характеристикой процесса движения газового потока является критерий Турбулентное течение жидкости. Автомодельный режим. Истинное значение любой величины для конкретного момента движения в данной точке при турбулентном режиме представляет собой сумму величин, характеризующих основное и пульсационное течения. Турбулентные пульсации определяются как их скоростью, так и масштабом движения. Самые быстрые пульсации имеют наибольший масштаб. Так, при движении в трубе масштаб наибольших пульсаций совпадает с диаметром трубы. Величина пульсаций оценивается критерием Мелкомасштабные пульсации возникают в результате наложений крупномасштабных пульсаций. При некотором значении λ = λ0 Турбулентный поток может быть охарактеризован некоторой константой εп, выражающей величину потери энергии(в Дж за 1 с в единице объема)
Многие важные зависимости, применяемые в механике аэрозолей и связанные с турбулентным движением газового потока, содержат величину отношения Скорость мелкомасштабных пульсаций (λ<<
Уменьшению скорости и масштаба пульсаций соответствует уменьшение числа Reλ по закону
Откуда масштабλ0, при котором
Начиная с λ = λ0движение газов принимает вязкий характер, и турбулентные пульсации масштаба λ≤λ0постепенно затухают. При движении газового потока вдоль стенки на расстоянии zот нее средняя скорость потока может быть найдена по формуле, предложенной Прандтлем:
где υz-средняя скорость потока на расстоянии zот стенки, м/с; υ* -характерная для данного потока скорость турбулентных пульсаций, м/с. В гладких трубах при
На весьма малом расстоянии от стенки, где имеется вязкий подслой (пограничный слой) толщиной δ0 эта формула неприменима. Движение газового потока в пылеуловителях обычно протекает при больших значениях критерия ζ = где ζ- коэффициент гидравлического сопротивления; А, С увеличением влияния инерционных сил [3] происходит уменьшение показателя степени у критерия Вследствие трения в газовом потоке вокруг обтекаемого тела или у стенки, вдоль которой он движется, образуется пограничный слой. За толщину пограничного слоя δ0 принимается толщина слоя газов, в котором происходит изменение скорости движения от 0 до характерной для потока величины υг. Исключительно важную роль играет пограничный слой при турбулентном движении. Однако до настоящего времени нет единого подхода к оценке характера движения в нем. Распределение скоростей в турбулентном пограничном слое может быть определено из выражения
а сама толщина слоя - из выражения
В пограничном слое движение газового потока строго ламинарно. Ввиду отсутствия турбулентных пульсаций перенос вещества осуществляется в нем преимущественно за счет молекулярной диффузии. В пограничном слое турбулентные пульсации не исчезают внезапно, а постепенно затухают, приближаясь к поверхности стенки (или обтекаемого тела). При z<δ0 поток вещества, переносимый турбулентными пульсациями, меньше, чем поток, переносимый за счет молекулярной диффузии. Тем не менее наличие турбулентных пульсаций в пограничном слое играет важную роль при переносе вещества к твердой поверхности. В диффузионном подслое толщиной δд (δ0>>δд), который находится у стенки, молекулярная диффузия полностью преобладает над турбулентной. На границе диффузионного подслоя совпадают коэффициенты турбулентной и молекулярной диффузии. Величина диффузионного подслоя может быть найдена из выражения
где При обтекании тел, имеющих значительную кривизну (сфера, цилиндр и т. п.), картина образования пограничного слоя имеет довольно сложный характер. Так, в случае обтекания цилиндра на фронтальной его части образуется пограничный слой, аналогичный слою, образующемуся на плоской стенке. Однако переменные величины скорости и давления газового потока, движущегося вокруг цилиндра (вне пограничного слоя), приводят к отрыву газовых струй от поверхности. Скорость газов минимальная в передней точке (точке набегания), плавно нарастает до экваториальной плоскости, а затем снова уменьшается. Давление же газов изменяется от максимума в точке набегания до минимума в экваториальном сечении с последующим возрастанием в «кормовой части» цилиндра. Поэтому в передней части цилиндра газы в пограничном слое движутся в направлении градиента давления, в задней части - в направлении, противоположном градиенту давления. Градиент давления тормозит медленно движущиеся слои газов в прилегающем к обтекаемому телу слою, и в некоторой точке за экваториальной плоскостью противодавление полностью затормозит газовый поток у поверхности. Ниже этой точки вблизи стенки возникает возвратное движение газов, слои газов из пограничного слоя оттесняются от поверхности тела. Оторвавшийся пограничный слой в виде вихря движется в общем газовом потоке. Отрыв вихрей начинается при значениях критерия Рейнольдса для обтекаемого тела
|
||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 443; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.133.214 (0.013 с.) |


 ). Для обычно рассматриваемого на практике случая установившегося движения
). Для обычно рассматриваемого на практике случая установившегося движения 



 - давление в рассматриваемой точке потока, Па; μ- динамическая вязкость среды (газов), Па·с.
- давление в рассматриваемой точке потока, Па; μ- динамическая вязкость среды (газов), Па·с. (1.3)
(1.3) /
/  - критерий Фруда, характеризующий отношение силы инерции к силе тяжести;
- критерий Фруда, характеризующий отношение силы инерции к силе тяжести;  - определяющий линейный параметр, м;
- определяющий линейный параметр, м;  /
/  критерий Эйлера, характеризующий отношение силы давления к силе инерции (
критерий Эйлера, характеризующий отношение силы давления к силе инерции ( - перепад давления, Па; ρг- плотность газов, кг/м3);
- перепад давления, Па; ρг- плотность газов, кг/м3);  /
/  - критерий Рейнольдса, характеризующий отношение cилы инерции к силе трения μг- динамическая вязкость газов, Па·с).
- критерий Рейнольдса, характеризующий отношение cилы инерции к силе трения μг- динамическая вязкость газов, Па·с). , включающий в себя переменную
, включающий в себя переменную  , не является определяющим и находится в результате решения уравнения (1.3). Критерий
, не является определяющим и находится в результате решения уравнения (1.3). Критерий  играет важную роль, когда на движение потока оказывают существенное влияние гравитационные силы. При решении многих практических задач оказывается, что действие силы тяжести весьма незначительно, и им можно пренебречь. Практически сила тяжести не учитывается и в общем случае вынужденного движения газового потока, т. е. как бы происходит вырождение критерия
играет важную роль, когда на движение потока оказывают существенное влияние гравитационные силы. При решении многих практических задач оказывается, что действие силы тяжести весьма незначительно, и им можно пренебречь. Практически сила тяжести не учитывается и в общем случае вынужденного движения газового потока, т. е. как бы происходит вырождение критерия  . При малых значениях критерия
. При малых значениях критерия  =υλλ/νг (где υλ- скорость пульсаций; λ - масштаб движения; νг- кинематическая вязкость газов, м2/с). У крупномасштабных пульсаций значение величины
=υλλ/νг (где υλ- скорость пульсаций; λ - масштаб движения; νг- кинематическая вязкость газов, м2/с). У крупномасштабных пульсаций значение величины  (при движении по трубе диаметром Dтp фактор λ = Dтp) и вязкие силы не оказывают никакого влияния на движение потока.
(при движении по трубе диаметром Dтp фактор λ = Dтp) и вязкие силы не оказывают никакого влияния на движение потока.
 /ρг, которая обозначается через
/ρг, которая обозначается через 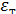 и измеряется в м2/с3.
и измеряется в м2/с3.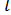 ) в газовом объеме, т. е. вдали от стенок, при невязком характере движения (λ>>λ0) может быть определена из выражения
) в газовом объеме, т. е. вдали от стенок, при невязком характере движения (λ>>λ0) может быть определена из выражения

 =1, будет соответственно равен
=1, будет соответственно равен

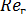 <105 величина υ* может быть найдена из выражения:
<105 величина υ* может быть найдена из выражения: (1.9)
(1.9) (1.10)
(1.10)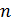 - постоянные.
- постоянные. =0,25; при 105<
=0,25; при 105< 


 =νг/D- критерий Шмидта; D- коэффициент молекулярной (тепловой) диффузии, м2/с.
=νг/D- критерий Шмидта; D- коэффициент молекулярной (тепловой) диффузии, м2/с. = υг
= υг 


