
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гравитационное Осаждение частицСодержание книги
Поиск на нашем сайте
В аппаратах, использующих этот принцип улавливания пыли, осаждение взвешенных частиц происходит под действием силы тяжести. При падении частица пыли испытывает сопротивление среды. Наиболее просто это сопротивление описывается при прямолинейном и равномерном движении шаровой частицы, т. е. в том случае, когда можно пренебречь турбулентностью потока и конвекционными токами. Сила сопротивления, действующая на частицу при ее движении, Fс (H) может быть выражена уравнением:
где ζч- коэффициент лобового сопротивления частицы; sч- площадь сечения частицы, перпендикулярного направлению движения, м2; υч- скорость движения частицы, м/с; ρг- плотность газа, кг/м3. В случае шаровой частицы sч =
Коэффициент ζч зависит от критерия Рейнольдса для частицы ( При обычно соблюдаемом в промышленной практике соотношении
1 - область действия закона Стокса; 2 - стандартная кривая; 3 - область действия формулы Ньютона. Рисунок 2.1 - Зависимость коэффициента лобового сопротивления шаровой частицы от критерия Для частиц размером 0,2-2,0 мкм в уравнение (2.4) вводится поправка Кенингема - Милликена, учитывающая повышение подвижности частиц, размер которых сравним со средней длиной свободного пробега газовых молекул
Поправка
В свою очередь
где Для воздуха при tг=20°С и нормальном атмосферном давлении Ниже приведены значения поправок
Подставляя (2.4) в выражение (2.3), получим для области действия закон Стокса ζч = 24/ Закон Стокса применим при ламинарном движении частиц, когда
Для турбулентного режима движения частиц ( ζч= 18,5/ При значениях ζч = 55/ В более широком диапазоне значений lgζч = 0,113(lg Относительная погрешность при расчетах по формуле (2.11) не превышает 5%. В случае не шарообразных частиц вводится понятие динамического коэффициента формы х, определяемого из выражения
где При определении скорости осаждения частиц не шарообразной формы в расчетных формулах величина ζч заменяется на ζч х, а вместо диаметра Ниже приводятся значения динамического коэффициента формы для частиц
Величина ζч для изометрических частиц в широком интервале значений В общем виде конечная скорость частицы υч (м/с), достигаемая при установлении равенства между силой сопротивления среды и внешней силой Fв (H), действующей на частицу, определяется по формуле
Рисунок2.2 - Зависимость коэффициента сопротивления изометрических частиц от критерия В области действия закона Стокса выражение (2.13) принимает вид:
При гравитационном осаждении шаровой частицы
где Откуда скорость осаждения (в области действия закона Стокса)
Если пренебречь ρг, то величина υcсоставит
где τр- время релаксации частицы, с. Из формулы (2.17) следует, что скорость осаждения взвешенных частиц в газоочистных аппаратах, использующих действие силы тяжести, прямо пропорциональна квадрату диаметра частицы.
Ниже приводятся скорости падения частиц плотностью ρч=1000 кг/м3 в неподвижном воздухе под действием силы тяжести: Диаметр частицы, мкм 100 10 1 Скорость падения, м/с 0,3 0,003 0,00003 Величину υс при гравитационном осаждении частиц в воздухе можно определить с помощью графика, приведенного на рис. 2.3. На графике приведены скорости осаждения при температуре воздуха 15°С в зависимости от диаметра частиц и их плотности, а также скорости осаждения частиц, имеющих плотность ρч = 2000 кг/м3 и оседающих под действием силы, превышающей силу тяжести в 10, 100 и 1000 раз. 1 - под действием силы тяжести; 2 - 4 - под действием силы, превышающей силу тяжести соответственно в 10, 100, 1000 раз Рисунок 2.3 - Диаграмма для определения скорости осаждения частиц в воздухе. На рис. 2.4 приведена зависимость [2] модифицированного коэффициента сопротивления от критерия Рисунок2.4 - Зависимость коэффициента сопротивления сферической частицы, падающей с ускорением ач (м/с2) в воздухе, от критерия Параметр гравитационного осаждения
Уравнение (2.18) может быть представлено также в виде отношения двух критериев G = Stk/Fr (2.19) где С учетом уравнения (2.19) определяется и коэффициент осаждения частиц под действием гравитационных сил в подобных геометрических системах в виде зависимости
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 394; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.212.193 (0.01 с.) |


 /4, где
/4, где  -диаметр частицы (м), и
-диаметр частицы (м), и
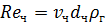 /
/  , где
, где  >>
>>  i(где
i(где 
 .
.
 рассчитывается по уравнению:
рассчитывается по уравнению:
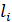 можно рассчитать по уравнению
можно рассчитать по уравнению (2.7)
(2.7) - масса 1 кмоль газов, кг/кмоль;
- масса 1 кмоль газов, кг/кмоль;  -универсальная газовая постоянная;
-универсальная газовая постоянная;  - абсолютная температура газов, К.
- абсолютная температура газов, К. = 6,5·10-8 м.
= 6,5·10-8 м. в соответствии с уравнением (2.6) для воздуха при нормальных условиях:
в соответствии с уравнением (2.6) для воздуха при нормальных условиях: , мкм....……..0,003 0,01 0,03 0,1 0,3 1,0 3,0 10,0
, мкм....……..0,003 0,01 0,03 0,1 0,3 1,0 3,0 10,0 ……………….90,0 24,5 7,9 2,9 1,57 1,16 1,03 1,0
……………….90,0 24,5 7,9 2,9 1,57 1,16 1,03 1,0 ≤2. Причем решающее значение для определения применимости закона Стокса принадлежит в обычных практических условиях размеру частиц.
≤2. Причем решающее значение для определения применимости закона Стокса принадлежит в обычных практических условиях размеру частиц. >500) коэффициент ζч можно принимать постоянным, равным 0,44 (формула Ньютона). Для переходного режима (2<
>500) коэффициент ζч можно принимать постоянным, равным 0,44 (формула Ньютона). Для переходного режима (2< 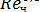 (2.9)
(2.9) (2.10)
(2.10) (2.12)
(2.12) - эквивалентный диаметр частицы, равный диаметру шара, объем которого равен объему данной частицы, м.
- эквивалентный диаметр частицы, равный диаметру шара, объем которого равен объему данной частицы, м. .
.
 с:1 - 670; 2 - 806; 3 - 846; 4 - 245; 5 - 100
с:1 - 670; 2 - 806; 3 - 846; 4 - 245; 5 - 100 (2.14)
(2.14)
 - плотность частицы, кг/м3.
- плотность частицы, кг/м3.

 равен отношению силы тяжести
равен отношению силы тяжести  (Н) и силе сопротивления среды и может быть выражен отношением скорости осаждения частицы к скорости газового потока υг(в м/с):
(Н) и силе сопротивления среды и может быть выражен отношением скорости осаждения частицы к скорости газового потока υг(в м/с):
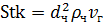 /
/  критерий Стокса; Fr=
критерий Стокса; Fr= 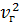 /
/  - критерий Фруда;
- критерий Фруда;  -определяющий линейный параметр, м.
-определяющий линейный параметр, м.



