Закон сохранения момента импульса системы частиц относительно неподвижной (ых) точки и оси

Как отмечалось ранее, наличие системы частиц означает, что силы, действую�щие на каждую частицу системы, можно разделить на внут-

р�енние

F внут

(действующие между частицами системы) и внешние

F внеш (действующие на частицы системы со стороны внешних тел).

 

внешнее тело

 

F внут

21 v

внеш

F 2

r 2 О

l r 1

 

внешнее тело

 

F

 

 

внешнее тело

r 12

v 1

внеш

 

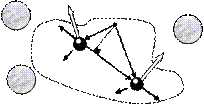
внут

F 12

Рис. 4.6

Рассмотрим на примере простейшей системы, состоящей из двух частиц, свойства внутренних сил и их моментов (рис. 4.6). Выберем

 

произвольную точку О и построим радиус-векторы частиц � и � от-

r 1 r 2

носительно этой точки. По правилу суммирования векторов имеем

= +

� � �

r 1 r 2 r 12.

По третьему закону Ньютона для внутренних сил

� �

12 21

F внут =- F внут,

и эти силы действуют по прямой, соединяющей частицы системы (для определенности взяты силы отталкивания). Тогда сумма внутренних сил и сумма моментов внутренних сил, приложенных к частицам от- носительно произвольной точки О, равны соответственно

� � � �

12 21 12 12

�

�

�

�

F внут + F внут = F внут - F внут =0

 

 

�

внут

 

 

�

внут

� внут

� внут

� � внут

� внут

M 12

+ M 21

= [ r 1, F 12

] + [ r 2, F 21

] = [ (r 2+ r 12), F 12

] – [ r 2, F 12 ] =

� � � � � � � �

= [ r, внут ] + [, внут ] – [, внут ] = [, внут ].

 

Так как

2 F 12

r 12

F 12

 

�

r 2 F 12

�

r 12

F 12

r ­­ F внут,

12 12

и векторное произведение двух параллельных векторов равно нулю, то

� �

12 21

M внут + M внут =0.

Таким образом, обобщая полученные результаты на систему, со- стоящую из произвольного числа частиц, получаем (индексы i и j ну- меруют частицы системы):

F внут =å F внут =0, (4.18)

� �

ij

i >1

M внут =å M внут =0. (4.19)

� �

ij

i >1

Векторная сумма внутренних сил и моментов этих сил системы час-

тиц относител � ьно произвольной точки О равна нулю.

Моментом L импульса системы частиц относительно точки О на-

зывается векторная сумма моментов импульсов всех частиц системы относительно этой точки

å å

� � � �

L = Li = [ ri, pi ], (4.20)

i i

� где Li тицы.

— момент импульса, �

pi

ri

�

— импульс и � — радиус-вектор i час-

Моментом M сил, действующих на систему частиц относитель-

� �

�

�

но точки О, называется векторная сумма моментов сил, действую- щих на все частицы системы относительно этой точки. Так как сум- ма моментов внутренних сил равна нулю (4.19), то

внеш

внеш

� внеш

M = M = å Mi =å[ ri, Fi

], (4.21)

i

� i � i

M

где

внеш

i

— момент внешней силы

F внеш, действующей на i -ю час-

тицу.

�

� �

Рассмотрим, как связаны друг с другом моменты импульса и сил системы, если их брать относительно точек O' и O, находящихся на расстоянии R друг от друга. Для радиус-вектора i частицы системы (рис.4.4) имеем

ri = ri ¢ + R,

�

� � �

где R — радиус- вектор точки O относительно точки O'. Тогда

å[ r, p ] = å[(¢ +

� � � � � �

å å

), ] = [ ¢, ] + [, ] =

 

i i

i � i

ri R pi

� �

ri pi

� i �� i

R pi

= L ¢ + [ R,å pi ] =

i

L ¢ + [ R, p ],

p pi

где � = å�

i

— импульс системы частиц. Подставляя данное равен-

ство в (4.20), получим � � � �

L = L ¢ + [ R, p ].

Аналогично имеем

� � � �

i

M = M ¢ + [ R,å F внеш ]. (4.22)

i

Отметим, что если �

i

å F внеш = 0,

i

то � �

M = M ¢,

т. е. сумма моментов внешних сил, действующих на систему час- тиц, рассчитанных относительно любой неподвижной точки О, оди- накова.

 

На примере простейшей системы частиц (рис.4.6) найдем ее урав- нение моментов. Для каждой частицы системы, исходя из уравне-

ний (4.10)

�

�

dL = M,

dt

�

относительно неподвижно � й точки О имеем

dL 1 = d � t dL 2 = dt

 

M

внут

�

12

 

 

M

внут

�

+ M внеш,

�

+ M внеш.

Определим производную по времени момента импульса системы

частиц�. С уче�том�(4.20)�и (4.1�9) получим

dL = d(L1 + L2) = dL 1 + dL 2 =

 

�

внут +

�

внеш +

�

внут +

�

внеш =

dt dt

dt dt

M 12 M 1

M 21 M 2

� �

1 2

= M внеш + M внеш.

Обобщим этот результат на систему, состоящую из произвольно-

го числа частиц.

�

å

dL =

dt i

 

�

i

M внеш =

 

�

M внеш, (4.23)

т. е. производная по времени момента импульса системы частицы отно- сительно неподвижной точки О равна векторной сумме моментов внеш- них сил, приложенных к частицам системы (сравните с выражением (4.10) для одной частицы). Уравнения (4.23) называются уравнением моментов системы частиц. Из (4.23) следует закон сохранения момен-

та импульса системы част � иц: �

если M внеш = 0, то L = const, (4.24)

или � �

L (t 1) = L (t 2).

Если векторная сумма моментов внешних сил, действующих на час- тицы системы относительно неподвижной точки, равна нулю, то мо- мент импульса системы частиц остается постоянным (сравните с (4.11)). Если система изолирована (замкнута), т. е. на частицы систе- мы не действуют внешние силы, то суммарный момент этих сил ра- вен нулю и, следовательно, момент импульса изолированной системы частиц остается постоянным.

Отметим, что во всех случаях, когда момент импульса системы час- тиц постоянен, моменты импульса отдельных частиц, составляющих систему, могут меняться со временем. Проектируя на ось z векторные уравнения (4.20,4.23) получим

Lz = å Liz, (4.25)

i

dLz = M внеш. (4.26)

dt z

z

Здесь Lz – момент импульса системы частиц относительно неподвиж- ной оси, а M внеш – сумма моментов внешних сил, действующих на сис- тему частиц относительно неподвижной оси. Уравнение (4.26) назы- вается уравнением моментов системы частиц относительно неподвиж- ной оси. Из (4.26) следует закон сохранения проекции момента импульса системы частиц (сравните с (4.17)):

если M внеш = 0, то L = const, (4.27)

или

z z

Lz (t 1) = Lz (t 2).

Если алгебраическая сумма моментов внешних сил, действующих на все частицы системы относительно некоторой неподвижной оси равна нулю, то момент импульса системы частиц относительно этой оси остается постоянным.

 

Вопросы и задания для самопроверки

1. Докажите, что сумма всех внутренних сил системы частиц рав- на нулю.

2. Докажите, что сумма моментов внутренних сил равна нулю.

3. Запишите уравнение моментов импульса системы частиц.

4. Запишите уравнение моментов импульса системы частиц от- носительно оси.

5. Сформулируйте закон сохранения момента импульса систе- мы частиц.

6. Как меняется со временем момент импульса замкнутой систе- мы частиц?

7. Могут ли меняться со временем моменты импульса частиц, со- ставляющих замкнутую систему?

 

ЦЕНТР МАСС СИСТЕМЫ ЧАСТИЦ

Центром инерции или центром масс систе- мы частиц называется точка С, радиус-вектор

rC

которой � определяется формулой

� 1 �

 

 

где

rC = å miri, (4.28)

m

i

m = å mi �

(4.29) z

— масса системы части i ц, а тор i частицы (рис. 4.7).

ri – радиус-век-

rC

Декартовы координаты точки центра масс (или проекции радиус- вектора �) в некоторой инерциальной системе отсчета имеют вид

x = 1 å m x, y = 1 å m y, z = 1 å m z. (4.30)

m

m

m

i i C i i i i

i i i

Если число частиц системы и их масса не меняются со временем,

то скорость точки центра масс � определяется как

� vC �

= = (å

m

p

v � drC d 1 �) = 1 å m dri = 1 å

 

� = 1 å�

= 1 �,(4.31)

i

i

i

C dt

m r

dt m i i

m i dt m mivi i m p

p pi

i

где � = å�

— импульс системы частиц. Следовательно, можно за-

писать i

� �

=

p mvC, (4.32)

т. е. импульс произвольной системы частиц в любой инерциальной систе- ме отсчета равен произведению массы системы на вектор скорости ее центра масс. Определим ускорение центра масс системы как

�

�

aC =

dvC

dt

. (4.33)

Продифференцируем импульс системы � (4.32) по времени с уче-

� � p

C C

том определений v (4.31) и a (4.33)

� � � 2 �

dp = dmvC = m dvC = m d rC = �.

dt dt

dt dt 2

maC

При рассмотрении закона сохранения импульса показано, что

если � – импульс системы частиц, то

� �

p �

dp =å F внеш = F внеш.

dt i

Тогда получаем уравнение движения центра масс

2 � �

� d rC

 

внеш

maC = m dt 2 = F

. (4.34)

Из этого уравнения видно, что центр масс произвольной системы движется так, как двигалась бы частица, масса которой равна сумме масс частиц системы, на которую действует сила, равная сумме внеш- них сил, приложенных к частицам системы. Отметим, что совершен- но не важно, к каким частицам системы приложены внешние силы. Таким образом, движение центра масс описывает движение произ- вольной системы частиц в целом. Рассмотрим несколько примеров движения центра масс различных систем.

 

Прыжок кошки

Если кошка прыгает горизонтально (рис. 4.8), то ее центр масс перемещается так же, как перемещается камень (материальная точ- ка) равной массы, брошенный горизонтально с той же высоты и с той же начальной скоростью. На кошку и камень в полете действу- ет одна и та же внешняя сила тяжести (трением о воздух пренебре-

гаем). Поэтому

� � �

maC = F = mg.

внеш

За счет внутренних сил кошка может только менять положение частей своего тела (кувыркаться), но не может изменить положение своего центра масс. Так же как и камень, центр масс кошки движет- ся в поле тяжести земли по параболе.

y

Рис. 4.8

 

Движение человека

При отсутствии сил трения че- ловек (рис. 4.9) не мог бы двигать- ся в горизонтальной плоскости, так как в этом случае сумма про- екций всех приложенных к чело- веку внешних сил (тяжести и нор-

мальной составляющей реакции x

опоры) на любую горизонтальную ось равна нулю. Следовательно,

ma = F внеш = N + P = 0.

Cx x x x

За счет внутренних сил чело-

Рис. 4.9

век, как и кошка, может только изменить положение частей своего тела (ног, рук), но не положение своего центра масс. При ходьбе или беге человек выносит одну ногу вперед, приподнимая ее над зем- лей, чтобы исключить действие на нее силы трения. Другая нога дви- жется назад. Ей препятствут сила трения, приложенная к человеку и направленная вперед по его движению. Эта сила и есть та внешняя сила, которая позволяет центру масс человека перемещаться в нуж- ном направлении.