
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Силы гравитационного взаимодействия
Гравитационное взаимодействие проявляется в притяжении друг к другу тел. Объясняется это взаимодействие наличием гравитацион- ного поля вокруг каждого тела. Модуль силы гравитационного взаимодействия FG между дву- мя материальными точками определяется законом всемирного тя- готения F = F = F = G m 1 m 2, (2.17)
G 1,2 2,1 r 2 где F 1,2, F 2,1 — силы взаимодействия, направленные вдоль прямой, со- единяющей материальные точки (см. п.2.5), G = 6,67 · 10–11 Нм2/кг2 — гравитационная постоянная, m 1, m 2, r — массы точек и расстояние между ними. Закон всемирного тяготения справедлив не только для матери- альных точек, но и для тел со сферически-симметричным распреде- лением масс, а также тел произвольной формы, размеры которых во много раз меньше расстояний между ними.
Сила тяжести Если принять одно из взаимодействующих тел Землю, а второе — тело с массой m, находящееся вблизи или на её поверхности, то тело притягивается с силой
(2.18) где M3, R3 — масса и радиус Земли.
R 2 в формуле (2.18) есть постоянная величина
имеет размерность ускорения и называется ускорением свободного па- дения. Сила тяжести — сила гравитационного притяжения Землей тела массой m
F тяж = mg. (2.19)
В отличие от силы FG модуль зависит от географической ши-
роты места расположения тела на Земле. На полюсах F тяж = mg, а на экваторе уменьшается на 0,36 %. Это различие обусловлено тем, что Земля вращается вокруг своей оси и образует неинерциальную сис- тему отсчета. С удалением тела относительно поверхности Земли на высоту h уменьшается сила тяжести
F тяж = mgn = (R + h)2, где, g = G × M 3 — ускорение свободного падения на высоте h от h Земли.
(R 3+ h) Масса в формулах (2.17–2.19) характеризует гравитационное взаимодействие тел, является его мерой и называется гравитацион- ной. В настоящее время с высокой точностью установлено равенст- во инертной (см. 2.2) и гравитационной масс тела, поэтому их не раз- личают и обозначают одной буквой m.
Если подвесить тело или положить его на не- подвижную опору, оно будет покоиться отно- сительно Земли, так как сила тяжести уравнове- шивается силой реак- ции, действующей на тело со стороны опоры или подвеса.
Силы реакции
подвес Рис. 2.4 Сила реакции — сила, с которой действуют на данное тело другие тела, ограничивающие его движени�е. Сила нормальной реакции опоры N приложена к телу и направле- на перпендикулярно плоскости опоры.
� Сила реакции нити (подвеса) T приложена к телу и направлена вдоль нити (подвеса) (рис. 2.4).
Вес тела � Вес тела Q — сила, с которой тело давит на опору или растягива- ет нить подвеса и приложена к опоре или подвесу. В соответствии с третьим законом Ньютона � � � �
Q = - T, � �
. Вес тела численно равен силе тяжести в том слу-
a a Возможны случаи, когда Q
когда Q = 0. Рассмотрим тело,
Движение вниз
Движение вверх находящееся в лифте, движущем- ся с ускорением (рис. 2.5). Рис. 2.5 На тело дей�ствуют две силы: ре- акции опоры N и сила тяжести F. Запишем второй закон Ньютона ma =
тяж
. (2.20)
вверх равенство (2.20) с учетом знака векторов сил и ускорения на ось X имеет вид ma = N 1 – F тяж = N 1 – mg, а при движении вниз –ma = N 2 – F тяж = N 2 – mg, где N 1 и N 2 — силы реакции опоры. Из последних равенств следу- ет, что N 1 = m (g + a), N 2 = m (g – a). Согласно определению веса тела Q 1 = N 1 и Q 2 = N 2 имеем при уско- ренном подъеме тела Q 1 > F тяж, а при ускоренном спуске Q 2 < F тяж. При спуске с ускорением a = g, Q = 0, тело находится в состоя- нии невесомости.
Силы трения Сила трения — результат взаимодействия поверхностей соприка- сающихся тел. Сила трения направлена по касательной к трущимся поверхностям в сторону, противоположную направлению относительного движения взаимодействующих тел. Различают внешнее (сухое) и внутреннее (вязкое) трение. Внешнее сухое трение возникает при относительном перемещении двух соприкасающихся тел и делится на:
— трение покоя; — трение скольжения; — трение качения. Перечисленным видам внеш- него трения соответствуют силы: покоя, скольжения, качения. Сила трения покоя
mg
F > F тел, когда величина внешних сил недостаточна, чтобы вызвать их относительное перемещение. Если к телу, находящемуся в соприкосновении с другим телом, F тр
g Рис. 2.6 тр. max приложить возрастающую внешнюю силу F, параллельную плоско- сти соприкосновения (рис. 2.6а), то при изменении F от нуля до не- которого значения F тр. max движения тела не возникает, что свидетель- ствует о неоднозначности силы трения покоя. Максимальная сила трения покоя F тр. max = m0 N, где m0 – коэффициент трения покоя, N — модуль силы нормальной реакции опоры. Коэффициент трения покоя m0 можно определить эксперимен- тально. Например, m0 = tga, где a – угол наклона к горизонту по- верхности опоры, с которой начинает скатываться тело под дейст- вием его силы тяжести.
При F > F тр. max происходит скольжение тел относительно друг дру- га с некоторой скоростью u (рис. 2.6б). � Сила трения скольжения направлена против скорости u. Модуль силы трения скольжения при малых скоростях движения вычисляет- ся в соответствии с законом Амонтона по формуле F тр = m N, (2.21) где m — безразмерный коэффициент трения движения, зависящий от материала и состояния поверхности соприкасающихся тел, и все- гда меньше m0.
Сила внутреннего трения воз- никает между слоями одного и того же сплошного тела (жид- кости или газа). Силы внут- реннего (вязкого) трения зави- сят от относительной скорости смещения отдельных слоев газа или жидкости друг относитель- но друга. Например, вязкое тре- ние возникает при течении жидкости или газа по трубам со скоро- стью u (рис. 2.7). Скорость слоев жидкости уменьшается при приближении их к стенкам трубы. Отношение разности скоростей Äu в двух близких слоях, расположенных на расстоянии Ä x, называется средним гра- диентом скорости. В одномерной задаче, когда u = u(х), средняя сила внутренне- го трения F вн.тр = h× s × Äu, (2.22) Ä x где h — коэффициент внутреннего трения, s — площадь взаимодей- ствующих слоев жидкости, Äu/Äх — средний градиент скорости. Коэффициент внутреннего трения зависит от агрегатного состоя- ния и температуры вещества.
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 794; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.42.196 (0.029 с.) |


 Соотношение G M 3
Соотношение G M 3
 �
�








 Q = - N, Q = N,
Q = - N, Q = N, � �
� � Q = T
Q = T

 чае, когда тело находится на гори- зонтальной поверхности опоры в состоянии покоя или равномерно-
чае, когда тело находится на гори- зонтальной поверхности опоры в состоянии покоя или равномерно-

 X го прямолинейного движения. �
X го прямолинейного движения. �
 больше или меньше и даже
больше или меньше и даже
 действу- ет между соприкасающимися по- верхностями взаимодействующих
действу- ет между соприкасающимися по- верхностями взаимодействующих а
а N υ б
N υ б Сила трения качения возникает тогда, когда тело, имеющее фор- му цилиндра или шара, катится по поверхности опоры. Численное значение силы трения качения определяется в соответствии с зако- ном Кулона по формуле
Сила трения качения возникает тогда, когда тело, имеющее фор- му цилиндра или шара, катится по поверхности опоры. Численное значение силы трения качения определяется в соответствии с зако- ном Кулона по формуле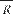 F тр.к = k,
F тр.к = k, где k — коэффициент трения качения имеет размерность длины и за- висит от материала соприкасающихся тел и состояния их поверхно- стей, R — радиус катящегося тела.
где k — коэффициент трения качения имеет размерность длины и за- висит от материала соприкасающихся тел и состояния их поверхно- стей, R — радиус катящегося тела. Рис. 2.7
Рис. 2.7


