
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Работа внешних сил при повороте твердого тела
T5.16 Кинетическая энергия вращательного движения тела вокруг неподвижной оси, равна 1) I w I 2w2
I w2
I 2w2
5) I w T5.17 Чему равна кинетическая энергия вращательного движе- ния тела, если момент инерции равен 5 кг· м2, а угловая скорость 4 рад/с. 1) 20 Дж 2) 10 Дж 3) 80 Дж 4) 40 Дж 5) 200 Дж T5.18 Полная кинетическая энергия диска, катящегося по гори- зонтальной поверхности равна 48 Дж. Определить кинетическую энергию поступательного и вращательного движения, если диск ка- тится без проскальзывания. 1) 32 и 16 Дж 2) 24 и 24 Дж 3) 8 и 40 Дж 4) 16 и 32 Дж 5) 40 и 8 Дж T5.19 Работа сил при вращательном движении тела вокруг непод- вижной оси (Miz –проекция на ось z момента i силы, действующей на тело, j — угол поворота тела) равна
iz ò iz ò 0 i 0 i 0 j j
iz ò iz 0 i 0 i T5.20 Закон изменения кинетической энергии тела, имеющего по- стоянный момент инерции, при вращательном движении имеет вид I w 2 I w 2 I w 2 I w 2 I w I w 1) A = 2 - 1 2 2 2) A = 2 + 1 2 2 3) A = 2 - 1 2 2 I w I w I 2w2 I 2w2 4) A = 2 + 1 2 2 5) A = 2 - 1 2 2 T5.21 Маховик начинает вращаться из состояния покоя с постоян- ным угловым ускорением 0,5 рад/c2. Определить кинетическую энер- гию маховика через 30 с после начала движения, если через 10 с после начала движения момент импульса маховика составлял 100 кг· м2/с. 1) 2000 Дж 2) 2250 Дж 3) 4000 Дж 4) 1350 Дж 5) 1000 Дж T5.22 Диск под действием постоянной силы достигает установ- ленной частоты вращения 33 об/мин через 1,5 оборотов после нача- ла движения. Чему равно его угловое ускорение? 1) 50p/243 рад/с2 2) 25p/243 рад/с2 3) 121p/600 рад/с2 4) –25p/243 рад/с2 5) –50p/243 рад/с2 T5.23 Диск массой 4 кг катится без скольжения по горизонталь- ной плоскости со скоростью 10 м/с. Найти кинетическую энергию диска. 1) 300 Дж 2) 200 Дж 3) 400 Дж 4) 100 Дж 5) 500 Дж
ЗАДАЧИ ДЛЯ КОНТРОЛЬНЫХ РАБОТ 5.1 Вывести формулу для момента инерции I диска массой m и радиу- сом R относительно оси, касающейся боковой поверхности диска и перпендикулярной его плоскости. 5.2 Вывести формулу для момента инерции I сплошного шара ра- диусом R и массой m относительно оси, касающейся поверхности шара.
5.3 Вывести формулу для момента инерции I полого шара относи- тельно оси, проходящей через его центр. Масса шара равна m, внут- ренний радиус — r, внешний — R.
5.4 Вывести формулу для момента инерции I цилиндрической муфты относительно оси, совпадающей с ее осью симметрии. Масса муфты равна m, внутренний радиус — r, внешний — R. 5.5 Определить момент инерции I сплошного однородного диска ра- диусом R = 40 см и массой m =1 кг относительно оси, проходящей че- рез середину одного из радиусов перпендикулярно плоскости диска. 5.6 Определить момент инерции I тонкого однородного стержня дли- ной l = 50 см и массой m = 360 г относительно оси, перпендикуляр- ной стержню и проходящей через: 1) конец стержня; 2) точку, отстоя- щую от конца стержня на 1/3 его длины. 5.7 Шар и сплошной цилиндр, изготовленные из одного и того же ма- териала (r1 = r2), одинаковой массы (m 1 = m 2) катятся без скольжения равномерно по горизонтальной поверхности с одинаковой скоростью (v 1 = v 2). Определить, во сколько раз кинетическая энергия шара T 1 меньше кинетической энергии сплошного цилиндра T 2. 5.8 Полная кинетическая энергия Т диска, катящегося по горизон- тальной поверхности, равна 24 Дж. Определить кинетическую энер- гию Т 1 поступательного и Т 2 вращательного движения диска. 5.9 Полый тонкостенный цилиндр массой m = 0,5 кг, катящийся без скольжения, ударяется о стену и откатывается от нее. Скорость ци- линдра до удара о стену v 1 =1,4 м/с, после удара — v 2 =1 м/с. Опреде- лить выделившееся при ударе количество теплоты Q. 5.10 К ободу однородного сплошного диска массой m = 10 кг, насажен- ного на ось, приложена постоянная касательная сила F = 30 Н. Оп- ределить кинетическую энергию диска через время t = 4 с после на- чала действия силы.
5.11 Шар радиусом R = 10 см и массой m = 5 кг вращается вокруг оси симметрии согласно уравнению j = A + Bt 2 + Ct 3 (B = 2 рад/с2, С = –0,5 рад/с3). Определить момент сил М для t = 3 с. 5.12 Вентилятор вращается с частотой n = 600 об/мин. После выклю- чения питания он начал вращаться равнозамедленно и, сделав N = 50 оборотов, остановился. Работа А сил торможения равна –31,4 Дж. Определить: 1) момент М сил торможения; 2) момент инерции I вен- тилятора. 5.13 Маховик в виде сплошного диска, момент инерции которо- го I =150 кг· м2, вращается с частотой n = 240 об/мин. Через время t = 1 мин, после того как на маховик стал действовать момент сил торможения, он остановился. Определить: 1) момент М сил тормо- жения; 2) число N оборотов маховика от начала торможения до пол- ной остановки.
5.14 Сплошной однородный диск скатывается без скольжения по на- клонной плоскости, образующей угол a горизонтом. Определить ли- нейное ускорение а центра диска. 5.15 К ободу однородного сплошного диска радиусом R = 0,5 м прило- жена постоянная касательная сила F = 100 Н. При вращении диска на него действует момент сил трения М тр = 2 Н· м. Определить мас- су m диска, если известно, что его угловое ускорение e постоянно и равно 16 рад/с2. 5.16 Частота вращения n 0 маховика, момент инерции I которого 120 кг· м2, составляет 240 об/мин. После прекращения действия на него вращающего момента маховик под действием сил трения в подшип- никах остановился за время t = p мин. Считая трение в подшипни- ках постоянным, определить момент М сил трения. 5.17 Маховик в виде сплошного диска, момент инерции которого I = 1,5 кг·м2, вращаясь при торможении равнозамедленно, за вре- мя t = 1 мин уменьшил частоту своего вращения с n 0 = 240 об/мин до
n 1 = 120 об/мин. Определить: 1) угловое ускорение маховика e; 2) мо- мент М и 3) работу силы торможения А. 5.18 Колесо радиусом R = 30 см и массой m = 3 кг скатывается по на- клонной плоскости длиной L = 5 м и углом наклона a = 25°. Опре- делить момент инерции колеса I, если его скорость v в конце движе- ния составляла 4,6 м/с. 5.19 С наклонной плоскости, составляющей угол a = 30° c горизон- том, скатывается без скольжения шарик. Определить время движе- ния шарика по наклонной плоскости t, если известно, что его центр масс при скатывании понизился на h = 30 см. 5.20 Полый тонкостенный цилиндр катится вдоль горизонтального участка дороги со скоростью v =1,5 м/с. Определить путь s, который он пройдет в гору до остановки, если уклон горы равен 5 м на каж- дые 100 м пути. 5.21 На однородный сплошной цилиндрический вал радиусом R = 50 см намотана легкая нить, к концу которой прикреплен груз массой m = 6,4 кг. Груз, разматывая нить, опускается с ускорением а = 2 м/с2. Определить: 1) момент инерции I вала; 2) массу М вала. 5.22 На однородный сплошной цилиндрический вал радиусом R = 5 см и массой М = 10 кг намотана легкая нить, к концу которой прикре- плен груз массой m = 1 кг. Определить: 1) зависимость s (t), соглас- но которой движется груз; 2) силу натяжения нити T; 3) зависимость j(t), согласно которой вращается вал; 4) угловую скорость w вала че- рез t = 1 с после начала движения; 5) тангенциальное (а t) и нормаль- ное (аn) ускорения точек, находящихся на поверхноcти вала. 5.23 На однородный сплошной цилиндрический вал радиусом R = 20 см, момент инерции которого I = 0,15 кг · м2, намотана легкая нить, к кон- цу которой прикреплен груз массой m = 0,5 кг. До начала вращения ба- рабана высота h груза над полом составляла 2,3 м. Определить: 1) вре- мя t опускания груза до пола; 2) силу натяжения нити F; 3) кинети- ческую энергию груза T в момент удара о пол.
5.24 Через неподвижный блок в виде однородного сплошного цилин- дра массой m = 0,2 кг перекинута невесомая нить, к разным концам которой прикреплены тела массами m 1 = 0,35 кг и m 2 = 0,55 кг. Пре- небрегая трением в оси блока, определить: 1) ускорение грузов a; 2) отношение Т 2/ Т 1 сил натяжения нити.
5.25 Тело массой m 1 = 0,25 кг, соединенное невесомой нитью посред- ством блока (в виде полого тонкостенного цилиндра) с телом массой m 2 = 0,2 кг, скользит по поверхности горизонтального стола. Масса блока m = 0,15 кг. Коэффициент трения μ тела о поверхность равен 0,2. Пренебрегая трением в подшипниках, определить: 1) ускорение а, с которым будут двигаться эти тела; 2) силы натяжения Т 1 и T 2 нити по обе стороны блока. 5.26 Колесная пара, состоящая из колес массой m = 400 кг и оси мас- сой M = 100 кг, катится по железнодорожному полотну со скоростью v = 4 м/с. Определить кинетическую энергию T колесной пары. Счи- тать колеса дисками, а ось — стержнем. 5.27 Обруч и сплошной цилиндр одинаковой массы m = 5 кг катятся без скольжения с одинаковой скоростью v = 10 м/с. Найти кинети- ческие энергии T 1 и T 2 этих тел. 5.28 Маховик делает n =100 об/с. Под действием постоянного тормо- зящего момента, равного M = 196 Н· м, он остановился через t = 50 с. Определить момент инерции I маховика. 5.29 Однородный шар радиусом r = 20 см скатывается без скольжения с вершины сферы радиусом R = 50 см. Определить угловую скорость w шара после отрыва от поверхности сферы. 5.30 Маховик начинает вращаться из состояния покоя с постоянным угловым ускорением e = 0,4 рад/с2. Определить кинетическую энер- гию маховика T через время t 2 = 25 с после начала движения, если через t 1 =10 с после начала движения момент импульса L маховика составлял 60 кг· м2/с.
5.31 Горизонтальная платформа массой m = 25 кг и радиусом R = 0,8 м вращается с частотой n 1=18 мин–1. В центре стоит человек и держит в разведенных руках гири. Считая платформу диском, определить час- тоту вращения платформы n 2, если человек, опустив руки, уменьшит свой момент инерции от I 1 = 3,5 кг· м2 до I 2 = 1 кг· м2. 5.32 Человек, стоящий на скамье Жуковского, держит в руках стержень длиной l = 2,5 м и массой m = 8 кг, расположенный вертикально вдоль оси вращения скамейки. Эта система (скамья и человек) обладает моментом инерции I =10 кг· м2 и вращается с частотой n 1 =12 мин–1. Определить частоту n 2 вращения системы, если стержень повернуть в горизонтальное положение. 5.33 Человек массой m = 60 кг, стоящий на краю горизонтальной плат- формы массой М = 120 кг, вращающейся по инерции вокруг непод- вижной вертикальной оси с частотой n 1 = 10 мин–1, переходит к ее центру. Считая платформу круглым однородным диском, а челове- ка — точечной массой, определить, с какой частотой n 2 будет вра- щаться платформа.
5.34 Платформа, имеющая форму сплошного однородного диска, мо- жет вращаться по инерции вокруг неподвижной вертикальной оси c угловой скоростью w0. На краю платформы стоит человек, масса ко- торого m в 3 раза меньше массы платформы M. Определить, как и во сколько раз изменится угловая скорость вращения платформы w/w0, если человек перейдет ближе к центру на расстояние l, равное поло- вине радиуса платформы R. 5.35 Человек массой m = 60 кг, стоящий на краю горизонтальной плат- формы радиусом R = 1 м и массой M = 120 кг, вращающейся по инер- ции вокруг неподвижной вертикальной оси с частотой n 1 = 10 мин–1, переходит к ее центру. Считая платформу круглым однородным дис- ком, а человека — точечной массой, определить работу A, совершае- мую человеком при переходе от края платформы к ее центру.
|
||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 841; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.131.110.169 (0.032 с.) |
 2)
2) 3)
3) 4)
4)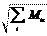 -j j j
-j j j


