
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Затухающие механические колебания
В реальных условиях механические колебания происходят в среде. Взаимодействие колеблющейся системы со средой приводит к рас- сеиванию (диссипации) энергии колебаний (механическая энергия колебаний превращается во внутреннюю энергию среды). Колеба-
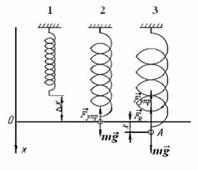
Переход от одного максималь- Рис. 6.11 ного значения физической величи- ны до следующего максимального значения по абсолютной величине, деленное пополам, назовем ампли- тудой колебания. При затухающих колебаниях амплитуды уменьшают- ся, но время прохождения соседних амплитуд остается постоянным. За условный период затухающих колебаний принимается про- межуток времени двух переходов от одного крайнего положения до другого. Найдем уравнение затухающих колебаний груза массой m, подве- шенного на пружине, с коэффициентом упругости k. На рис. 6.11 по- казаны три состояния системы. Состояние 1 — естественная длина пружины. Состояние 2 — груз висит на пружине, система находится в со- стоянии статического равновесия.
� � ' mg + F упр =0. (6.34) Начало координат совмещено с состоянием статического равно- весия, так как любое колебание происходит около положения рав- новесия. Ä x — статическая деформация. Из проекции уравнения (6.34) на ось Х с учетом того, что модуль силы упругости равен k Ä x, получим mg = k Ä x. (6.35) Для удобства составления дифференциального уравнения состоя- ние 3 (рис. 6.11) зафиксировано в тот момент движения груза, когда деформация пружины х увеличивается и груз движется вниз. Пусть груз движется со скор�остью, меньшей 20 м/с. В этом случае сила со- п�ротивления среды FR пропорциональна первой степени скорости
казывает, что сила сопротивления среды направлена в сторону, про- тивоположную движению, т. е. в данном случае вверх. Модуль силы сопротивления равен
R dt � На�рис. 6.11 показаны силы mg,
� F упр � и FR . Модуль силы упруго- сти F упр пропорционален сумме статической Ä x и динамической x деформации, т. е. F упр = k (Ä x + x). Запишем второй закон Ньютона применительно к грузу, находя- щемуся в состоянии 3. (см. рис. 6.11). � � � � mg + F упр + FR = ma. (6.36) Проекция векторного уравнения на ось x равна mg - k (Ä x + x) - r v = ma, (6.37) d 2 x dx 1
d 2 x + r dx + k = dt 2 m dt x 0. (6.38) m Введя обозначения k = w2 и r = 2b, перепишем последнее урав- нение в виде
m 0 m d 2 x
+ 2b dx
+ w2 x = 0. (6.39) Для решения уравнения (6.39) воспользуемся методом Эйлера. Ре- шение ищем в виде x = Ce a t, где C — произвольная константа, a — неизвестная константа. Для нахождения констант подставим
dx = C a e a t dt d 2 x
= C a2 e a t в (6.39), получим тождество В полученном тождестве один из сомножителей должен равнять- ся нулю. 1. C ¹ 0, так как рассматривается движение, а не покой; 2.
a1,2 = -b ± В зависимости от соотношения w0 и b возможны 3 различных ва- рианта возвращения системы в состояние равновесия. 1 вариант Если b > w0, то корни a1 и a2 — действительные и разные. В этом случае нет колебательного движения, так как показатель степени e a t — вещественное число. Действительно, каждому корню характеристического уравнения соответствует по методу Эйлера частное решение вида:
0⎟⎠,
0⎟⎠.
Тогда общее решение находится как линейная комбинация част- ных решений
или x (t) = C 1 x 1 + C 2 x 2
0⎟⎠ + C e ⎜⎝ 0⎟⎠
Так как b > , то степенная функция со временем убывает.
туации приведены на рис. 6.12. Если х 0 > 0, начальная ско-
ния равновесия, то зависимость x (t) имеет вид а на рис. 6.12. Если х 0 > 0, начальная ско-
направлена к положению рав- новесия, то груз один раз мо- жет пересечь положение рав- новесия, а затем устремиться к нему. Зависимость x (t) име- ет вид б на рис. 6.12. Если х 0 > 0, начальная ско-
положению равновесия, то за- висимость x (t) имеет вид в на рис. 6.12. 2 вариант
Рис. 6.12 Если b = w0, то корни a1,2 = -b, т. е. корни a1 иa2 являются крат- ными. Частные решения одинаковы и равны e a t. В этом случае, чтобы не потерять одно частное решение, вместо постоянных интегрирования С 1 и С 2, следует записать многочлен, сте- пень которого на единицу меньше кратности корня характеристиче- ского уравнения. Общее решение запишется в виде
Поскольку многочлен (С 1 + t C 2) растет намного медленнее, чем убывает сомножитель e -b t, то функция x (t) будет близка к видам а, б, в, приведенным на рис. 6.12. Вывод. При b ³ w0 движение груза перестает быть периодическим, т. е. система возвращается в равновесное состояние без колебательно- го процесса. Это может иметь место тогда, когда, например, сила со- противления среды больше силы упругости пружины. Такой характер движения называют апеpиодическим затуханием. 3 вариант
= -b ± = -b ± i = -b ± i w, где i — мнимое число, w = — циклическая частота затухаю- щего колебания. Такая ситуация имеет место тогда, когда сила сопро- тивления среды меньше силы упругости пружины, т. е. F упр > FR. Каждому значению корня a1,2 соответствует частное решение. Об- щее решение находится как линейная комбинация двух частных ре- шений:
= e -b t ⎡cos w t (C * + C *) + sin w t (iC * - iC *)⎤. ⎣ 1 2 1 2 ⎦ Переобозначив константы C = C * + C *, C = iC * - iC *, получим 1 1 2 2 1 2
Так как C 1 cos w t + C 2 sin w t = A 0 cos(w t + j0) то (см. параграф 6.3.1),
Собственные затухающие колебания маятника периодические, но не являются гармоническими, так как амплитуда таких колебаний с течением времени уменьшается по экспоненте где b — коэффициент затухания.
Условный период затухающих колебаний равен Рис. 6.13
w . (6.42) Условный период затухающих колебаний — наименьший проме- жуток времени Т, за который колеблющийся груз дважды проходит через положения равновесия, двигаясь в одном и том же направлении. Период затухающих колебаний груза больше периода незатухающих колебаний этого же груза, так как силы сопротивления тормозят дви- жение; тело возвращается к равновесному состоянию медленнее.
На рис. 6.13 сплошной линией показана зависимость x = x (t), штриховая линия проведена по максимальным значениям амплиту- ды затухающих колебаний.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 524; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.154.171 (0.054 с.) |
 ния затухают. Затухающие колеба- ния не являются периодическими, так как через конечный промежу- ток времени физическая величи- на не принимает то же значение. Однако через равные промежутки времени повторяются максималь- ные, но разные по абсолютной ве- личине отклонения величины от положения равновесия.
ния затухают. Затухающие колеба- ния не являются периодическими, так как через конечный промежу- ток времени физическая величи- на не принимает то же значение. Однако через равные промежутки времени повторяются максималь- ные, но разные по абсолютной ве- личине отклонения величины от положения равновесия. F = r v = r dx.
F = r v = r dx.

 где mg = k Ä x, a =, v =. Умножив уравнение (6.37) на, по- лучим dt 2 dt m
где mg = k Ä x, a =, v =. Умножив уравнение (6.37) на, по- лучим dt 2 dt m



 dt 2
dt 2 dt
dt x = Ce a t,
x = Ce a t, , dt 2
, dt 2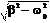 Из этого уравнения, именуемого характеристическим, найдем не- известную константу a:
Из этого уравнения, именуемого характеристическим, найдем не- известную константу a: ⎛-b+ b2 -w2 ⎞ t
⎛-b+ b2 -w2 ⎞ t ⎛-b- b2 -w2 ⎞ t
⎛-b- b2 -w2 ⎞ t

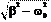 где С 1 и С 2 — произвольные константы. Проанализируем зависимость x (t).
где С 1 и С 2 — произвольные константы. Проанализируем зависимость x (t).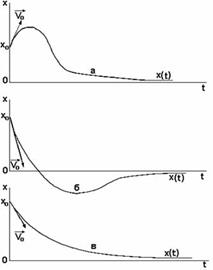 v 0
v 0
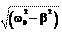 Если w0 > b, то корни a1 иa2 комплексные и принимают значения
Если w0 > b, то корни a1 иa2 комплексные и принимают значения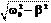 a1, 2
a1, 2 График затухающих колебаний x (t) показан на рис. 6.13. Зависи- мость x (t) не выходит за пределы
График затухающих колебаний x (t) показан на рис. 6.13. Зависи- мость x (t) не выходит за пределы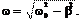 Циклическая частота затухаю- щих колебаний w связана с собст- венной частотой пружинного ма- ятника w0 соотношением
Циклическая частота затухаю- щих колебаний w связана с собст- венной частотой пружинного ма- ятника w0 соотношением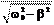 T = 2p = 2p
T = 2p = 2p


