
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы механики твердого телаСтр 1 из 51Следующая ⇒
Фишбейн Л.А. 5.1. Динамика твердого тела....................................................................... 277 5.2. Условия равновесия твердого тела..................................................... 278 5.3. Поступательное движение твердого тела........................................... 287 5.4. Вращение твердого тела вокруг неподвижной оси. Момент инерции твердого тела. Теорема Штейнера......................... 288 5.5. Закон сохранения момента импульса системы твердых тел при их вращении вокруг неподвижной оси.................. 303 5.6. Кинетическая энергия твердого тела, вращающегося вокруг неподвижной оси. Работа внешних сил при повороте твердого тела................................................................. 307 5.7. Плоское движение твердого тела........................................................ 312 5.8. Кинетическая энергия тела при плоском движении.......................... 314 Основные положения................................................................................... 319 Обозначения, используемые в главе 5....................................................... 320 Тесты для электронного экзамена.............................................................. 321 Задачи для контрольных работ................................................................... 324 Глава 6 МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ Хан Е.Б. 6.1. Понятие колебательного движения.................................................... 330 6.2. Кинематика механических гармонических колебаний...................... 331 6.3. Динамика механических гармонических колебаний.......................... 337 6.3.1. Пружинный маятник.................................................................. 338 6.3.2. Физический маятник.................................................................. 342 6.3.3. Математический маятник.......................................................... 344 6.4. Сложение однонаправленных колебаний одинаковой частоты............................................................................. 351 6.5. Сложение взаимно перпендикулярных гармонических колебаний.................................................................... 354 6.6. Затухающие механические колебания................................................ 358 6.7. Вынужденные механические колебания............................................. 368 6.8. Механические волны............................................................................ 376 6.8.1. Общие сведения о механических волнах.................................. 376 6.8.2. Виды волн................................................................................... 381 6.8.3. Уравнение плоской гармонической волны.............................. 382 6.8.4. Интерференция волн.................................................................. 386 6.8.5. Стоячие волны........................................................................... 387
Основные положения................................................................................... 396 Обозначения, используемые в главе 6....................................................... 401 Тесты для электронного экзамена.............................................................. 402 Задачи для контрольных работ................................................................... 409 Указания к выполнению контрольной работы.......................................... 430 Таблица заданий по контрольной работе № 1............................................ 432 Таблица заданий по контрольной работе № 2............................................ 434 Греческое слово «ta jusica» означает наука о природе.
ВВЕДЕНИЕ Физика — наука о наиболее общих законах движения материи. Она единственная среди естественных наук имеет предметом своего изучения весь окружающий нас мир, позволяя объяснить его с еди- ных позиций. Определение физики дает возможность уяснить, почему она играет столь большую роль в современном естествознании. На- капливая знания, физика постоянно расширяет свои традиционные области исследования. Это приводит к ее прямому проникновению в другие науки и даже порождает новые, такие, как физикохимия, гео- физика, биофизика, медицинская физика, агрофизика и т. д. Физика выросла из потребностей техники и непрерывно исполь- зует ее опыт. Еще вчера законы микромира были областью интере- сов исключительно группы физиков, а сегодня — предмет препода- вания в курсе инженерных наук любого технического вуза. Используя все более тонкие физические явления и процессы, техника достигла невиданных ранее возможностей. Взаимосвязь физики и техники — основной путь развития и той и другой. Нынешний этап в развитии физики характеризуется быстрым со- кращением времени между открытием новых закономерностей и их использованием в других областях науки и техники. Если раньше на это уходили десятилетия, то теперь годы, а то и месяцы. Скорость, с которой физические теории становятся основой инженерных рас- четов, требует постоянного усовершенствования процесса препода- вания физики. Очевидно, что только фундаментальные знания не подвержены старению и могут подготовить специалиста к воспри- ятию новейших технологий, определяющих технический прогресс общества.
Все это ставит среднюю и особенно высшую школу перед слож- ной проблемой организации обучения. Поиски касаются разработ- ки учебных планов, программ, учебников и учебных пособий. Обуче- ние, следуя логике развития науки, непрерывно меняет свои формы
и, ломая традиции, ищет наиболее эффективные способы, позво- ляющие быстро передать новому поколению запас знаний, накоп- ленный физической наукой. Два существенных обстоятельства мешают прогрессу в этой об- ласти. Во-первых, наличие огромного фактического материала затрудняет выбор того необходимого минимума, без которого невоз- можно перейти к изучению специальных дисциплин. Во-вторых, ог- ромную трудность представляет глубокий разрыв между значением современной физики и уровнем подготовки студентов к ее воспри- ятию в высшей школе. Предлагаемое вниманию читателей издание по курсу общей фи- зики состоит из трех частей: «Механика», «Электродинамика», «Оп- тика, квантовая физика и физика твердого тела». В первой части изучается простейшая форма движения материи — механическое движение, т. е перемещение одних тел или частей тела относитель- но других. Вторая посвящена изучению движения и взаимодействия электрических зарядов. Третья описывает распространение электро- магнитного излучения (света) и его взаимодействие с веществом, движение микроскопических частиц и физику твердого состояния вещества. Пособие разработано на основе современных образовательных программ по физике для высшей школы, с учетом сложившихся под- ходов к образовательному процессу и контролю знаний и предназна- чено для студентов заочной и дистанционной форм обучения, нахо- дящихся в наименее благоприятной (по сравнению с очной формой) образовательной среде. Цель авторов книги — дать представление об основных физи- ческих явлениях и важнейших физических законах. Учитывая ост- рую нехватку учебных часов, авторы стремились, сохраняя главное и по возможности опуская второстепенные детали, провести тща- тельную систематизацию и структурирование материала, четко обо- значив функциональные связи между его различными частями, оп- тимизировать изучение различных разделов курса и провести увязку фундаментальных проблем физики с профессиональной подготов- кой студентов. Достоинством пособия является тщательная методи- ческая проработка, способствующая минимизации усилий студентов для получения максимума полезной физико-математической инфор-
мации, многообразие и широкий спектр рассматриваемых вопросов. Теоретический материал в достаточной и доступной форме знакомит студента с основными физическими явлениями и закономерностя- ми. Значительное внимание в тексте уделяется решению задач, мно- гие из которых сопровождаются подробным анализом и развернуты- ми комментариями. Представленные примеры решения задач спо- собствуют развитию аналитических способностей студентов, умению воспринимать общие физические закономерности через их конкрет- ное, частное проявление, а также обеспечивают более качественный самоконтроль и облегчают поиск ошибок при самостоятельном ре- шении физических задач. Изучение определенного раздела пособия необходимо начать с тщательной проработки теоретического материала и последующих ответов на вопросы соответствующих параграфов. Далее следует пе- рейти к анализу решенных в пособии задач. Сначала попытаться по- лучить ответ самостоятельно и сравнить свое решение с приведенным. Если при самостоятельном подходе возникают затруднения, следует детально разобрать образец решения. Достаточно подробные объяс- нения позволяют понять методику решения задачи. В целом решение физических задач является важнейшей составляющей изучения физи- ки. При этом цель состоит не в том, чтобы решить ту или иную кон- кретную задачу, написать контрольную работу, сдать экзамен и т. д., а развить в себе физическую интуицию и выработать определенную технику и методологию. Последнее и определяет уровень образова- ния, его фундаментальность. В сознании обычно остаются не фор- мулы и схемы, а лишь принципы и методы, используя которые, мож- но искать решения тех или иных практических задач.
Работу над контрольными заданиями, определяемыми учебным планом, начните с тестов — часто наиболее простых одноходовых задач, для решения которых достаточно знания основных законов данного раздела и их аналитических выражений. Близкие по физи- ческому содержанию тесты будут предложены вам на электронном экзамене. К сожалению, нельзя сформулировать единый алгоритм правиль- ного решения задач (и тестов), так как они очень разнообразны и мно- гоплановы. Решайте как можно больше задач, переходя от простых к более сложным, не пренебрегайте повторным анализом уже решен-
ных задач. Последнее способствует запоминанию физических законов и более глубокому осознанию их сущности, позволяет натренировать- ся в применении физических формул и математических преобразова- ний. При решении физических задач руководствуйтесь следующим: — внимательно изучите условие задачи, пытаясь понять физиче- скую сущность явлений и процессов, рассматриваемых в ней, уясни- те основной вопрос задачи; — выделите заданные и неизвестные величины, кратко запиши- те условия задачи, переведите значения необходимых величин в сис- тему СИ; — сделайте рисунок, схему или чертеж, указав все необходимые величины; — установите физические закономерности, позволяющие опи- сать рассматриваемую в задаче ситуацию, и запишите их в матема- тической форме; — введите удобную систему координат; — запишите уравнение или систему уравнений, связывающих из- вестные и неизвестные параметры задачи;
— найдите искомые величины в общем виде, проведя необходи- мые алгебраические преобразования; — проверьте правильность решения с помощью размерностей фи- зических величин — с правой и с левой сторон равенства должны по- лучаться одинаковые размерности; — подставьте в общее решение числовые значения величин и про- изведите расчеты с учетом правил приближенных вычислений; — оцените правильность полученного результата; — запишите ответ в единицах системы СИ (или в тех единицах, которые в большей степени соответствуют смыслу задачи). Для того чтобы успешно сдать экзамен по физике, студенту не- достаточно иметь хорошую теоретическую подготовку и уметь ре- шать физические задачи. Часто причина неудачи — слабые матема- тические навыки, отсутствие внимательности, аккуратности и соб- ранности. Укажем на некоторые недостатки, встречающиеся на экзаменах по физике: — формализм знаний, нечеткое и поверхностное понимание фи- зических законов;
— неправильное понимание условия задачи; — проявление невнимательности при краткой записи условия за- дачи (использование отсутствующих физических параметров или не- правильное толкование имеющихся); — отсутствие навыков перевода физических величин из одних единиц в другие; — незнание основ дифференциального исчисления и элементар- ных правил векторной алгебры; — неумение проводить алгебраические преобразования и ариф- метические вычисления, решать квадратные уравнения, работать с показателями степеней и т. д.; — некритическое отношение к результатам, неумение выбирать из полученных решений правильные ответы, соответствующие фи- зическим условиям задачи. В пособии принята сквозная нумерация формул, рисунков, при- меров решения задач, тестов и контрольных задач. Первое число со- ответствует номеру главы, второе число — порядковому номеру фор- мулы, рисунка и т. д. Для работы с книгой помимо владения алгеброй и тригонометри- ей необходимо знакомство с элементами дифференциального и ин- тегрального исчисления, а также векторной алгебры. Если же сту- дент обладает недостаточными математическими навыками, то на- чать работу с книгой следует с математического введения. Помните, что изучить физику за несколько недель невозможно. Для успешно- го овладения и, что самое главное, возможности применения физи- ческих идей при дальнейшем обучении и в профессиональной дея- тельности необходима регулярная, повседневная работа — длитель- ные размышления над изучаемыми проблемами. Авторы надеются, что изучение материалов пособия окажет заин- тересованным студентам большую помощь в овладении курсом фи- зики, создаст у них определенное представление об уровне экзаме- национных требований и будет способствовать дальнейшему успеш- ному обучению в вузе.
МАТЕМАТИЧЕСКОЕ ВВЕДЕНИЕ ВЕКТОРНАЯ АЛГЕБРА Вектором называется направленный отрезок, для которого зада- ны длина, называемая модулем или величиной вектора, и направле- ние. Скалярной величиной, или скаляром, называется число, то есть ве-
личина, не�обладающая направлением. Сила F, действующая на материальную точку, есть вектор, так как она обладает направлением. В курсе физики вы познакомитесь с такими векторными величинами, как скорость �, ускорение �, им- � � � v a пульс p, момент и�мпульса L, момент силы� M, напряженность элек- трического поля E, магнитная индукция B и т. д. Температура тела T есть скаляр, так как с этой числовой величи- ной не связано никакое направление. Масса тела m и его плотность r — тоже скаляры. Над векторами производят действия, называемые сложением, вы- читанием и умножением векторов.
СЛОЖЕНИЕ ВЕКТОРОВ
� и b, то их можно сложить по правилам
� � �
c = a + b. (1.1) Рис. 1.1 Рис. 1.2
параллелограмма, построенного на составляющих векторах как на сто- cy ронах (начала всех трехвекторов совпадают). Во втором случае по- ступают так: с концом вектора � � a Рис. 1.3 совмещают начало вектора b. Со- единив затем начало первого векто-
Составляющей вектора вдоль пря- мой (плоскости) называется век- тор, лежащий на данной прямой (плоскости), начало и конец ко- торого совпадают с проекциями начала и ко�нца в�ектора. На рис. 1.3 � � � ax и аy —�это составляющие вектора a, а bx и by — составляющие вектора b. Проекцией вектора на ось называется скаляр (число), рав- ный по величине модулю составляющей вектора на ту же ось, причем это число берется со знаком плюс, если направление составляющей вектора совпадает с направлением оси, и со знаком минус, если эти направления противоположны. Проекции суммарного вектора на ко- ординатные оси равны сумме проекций слагаемых векторов
сx = ax + bx, сy = ay + by. (1.2) Это видно из рисунка 1.3.
УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО
b = n �, имеющий то же направление, что и вектор �, но модуль в n a a раз больший, если n ³ 1, и м�одуль в 1/ n раз меньший, если 0 £ n £ 1 (рис. 1.4). Модуль вектора b равен b = | n | a, а проекция вектора b равна bx = nax.
Если вектор умножить на отрицательное число k (k < 0), то по- лучится вектор �= k �, направленный противоположно вектору �, с c a a
| k | если 0 £ | k | £ 1 (рис. 1.5). Модуль вектора � равен с = | k | a, а проекция c
ВЫЧИТАНИЕ ВЕКТОРОВ Вычесть из вектора � � вектор (рис. 1.6) — значит прибавить к � � a b �
минус указывает здесь противоположность направления): � = � – � = � + (- �).
�
Можно находить разность векторо�в ина-
Рис. 1.6
и b выходящими из одной точки � (рис. 1.7), то разность векторов изобрази�тся вектором с, проведен-
таются и их проекции�на координат- ные оси. Если � = � - b, то с = a – b Рис. 1.7 c a (рис. 1.8). x x x
1.4. Прямоугольными координатами век- тора � называются проекции векто- � a Рис. 1.8 ра a на оси координат (рис. 1.9). Ко- ординаты вектора обозначаются бук- вами ax, ay, az. Запись: � a = { ax, ay, az }. (1.3)
Векторы i, � � j, k, изображенные на рисунке, называются единичными ортами (единичными векторами) ко- ординатных осей. Их модули равны единице, а направления совпадают с направлением осей ОX, ОY и ОZ. Зная
Рис. 1.9 вить его как � � � � a = ax i + ay j + az k. (1.4)
ДЛИНА ВЕКТОРА Длина вектора � = { с, с, с } выражается через его координаты по c x y z теореме Пифагора формулой
После нахождения вектора �, являющегося суммой векторов � � c a
т. е. его длины. Возможны следующие случаи:
1.
b). В этом случае от векторной записи � � �
Рис. 1.10 c = a + b (1.6)
OX: с = a + b. (1.7) 2. лены (�¯ b). Спроектиро-
Рис. 1.11 вав уравнение c = a + b на ось OX (рис. 1.11), получаем OX: – с = a – b. (1.8) 3.
теореме Пифагора, записанной для пря�мо- угольного треугольника ODE. ⎪ ОD ⎪ = ⎪ b ⎪ и ⎪ DЕ ⎪=⎪ � ⎪ — катеты треугольника, ⎪ ОЕ ⎪ =
a — его гипотенуза. Поэтому
Рис. 1.12
4.
Рис. 1.13
шется как
с 2 = а 2 + b 2 - 2 × а × b × cosa. (1.10)
a = 180° - b. Так как cos (180° - b) = -cosb, выражение (1.10) можно записать в следующем виде: с 2 = а 2 + b 2 + 2 × а × b × cosb. (1.10)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 426; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.208.183 (0.122 с.) |

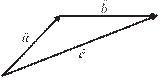










 Рис. 1.4 Рис. 1.5
Рис. 1.4 Рис. 1.5 модулем в | k | раз большим, если | k | ³ 1, и модулем в 1 раз меньшим,
модулем в | k | раз большим, если | k | ³ 1, и модулем в 1 раз меньшим, вектору a вектор (- b), отличающийся от вектора b тем, что он на- правлен в противоположную сторону (знак
вектору a вектор (- b), отличающийся от вектора b тем, что он на- правлен в противоположную сторону (знак Модули векторов b и (- b)равны, а их
Модули векторов b и (- b)равны, а их направления противоположны (такие век- торы называются противоположными). Проекции противоположных векторов име- ют противоположные знаки. Сами же век-
направления противоположны (такие век- торы называются противоположными). Проекции противоположных векторов име- ют противоположные знаки. Сами же век- торы не могут быть ни положительными, ни отрицательными.
торы не могут быть ни положительными, ни отрицательными. При вычитании векторов вычи-
При вычитании векторов вычи-
 КООРДИНАТЫ ВЕКТОРА
КООРДИНАТЫ ВЕКТОРА �
�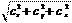 . (1.5)
. (1.5)
 легко перейти к скалярной, спроектировав уравнение (1.6) на ось OX (рис. 1.10)
легко перейти к скалярной, спроектировав уравнение (1.6) на ось OX (рис. 1.10) Складываемые векто- ры противоп � оложно направ-
Складываемые векто- ры противоп � оложно направ- a � � �
a � � �



 . (1.9)
. (1.9) Угол a между складываемыми векторами произвольный (рис. 1.13) (a не равен 0°, 90°, 180°, как это име- ло место выше). В этом случае при- меняется теорема косинусов: Квадрат одной стороны треугольника равен сум- ме квадратов двух других сторон ми- нус удвоенное произведение сторон на
Угол a между складываемыми векторами произвольный (рис. 1.13) (a не равен 0°, 90°, 180°, как это име- ло место выше). В этом случае при- меняется теорема косинусов: Квадрат одной стороны треугольника равен сум- ме квадратов двух других сторон ми- нус удвоенное произведение сторон на


