Геометрический смысл определенного интеграла

b

Интеграл ò f (x) dx численно равен площади, ограниченной частью графика функ a ции y = f (x), осью OX и ординатами f (a) и f (b), взятой со знаком «+» или «–», согласно схеме на рис. 3.3.

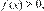Если кривая пересекает ось OX один или несколько раз внутри интервала [ а, b ], то интеграл численно равен алгебраической сумме площадей, находящихся по каждую сторону оси OX.

 

Рис. 3.3

 

ФИЗИЧЕСКИЙ СМЫСЛ ИНТЕГРАЛА

Интегральное исчисление возникло из потребности создать общий метод определения площадей, объемов и центров тяжести.

В зародышевой форме такой метод применялся еще Архимедом. Систематическое развитие он получил в XVII веке в работах Кавальери, Торричелли, Ферма, Паскаля и других ученых. В 1659 г. Барроу (учи- тель Ньютона) установил связь между задачей об определении площа- ди и задачей о касательной. Ньютон и Лейбниц в 70-х годах XVII века

 

перешли от частных геометрических задач к установлению связи ме- жду интегральным и дифференциальным исчислением.

Эта связь использована Ньютоном, Лейбницем и их учениками для развития техники интегрирования. Своего нынешнего состояния методы интегрирования достигли в работах Л. Эйлера, М. В. Остро- градского и П. Л. Чебышева.

Итак, интегрирование — операция, обратная дифференцирова- нию. Поэтому если физическая величина X является производной по времени или координате от другой величины Y

X = dY, (3.4)

dt

то, зная величину X, можно найти зависимость величины Y от вре- мени как интеграл.

Y = ò Xdt. (3.5)

Так как явления природы протекают в пространстве и во време-

ни, многие физические величины являются интегралами по времени

t или координате (x, y, z) от других величин. Приведем примеры.

Мощность P — это скорость совершения работы А

P = dA. (3.6)

Поэтому работа

dt

A = ò Pdt

 

(3.7)

Скорость � - это производная радиус-вектора � по времени t

v � r

� dr

Поэтому радиус-вектор

v =. (3.8)

dt

� �

r = ò vdt. (3.9)

Ток I — это скорость изменения заряда q

I = dq. (3.10)

Поэтому заряд

dt

q = ò Idt. (3.11)

Плотность тела r связана с массой m и объемом V как

r = dm. (3.12)

dV

Поэтому масса тела

m = òr dV. (3.13)

Линейная плотность заряда l определяется как

l = dQ. (3. 14)

dx

Поэтому заряд

Q = òl dx. (3.15)

ТАБЛИЦА НЕОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ

Для определения интеграла от элементарных функций пользуют- ся таблицей интегралов, приведенной ниже.

Таблица основных интегралов (постоянные интегрирования в таблице опущены)

ò n xn +1 x dx =;(n ¹-1) n +1	(1)	ò dx = tgx cos2 x	(9)
ò dx = ln x x	(2)	ò dx = - ctgx sin2 x	(10)
ò exdx = ex	(3)	dx 1 x ò a 2 + x 2 = a arctg a	(11)
ò x ax 0 dx = ln a	(4)	ò dx = 1 ln a + x; (для ⎪ x ⎪< a) a 2 - x 2 2 × a a - x	(12)
òsin xdx = -cos x	(5)	ò dx = 1 ln x - a; (для ⎪ x ⎪> a) x 2 - a 2 2 × a x + a	(13)
òcos xdx = sin x	(6)	ò dx = arcsin x a 2- x 2 a	(14)
ò tgx = - ln cos x	(7)	ò dx = ln x + x 2 + a 2 a 2 + x 2	(15)
ò ctgx = ln sin x	(8)	ò dx = ln x + x 2 - a 2 x 2 - a 2	(16)

Вопросы и задания для самопроверки

1. Дайте определение первообразной для данной функции.

2. Поясните геометрический смысл первообразной.

3. Поясните геометрический смысл определенного интеграла.

4. В чем отличия между неопределенным и определенным инте- гралом?

5. Поясните физический смысл определенного интеграла.

6. Пользуясь таблицей интегралов, найдите неопределенные ин- тегралы от следующих функций:

1) y = 9 x 2 - 2 x + 3,

2) y = 6 x 3 + 3 x - 4,

3) y = 5 x + 3sin x,

4) y = 7 x 3- 2 cos x,

5) y = x,

6) y = -sin x,

7) y = tg x,

8) y = 3 × cos2p x.

7. Приведите примеры физических величин, которые являются ин- тегралами по времени и координате от других физических величин.

 

Примеры решения задач

Задача 3.1

Скорость тела изменяется со временем по закону v (t) =, м/c.

Найти путь S, пройденный телом за время t = 10 с после начала дви- жения, и среднюю скорость v ср за это время.

Дано: v (t) = Найти: S (10), v ср.

, м/c; t = 10 c.

Так как путь S — это интеграл от скорости v (t) по времени t,

(S =ò v (t) dt), то S (t)=ò1+ tdt =

2 (1+ t)2 + C.

3

В полученную зависимость пройденного телом пути от времени S (t) подставим значения времени t 1 = 0 c и t 2 = 10 с (это будут ниж- ний и верхний пределы интегрирования) и определим путь S (10), пройденный телом за 10 с

 

 

S (10) =

2 (1+ t)2

= 2 (11

3

 

-1)» 23, 7 м.

По определению средней скорости

v (t) = S (t)

cp t.

Тогда средняя скорость тела за время t = 10 c

v (10) = S (10) = 23, 7» 2,37 м/с.

cp t 10

Ответ: путь, пройденный телом за первые 10 с после начала дви- жения, S (10)» 23,7 м; средняя скорость за этот промежуток време- ни v cp (t)» 2,37 м/с.

Задача 3.2

Какую работу A надо совершить, чтобы тело массой m поднять с поверхности Земли, радиус которой R, на высоту h? Найти работу при удалении тела на бесконечность.

Дано: m, R, h. Найти: Ah, A ¥.

Сила, действующая со стороны Земли на тело массой m, опреде-

ляется законом всемирного тяготения F = G mM, где r — расстоя-

r 2

ние от центра Земли до тела, G — гравитационная постоянная, M —

масса Земли. Если радиус Земли R, то работа, совершаемая для под- нятия массы m с поверхности Земли (r = R) до высоты h (r = R + h), вычисляется по формуле

R + h mM

⎛ 1 1 ⎞

Ah = ò G 2

r

R

dr = GmM ⎜⎝ R - R + h ⎟⎠.

На поверхности Земли (где r = R) сила, действующая на тело, F = mg (g — модуль вектора ускорения свободного падения), поэто- му GM = gR 2 и

A = mgR 2 ⎛1 -

 

1 ⎞ = mgh.

 

h ⎜⎝ R R + h ⎟⎠

1+ h

R

Для ответа на второй вопрос задачи найдем предел полученного выражения при h, стремящейся к бесконечности

 

 

lim A

= lim mgh = mgR, или A ¥= mgR.

h ®¥

h h ®¥ h

1

+

R

Ответ: чтобы тело массой m поднять с поверхности Земли радиуса R

на высоту h, необходимо совершить работу Ah

= mgh; чтобы удалить

1+ h

R

тело на бесконечность, необходимо совершить работу A ¥= mgR.

 

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

При решении физических задач часто возникают уравнения, на- зываемые дифференциальными. Такими являются уравнения дви- жения тел, составленные по второму закону Ньютона (если хотя бы одна из сил, действующих на тело, зависит от времени), уравнения незатухающих, затухающих и вынужденных колебаний, уравнения для расчета электрических цепей, составленные по правилам Кирх- гофа (если в цепи происходит переходный процесс).

Метод решения дифференциального уравнения определяется ви- дом уравнения; огромное число таких уравнений имеет только чис- ленное решение, в некоторых случаях решение дифференциально- го уравнения может подсказать сам характер исследуемого физиче- ского явления.

Рассмотрим виды дифференциальных уравнений, наиболее часто возникающих при описании физических процессов.