Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение моментов относительно оси. Закон сохранения момента импульса частицы
ОТНОСИТЕЛЬНО НЕПОДВИЖНОЙ ОСИ � Рассмотрим проекции момента импульса частицы L на ось z от- носительно двух произвольных точек О и О', лежащих на этой оси (рис. 4.4). Из (4.5) следует, что � � Lz = Lz ¢ + [ R, p ] z.
Lz = Lz ¢. (4.12) Аналогично можно показать, что Mz = M z ¢. (4.13)
Моментом импульса Lz ч � астицы относительно оси z называется про- екция на эту ось вектора L, определенного относительно произволь- ной точки О этой оси (рис. 4.5а) Lz = L cos a, (4.14) � где a – угол между вектором L и осью z. Момент импульса частицы относительно оси z одинаков для всех точек оси z (4.12). Моментом силы Mz, действующей на ча � стицу относительно оси z, называется проекция на эту ось вектора M, определенного относи- тельно произвольной точки О этой оси (рис. 4.5б). Mz = M cos b, (4.15) � где b — угол между вектором M и осью z. Момент силы, действующей на частицу относительно оси z, одинаков для всех точек оси z (4.13). Спроектируем на неподвижную ось z векторное уравнение (4.10). По- лучим
. (4.16) Уравнение (4.16) называется уравнением моментов относительно неподвижной оси. Из (4.16) следует закон сохранения момента импуль- са частицы относительно неподвижной оси: если Mz = 0, то Lz = const, (4.17) или
Lz (t1) = Lz(t2).
Рис. 4.5 Если алгебраическая сумма моментов сил, действующих на части- цу относительно некоторой неподвижной оси, равна нулю, то момент импульса частицы относительно этой оси остается постоянным.
Вопросы и задания для самопроверки 1. Дайте определение момента импульса частицы и момента силы относительно неподвижной точки О. 2. Дайте определение плеча силы. 3. В каких случаях момент силы равен нулю? 4. Может ли меньшая сила создать больший момент силы? 5. Почему канатоходцы держат в руках длинный тонкий шест? 6. Запишите уравнение моментов. 7. Сформулируйте закон сохранения момента импульса частицы. 8. Дайте определение момента импульса частицы и момента силы относительно оси. 9. Зависит ли момент импульса частицы и момент силы относи- тельно оси от выбора точки на этой оси? 10. Запишите уравнение моментов относительно оси. 11. Сформулируйте закон сохранения момента импульса части- цы относительно оси.
Задача 4.1 Найти момент импульса Луны мас- сой М Л относитель- но центра Земли массой М З и элек- трона массой me в Примеры решения задач
Луна
Электрон атоме водорода относительно протона, если они движутся по круго- вым орбитам радиусов R и r соответственно. Выразить через момент импульса L их кинетическую, потенциальную и полную энергии. Ме- няются ли со временем моменты импульса Луны и электрона? Дано: М Л, М З, me; R, r. � Найти:, Т, U, Е; L, Т, U, Е. L Л Л Л Л e е е е Движение Луны вокруг Земли Запишем второй закон Ньютона для Луны, двигающейся по ок- р�ужности радиуса R вокруг центра Земли. Так как единственной силой F, действующей на Луну, является сила ее гравитационного притяже-
ния к Земле (остальными пренебрегаем из-за их малости), то, следо- вательно, она является центростремительной силой, которая создает v 2
M a = G M З M Л , (1)
или
Л п R 2
M v 2 = G M З M Л Л R R 2 , (2) где G — гравитационная постоянная. Сокращая левую и правую час- ти уравнения на М Л и R, получаем
или v 2 = G M З
, (3)
По определению момент импульса Луны относительно центра Земли равен � � �
Вращая правый винт от первого вектора ко второму � по край- R p чайшему пут�и, по его поступате�льному движению определяем на-
. (5)
и, следовательно, v = L. (6) RM Л � � � � �
нии вокруг Земли. Кинетическая T и потенциальная U энергии дви- жения Луны вокруг Земли равны
R
. (8) Подставляя (6) в (7) и (5) в (8), получаем
2 2 M Л R 2
M R 2, 2 M Л R 2
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 666; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.152.99 (0.011 с.) |
 dLz = M dt z
dLz = M dt z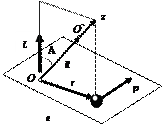



 центростремительное (нормальное) ускорение an = R и
центростремительное (нормальное) ускорение an = R и


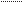 R
R v =. (4)
v =. (4) L = Rp sin p = RM v = RM = M
L = Rp sin p = RM v = RM = M 2 Л Л Л
2 Л Л Л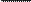 2, (7)
2, (7) U = - G M Л M З
U = - G M Л M З