
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Законы сохранения и изменения энергии
Замкнутая система Рассмотрим изолированную систему материальных тел m 1, m 2, m 3, …, между которыми действуют только силы тяготения или упругости (потенциальные силы). Запишем для каждого материального тела уравнение второго закона Ньютона. � � � �
⎧ m dv 1 = F + F +... + F, ⎪ 1 dt 12 13 1 n ⎪ � � � � ⎪⎪ m dv 2= F + F +... + F,
⎨ 2 dt ⎪.. 21 23 2 n (3.44) ⎪ � � � �
⎪ m dvn = F + F +... + F, � ⎪⎩ n dt n 1 n 2 n, n -1 где Fik – сила, действующая на i -ю точку со стороны k -ой (вн�утрен�няя с�ила). Отметим, что в уравнениях отсутствуют слагаемые F 11, F 22 …, Fii …, так как тела взаимодействуют только между собой и не взаимо- действуют сами с собой. В дальнейшем изложен�ии будем формально считать все эти слагаемые равными нулю, т. е. Fii = 0 (i = 1, 2,..., n).
� dx 1 � dx 2 ... � dxn Учитывая, что � �
умножим каждое уравнение системы (3.44) слева на � t, а справа на � dxi. В результате имеем
� � � vi d ⎧ m (�, �) - (F + F +... + F) d � = 0, ⎪ 1 v 1 dv 1 1�2 1�3 1� n x 1 ⎪ m (�, �) - (F + F +... + F) d � = 0, ⎨ 2 v 2 dv 2 21 23 2 n x 2 (3.45) ⎪... � � � � � � ⎪ m (v, dv) - (F + F +... + F) dx = 0. ⎩ n n n n 1 n 2 n, n -1 n Складывая все эти уравнения, получим n � � n � � � � å mi (vi, dvi) -å Fi 1+ Fi 2 +... + Fin) dxi = 0. (3.46) i =1 i =1 Данное соотношение можно переписать в более краткой форме n � � n � � å mi (vi, dvi) - å Fijdxi = 0. (3.47) i =1 i, j =1 Первое слагаемое в этом равенстве n � � n ⎛ m v 2 ⎞
(3.48) i =1 i =1 ⎝ 2 ⎠ представляет собой бесконечно малое изменение кинетической энер- гии всей системы. Второе слагаемое — бесконечно малая работа всех внутренних сил системы. Согласно рассмотрению п. 3.4 работа есть бесконечно малое уменьшение потенциальной энергии. Поэтому ее можно представить в виде n � � å Fij dxi = - dU. (3.49) i, j =1 С учетом введенных обозначений (3.48) и (3.49) равенство (3.47) перепишем в виде
или dK + dU = 0
dt Отсюда следует, что полная энергия системы, в которой действу- ют только внутренние силы, для любого момента времени остается величиной постоянной, т. е.
e = K + U = const. Значение const в последнем равенстве определяется значениями кинетической K 0 и потенциальной U 0 энергий системы в какой-то оп- ределенный момент времени e = K + U = K 0 + U 0. Полная энергия изолированной системы, в которой действуют толь- ко упругие силы или силы всемирного тяготения, есть величина посто- янная. Это закон сохранения энергии в механике, который для рас-
сматриваемого случая (отсутствуют силы трения) непосредственно вытекает из второго и третьего законов Ньютона.
Незамкнутая система Если система материальных тел не изолированная, то кроме внут- ренних сил, действующих между телами системы, на некоторые из них действуют внешние силы. Работу внешних сил нельзя учесть как из- менение потенциальной энергии системы, и закон сохранения энер- гии должен быть сформулирован в ином виде. Рассмотрим теперь систему материальных тел m 1, m 2, m 3,…, и для каждого из них запишем уравнение второго закона Ньютона ⎧ dv
⎪ m 1 1 = F 12 + F 13 +... + F 1 n + Ф 1, ⎪ dt ⎪ m dv =
+ +... + +, ⎪ ⎨ ⎪... 2 dt F 21 F 23 F 2 n Ф 2 ⎪ dv
⎪ mn n = Fn 1+ Fn 2 +... + Fn, n -1 + Фn. ⎩⎪ dt
— внешние силы, действующие на тела с массами m 1, m 2, m 3,… соответственно. В краткой форме систему можно переписать в виде dv n mi i = å Fij + Фi, i = 1, 2…, n (3.50)
dt j =1 � Умножая каждое уравнение системы (3.50) слева на vi dt, а спра-
m (v, dv) - å(, dx) = (, dx)
i i i
j =1 Fij i Фi i.
å i =1 n i i i, j =1 (, dx) = å n i =1 (, dx) . (3.51) Если дополнительно к обозначениям
n � � n ⎛ m v 2 ⎞ n � � å m (v, dv) = å d ⎜ ii ⎟= dK; å F dx = - dU i =1 i i i
i =1 ⎝ 2 ⎠
i, j =1 ij i
dA = å(, dx), i =1 то равенство (3.51) принимает вид dK + dU = dA или
d e = d (K + U) = dA. При конечных изменениях конфигурации системы изменение ее полной энергии Äe равно работе, совершенной всеми внешними си- лами Фi. При переходе системы из состояния 1 в какое-либо другое состояние 2, имеем
или Äe12 = ò d (K + U) = A 12.
Äe12 = e1 – e2 = A 12, (3.52) e1, e2 – полные энергии системы в начальном и конечном состояни- ях. Согласно (3.52), изменение полной энергии системы при переходе из одного состояния в другое равно работе, совершенной при этом внеш- ними силами. Данное утверждение — более общая формулировка за- кона сохранения энергии в механике. Если в замкнутой системе действуют силы трения, то их работа не может быть учтена изменением потенциальной энергии системы. По- этому работу сил трения необходимо учитывать как работу внешних сил. Силы трения направлены навстречу перемещениям тел, и рабо- та, совершаемая ими отрицательна, т. е. Äe12 = A 12 < 0, полная энергия e в замкнутой системе убывает. В замкнутой системе, в которой дей- ствуют силы трения, полная механическая энергия при движении не сохраняется. Следовательно, закон сохранения механической энер- гии несправедлив. Однако при таком «исчезновении» механической энергии всегда возникает эквивалентное количество энергии друго- го вида — тепловой энергии. Таким образом, когда «исчезает» энергия одного вида, всегда воз- никает эквивалентное количество энергии других видов. Это утвер-
ждение подтверждается многочисленными экспериментальными ис- следованиями и не имеет исключений. Закон сохранения энергии в его общем физическом смысле формулируется следующим образом: энергия никогда не исчезает и не появляется вновь, она лишь переходит из одной формы в другую. Закон сохранения механической энергии представляет собой след- ствие законов движения и не является самостоятельным законом. Всеобщее же значение закона сохранения энергии выступает именно там, где он не является следствием законов движения. Там, где закон сохранения механической энергии оказывается несправедливым, т. е. не выполняется, всегда можно указать другие виды энергии, в кото- рые превращается «исчезнувшая» механическая энергия. Согласно классической физике энергия любой системы меняет- ся непрерывно и может принимать любые значения. Квантовая тео- рия утверждает, что энергия микрочастиц, движение которых проис- ходит в ограниченном объеме пространства, может принимать толь- ко дискретный ряд значений.
Вопросы и задания для самопроверки 1. Дайте определение замкнутой и незамкнутой системы, потен- циального поля, консервативных (потенциальных) и непотенциаль- ных сил. Приведите примеры. 2. Почему приведенное выше рассмотрение ограничено лишь си- лами тяготения и упругими силами? 3. Запишите систему уравнений движения для замкнутой и не- замкнутой системы материальных тел. 4. Дайте определение полной механической энергии системы ма- териальных тел. 5. Выведите закон сохранения механической энергии для замкну- той и незамкнутой систем материальных тел. 6. Покажите, что в замкнутой системе тел увеличение их кинети- ческой энергии равно уменьшению потенциальной энергии. 7. Установите взаимосвязь между изменением полной энергии не- замкнутой системы тел с работой внешних сил, действующих на нее.
8. Почему силы трения, действующие в замкнутой системе, при- водят к нарушению закона сохранения механической энергии?
9. Почему закон сохранения механической энергии нельзя счи- тать самостоятельным законом? 10. Сформулируйте закон сохранения энергии в общефизическом смысле и обоснуйте ограниченность закона сохранения механиче- ской энергии.
Задача 3.10 Тело бросают вертикально вверх с начальной ско- ростью v 0 = 9 м/с. Найти высоту h, на которой его кинетическая энергия в n = 3 раза меньше потенци- альной. Дано: v 0 = 9 м/с; U (h)/ K (h) = n. Найти: h. Для решения задачи составим следующую систему уравнений:
K (h) U (h) = mgh mv 2
— потенциальная энергия тела на высоте h; (2)
– кинетическая энергия тела на высоте h; (3) mv 2 K (h) + U (h) = 0 — закон сохранения механической энергии. (4) В системе уравнений приняты обозначения: K (h), U (h) – кинети- ческая и потенциальная энергии тела на высоте h; m – его масса; v – скорость тела на высоте h. Неизвестными являются четыре парамет-
m m из этих неизвестных. Для этого равенство (4) представим в виде ⎛ K (h)⎞ mv 2 U (h) ⎜1+ ⎟= 0.
⎝ U (h) ⎠ 2 Последнее равенство с учетом соотношений (1) и (2) перепишем в виде ⎛ 1 ⎞
mv 2
⎟⎠ = 0.
Отсюда получим окончательный результат, представленный в от- вете. Ответ: h = n
v 2
2 g Задача 3.11 Тело бросают со скоростью v 0 = 12 м/с с высоты h = 30 м под уг- лом a = 24° к горизонту. Найти скорость v тела в момент падения на землю. Дано: v 0 = 12 м/с; h = 30 м; a = 24°. Найти: v. Используя закон сохранения энергии, имеем mv 2
mv 2 . (1) 2 2 Первое слагаемое в левой части уравнения (1) представляет собой потенциальную энергию тела на высоте h, второе — кинетическую энергию, связанную с его броском. При движении тела его потенци- альная и кинетическая энергии меняются так, что их сумма остается величиной постоянной и равной левой части уравнения (1). В момент падения потенциальная энергия тела становится равной нулю, а ки- нетическая энергия определяется значением скорости, которую не- обходимо найти по условию задачи (правая часть уравнения (1)). Из (1) найдем значение скорости v тела в момент падения на землю
Подставляя в последнюю формулу численные значения парамет- ров, получим величину скорости, представленную в ответе.
Ответ: v = = 27,1 м/с.
Задача 3.12 Тело массой m бросают с начальной скоростью v 0 под углом a к го- ризонту c высоты h над поверхностью земли. Используя кинематиче-
ские соотношения, найти зависимости кинетической K (t) и потен- циальной U (t) энергии тела от времени t и показать для него выпол- нение закона сохранения механической энергии, т. е. независимость от времени полной энергии тела e = K (t) + U (t) = const. Дано: m, v 0, a, h. Найти: K (t), U (t), e = K (t) + U (t) = const. Кинетическая энергия движущегося со скоростью v (t) тела, его потенциальная энергия на высоте y (t) и полная механическая энер- гия определяются соотношениями mv 2 (t) K (t) = ; U (t) = mg y (t); e = K (t) + U (t). (1)
Скорость тела в произвольный момент времени t
Проекции скорости тела, брошенного с начальной скоростью v 0 под углом a к горизонту, имеют вид vx = v 0 cosa, (3) vy (t) = v 0 sina – gt. (4) Подставляя их в соотношение (2), имеем v 2(t) = v 2- 2 v gt sin a + (gt)2. (5) 0 0
Учитывая, что v (t) = dy (t) получим зависимость высоты (y — ко- y dt, ординаты) тела от времени t y (t) = ò vy (t) d t = h + v 0 t sin a - Подставляя (5) и (6) в (1), имеем
gt 2
K (t) = m (v 2- 2 v gt sin a + (gt)2); (7)
2 0 0 gt 2 U (t) = mg (h + v 0 t sin a - ). (8)
Складывая кинетическую (7) и потенциальную (8) энергии, полу- чим полную механическую энергию тела mv 2 e = K (t) + U (t) = 0 + mgh, (9)
которая является постоянной, не зависящей от времени величиной. Однако каждое входящее в нее слагаемое от времени зависит. Со- отношение (9) представляет собой закон сохранения механической энергии. Ответ: e = const; K (t) = m (v 2 - 2 v gt sin a + (gt)2); U (t) = mg (h + v t sin a - gt).
2 0 0 0 2 Задача 3.13 Тело массой m совершает гармонические колебания с циклической частотой w и амплитудой А на невесомой пружине с коэффициентом упругости k. Найти зависимости кинетической K (t) энергии тела и потенциальной U (t) энергии пружины от времени t и показать выпол- нение закона сохранения механической энергии, т. е. независимость от времени полной энергии системы e = K (t) + U (t) = const. Дано: k; x (t) = A sin w t. Найти: K (t), U (t), e = K (t) + U (t) = const. Кинетическая энергия движущегося со скоростью v (t) тела, по- тенциальная (упругая) энергия и полная механическая энергия сис- темы (тело + пружина) определяются соотношениями K (t) = mv 2 (t)
kx 2 (t)
Зная зависимость координаты тела от времени (тело совершает гар- монические колебания с циклической частотой w и амплитудой А!) x (t) = A sin w t, (2) можно найти проекцию его скорости на ось, вдоль которой проис- ходит смещение тела vx = x' (t) = A w cosw t, (3) и скорость в произвольный момент времени t
mv 2 (t)
m w2 A 2 cos2 w t, (5) 2 2 kx 2 (t)
kA 2 sin2w t. (6) 2 2
Складывая кинетическую (5) и потенциальную (6) энергии, полу- чим полную механическую энергию тела и пружины
+ kA sin2w t. (7)
Из последнего соотношения довольно трудно заключить, что пол- ная механическая энергия не зависит от времени. Принимая во вни- мание зависимость периода колебаний тела от его массы и упругости пружины и взаимосвязь между периодом и циклической частотой
w получим
Подставляя последнюю формулу в первое слагаемое соотноше- ния (7), имеем
(sin2 w t + cos2 w t) = kA 2
2 2 Таким образом, полная механическая энергия системы, состоящей из тела и пружины, на которой оно колеблется, является сохраняю- щейся, не зависящей от времени величиной. Это обусловлено тем, что в системе действуют только потенциальные силы — сила тяже- сти и упругая сила. Ответ: e = const; mv 2 (t)
m w2 A 2 kx 2 (t)
kA 2 sin2 w t. 2 2 2 2
Найти начальную скорость v 0 тела, на- правленную вдоль плос- кости, составляющей угол a = 45° с горизон- том, его ускорение а и коэффициент μ трения тела о плоскость, если
при движении вверх до остановки оно проходит путь S = 3 м за вре- мя t 1 = 0,8 с. Дано: S = 3 м; t 1 = 0,8 с; a = 45°. Найти: v 0, а, μ. Для решения задачи составим следующую систему уравнений:
работы внешней силы; (1)
— энергия (кинетическая) тела в момент остановки; (4) A тр = F тр× S = F тр× S ×cos p — работа силы трения; (5) F тр + mg + N = ma — второй закон Ньютона; (6) F тр – mg sina = ma — проекция векторного уравнения (6) на ось Ох (см. рис); (7) – mg cosa + N = 0 — проекция уравнения (6) на ось Оy; (8) F тр = m N — сила трения тела о плоскость; (9) v (t) = v 0 – at — зависимость скорости движения тела от времени. (10) Из уравнений (8), (9) найдем значения силы реакции N = mg cosa и силы трения
F тр = m mg cosa. Подставим полученные значения сил реакции и трения в соотно- шения (7), (5) и (1) и перепишем систему уравнений (1–10) в виде
mgS sin a - 0 = -m mgS cosa — закон сохранения энергии; (11) a = g (sin a + m cos a ) — ускорение тела; (12) v 0 – at1 = 0 — скорость тела (13) в верхней точке движения на высоте h в момент времени t 1.
Из соотношения (11) имеем
С другой стороны, согласно (12),(13)
. (14) v 0 = at 1= gt 1(sin a + m cos a). (15) Из равенства (14) и (15) найдем коэффициент трения тела о по- верхность
- tga. (16) Подставляя (16) в (15) и (12), получим окончательные выражения для начальной скорости и ускорения тела
1 1 Примечание: задачу 3.14 можно решить, не используя закон сохра- нения энергии, рассматривая следующую систему уравнений:
⎪ at 2
В этой системе первые два уравнения кинематические, третье — динамическое (второй закон Ньютона). Решите систему самостоя- тельно и получите результаты, представленные в ответе.
=2 S t 1 = 7,5 м/с; a = 2 S
= 9,38 м/с2;
- tga = 0,35.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 444; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.200.66 (0.219 с.) |



 d (K + U) = 0.
d (K + U) = 0.




 Примеры решения задач
Примеры решения задач U (h) = n — условие задачи (1)
U (h) = n — условие задачи (1) K (h) =
K (h) =


 1+ n
1+ n mgh + 0 =
mgh + 0 = v =. (2)
v =. (2) Обратите внимание, что конечный результат (2), не зависит от угла бросания к горизонту. Это связано с тем, что работа силы тяже- сти при движении тела не зависит от формы его траектории, а опре- деляется только высотой, с которой брошено тело.
Обратите внимание, что конечный результат (2), не зависит от угла бросания к горизонту. Это связано с тем, что работа силы тяже- сти при движении тела не зависит от формы его траектории, а опре- деляется только высотой, с которой брошено тело. 2
2
 . (6)
. (6)
 2
2
 ; U (t) =
; U (t) = ; e = K (t) + U (t). (1)
; e = K (t) + U (t). (1)


 v = vx (t) = A w cosw t. (4) Подставляя (2) и (4) в (1), имеем
v = vx (t) = A w cosw t. (4) Подставляя (2) и (4) в (1), имеем
 K (t) = =
K (t) = =
 U (t) = =
U (t) = = K (t) U (t) cos2 t
K (t) U (t) cos2 t

 T = 2p; T = 2p,
T = 2p; T = 2p, w =.
w =. e= kA 2
e= kA 2 .
. K (t) = =
K (t) = =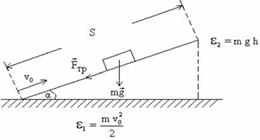 Задача 3.14
Задача 3.14 e2 – e1 = A тр — закон сохранения энергии с учетом
e2 – e1 = A тр — закон сохранения энергии с учетом mv 2
mv 2 v 0 =
v 0 = m = 2 S
m = 2 S

 1,
1,
 m = 2 S
m = 2 S


