
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Коэффициент внутреннего трения
Сила сопротивления среды При движении твердых тел в жидкости или газе, кроме силы внут- реннего трения, на тело (в случае больших скоростей и размеров тел) на- чинает оказывать существенное влияние сила сопротивления среды F сопр = r S u2 = bu2, (2.23)
Тело, движущееся в среде, испы- тывает действие двух сил: силы вязко- го трения (F тр) и силы сопротивления (F сопр). При небольших скоростях сила сопротивления меньше силы вязкого трения, а при больших — значительно превосходит ее (рис. 2.8). При некотором значении скорости u¢ силы F тр и F сопр становятся равными по модулю. Сила сопротивления среды зависит от формы движущегося тела. Форму Рис. 2.8 тела, при которой сила сопротивления мала, называют обтекаемой. Ракетам, самолетам, автомобилям и другим машинам, движущимся с большими скоростями в воздухе или в воде, придают обтекаемую, каплеобразную форму.
Сила упругости
Рис. 2.9 Различают деформацию упругую Х и неупругую. При упругой деформа- ции тело после прекращения дейст- вия внешних сил полностью восста- навливает свою форму и размеры. При неупругой деформации фор- ма и размеры тела не восстанавли- ваются. Остановимся подробно на упру- гой деформации. При растяжении пружины на ве- личину x (рис. 2.9) относительно ее равновесного положения возни-
упр , которая возвращает пружину в прежнее со- стояние после прекращения действия внешней силы (х 0 = 0). В соот- ветствии с законом Гука: упругая сила Fx, возникающая при линейном растяжении или сжатии пружины, пропорциональна величине ее де- формации Fx = – k Ä x, (2.24) где Ä x = x – x 0 — деформация пружины; Fx — проекция силы упруго- сти на направление перемещения пружины; k — коэффициент упру- гости пружины, знак минус указывает, что направления силы и пере- мещения противоположны.
l 0
Рис. 2.10.
Однородные стержни ведут себя при растяжении или односторон- нем сжатии подобно пружине. Если к конца�м сте�ржня (рис. 2.10) при- ложить направленные вдоль его оси силы F 1 и F 2 (F 1 = F 2 = F s), дей- ствие которых равномерно распределено по всему сечению, то длина стержня l 0 получит положительную (при растяжении), либо отрица- тельную (при сжатии) деформацию Ä l. Деформацию стержня можно характеризовать относительным удлинением
e = Ä l. (2.25) l 0 Опыт показывает, что для стержня при упругой деформации от- носительное удлинение пропорционально силе F s, действующей на площадь его поперечного сечения S
S
ня, измеряемое в паскалях (Па = Н/м2). S Из-за взаимодействия частей стержня друг с другом напряжение передаётся во все его точки. Если внешние силы направлены по нор- мали к поверхности, напряжение называют нормальным, а по каса- тельной — тангенциальным. Нормальное напряжение F s/ s = s, тан- генциальное — F t/ s = t. Наряду с коэффициентом упругости a для характеристики упругих свойств тел при нормальных напряжениях используют модуль Юнга Е = 1/a, который, как и напряжение, измеряется в паскалях. Относительное удлинение (сжатие) и модуль Юнга в соответствии с равенствами (2.25 и 2.26) определяется из соотношений e = s, E = s l 0.
E Ä l Модуль Юнга равен такому нормальному напряжению, при ко- тором деформация стержня Ä l равна его первоначальной длине l 0. В действительности при таких напряжениях происходит разруше- ние стержня. Решая уравнение (2.26) относительно F s, и подставляя вместо e = Ä l / l 0, a = 1/ Е, получим формулу для определения силы дефор- мирующей стержень с сечение S на величину Ä l
l 0 F = ES Ä l, (2.27)
— постоянный для стержня коэффициент, который в соответ- ствии с законом Гука соответствует коэффициенту упругости стерж- ня при его сжатии и растяжении.
b раллелепипеда высотой b, и приложим к его проти-
F 1 и F 2 (F 1 = F 2 = F t), на- Рис. 2.11 правленные параллельно граням (рис. 2.11).
Если действие сил равномерно распределено по всей поверхно- сти соответствующей грани тела, то в любом сечении, параллельном этим граням, возникает тангенциальное напряжение
S где S — площадь грани. Под действием напряжений тело деформи- руется так, что одна грань сместится относительно другой на неко- торое расстояние а. Если тело мысленно разбить на элементарные, параллельные рассматриваемым граням слои, то каждый слой ока- жется сдвинутым относительно соседнего с ним слоя. При деформации сдвига любая прямая, первоначально перпен- дикулярная к слоям, повернется на некоторый угол j. Деформация сдвига характеризуется отношением
b которое называется относительным сдвигом. При упругих деформа- циях угол j — очень мал, поэтому можно положить tgj» j и g = j. Опыт показывает, что относительный сдвиг пропорционален тан- генциальному напряжению
g = 1 t = 1× F t,
G G × S где G — модуль сдвига, GS — постоянная величина для деформируе- мого тела. Модуль сдвига G = t g зависит только от свойств материа- ла и равен тангенциальному напряжению при угле j = 45°. Модуль сдвига так же, как и модуль Юнга измеряется в паскалях (Па). Сила, вызывающая сдвиг стержня сечением S на угол j, соглас- но (2.28), равна F t= G × S × g = G S j, (2.28) где G · S — коэффициент упругости стержня при деформации сдвига. Вопросы и задания для самопроверки 1. Дайте определение силы и перечислите ее разновидности в ме- ханике. 2. Определите порядок силы гравитационного взаимодействия ме- жду космическими телами (Земля и Луна) и силы между двумя вагона- ми с массами 50 т, находящимися на расстояние 10 см друг от друга. 3. Верно ли утверждение, что сила тяжести тела всегда равна его силе гравитационного притяжения к Земле? 4. Какие силы действует на тело, лежащее на горизонтальной опоре? 5. Будут ли одинаковыми показания весов, если тело взвешива- ют в вагоне, движущемся с постоянной скоростью и с постоянным ускорением? 6. Назовите силы, которые возникают при внешнем и внутрен- нем трении. 7. Запишите закон Гука для упругой деформации сжатия, растя- жения.
Примеры решения задач Задача 2.1. Тело массой m = 2 кгдвижется так, что зависимость координаты х от времени задаётся уравнением x = A cosw t, где A = 5 м, w = p рад/с. Определить максимальную силу F max и силу F (t), действующую в мо- мент времени t = 3 c.
Дано: x = A cosw t; m = 2 кг; A = 5 м; w = p рад/с; t = 3 c. Найти: F (t), F max. Тело движется в направлении оси Х под действием силы Fx = max, где ускорение
Тогда сила
d 2 x
x dt 2
F (t) = - mA w2 cosw t,
Ответ: F max F max = mA w2 = 98, 6 H, = mA w2.
F (t = 3 c) = - mA w2 cosw t = -98, 6 H.
Задача 2.2. Поезд движется прямолинейно и равномерно при действии на него сил сопротивления воздуха F сопр и трения о рельсы F тр. Опреде- лить равнодействующую сил F р, препятствующих движению, если сила тяги локомотива F тяг = 650 кН. Дано: F тяг = 650 кН. Найти: F р. При равномерном прямолинейном движе- нии равнодействующая всех сил
F сопр.
F тр. mg F тяги x
Сумма проекции сил на направление движения поезда Х F т – F тр – F сопр = 0, (1) F т = F тр + F сопр. Равнодействующая сил сопротивления движению поезда.
F р = F тр + F сопр = F т = 650 кН. Ответ: F р = F т = 650 кН.
Задача 2.3. Три груза с m 1 = 500 г, m 2 = 700 г и m 3 = 300 г связаны невесомой нитью и лежат на гладкой горизонтальной поверхности. К первому грузу приложена горизонтально направленная сила F = 6Н. Пренеб- регая трением, определить ускорение а и силу натяжения нити F 23 ме-
m 3 g m 2 g m 1 g Дано: m 1 = 500 г = 0,5 кг; m 2 = 700 г = 0,7 кг; m 3 = 300 г = 0,3 кг; F = 6Н. Найти: a, F 23. Урав�нен�ие дв�ижен�ия г�рузов� � � � � � F + F 12 + F 21 + F 23 + F 32 + N 1 + N 2 + N 3 + m 1 g + m 2 g + m 3 g =
Уравнение движения грузов в направлении Х F - F 12+ F 21- F 23+ F 32=(m 1+ m 2+ m 3)× a. (2) Так как нити невесомы и грузы относительно друг друга покоят- ся, то F 21 = F 12, F 32 = F 23. Грузы движутся с ускорением
m 1 + m 2 + m 3 Определим силу F 23 из систем уравнений:
F 12 F 1 a. X: ⎧- F 23 + F 21 = m 2 a, ⎨- F + F = m a. ⎩ 12 1
Учитывая, что F 12 = F 21, F 23 = F 21 - m 2 a F 12 = F - m 1 a. Тогда F 23= F - m 1 a - m 2 a = F - a (m 1+ m 2) =
m 1 + m 2 m 1 + m 2 + m 3 ) = F m 3.
Ответ: a = F
= 4 м/с2, F 23 = F m 3
= 1, 2 H. Задача 2.4 1 2 3 1 2 3
Тело массой m = 1 т движется с постоян-
X
N 2
F тр.2 X ной скоростью по горизонтальной плоскости с коэффициентом трения m = 0,2 в одном слу- чае под действием силы F 1, а в другом — силы F 2. Определить модули сил F 1 и F 2, если эти силы приложены к одной точке тела под уг- лом a = 45° к горизонту. Дано: a = 45°; m = 0,2; m = 1 т = 103 кг. Найти: F 1, F 2 Запишем системы уравнений движения груза для первого и второго случаев. F 2 mg ⎧� � � � ⎪ F тр1 + mg + N 1 + F 1 = 0, ⎨ � � � � ⎪⎩ F тр2+ mg + N 2+ F 2= 0, X: ⎧⎪- F тр1+ F 1cos a=0, Y: ⎧- mg + N 1 + F 1 sin a=0,
(1) ⎨- F + F cos a = 0 ⎨- mg + N - F sin a = 0. ⎩⎪ тр 2 2 ⎩ 2 2 Решим систему уравнений (1) относительно сил N 1, N 2 и F 1, F 2 N 1 = mg - F 1 sin a, N 2 = mg + F 2 sin a F = m mg, F = m mg. 1 (1+ m tg a) cosa 2 (1- m tg a) cosa
Ответ: F = m mg = 2,3 кН, F = m mg = 3,5 кН. 1 (1+ m tg a) cosa 2 (1- m tg a) cosa
Локомотив трогает с места состав вагонов с общей мас- сой m = 1600 т, при силе тяги F тяги = 400 кН. Определить N расстояние s, пройденное составом за время t = 5 мин, если коэффициент трения μ = 0,005.
F тр
g F тяг
X S Дано: u0 = 0; m =1600 т = 1,6 · 106 кг; μ = 0,005; F тяги = 400 кН = = 4 · 105 Н; t = 5 мин = 300 с. Найти: s.
Уравнение движения состава поезда � � � � � F тр + mg + N + F тяги = ma, (1) � �
где F тр,, N, — силы трения, тяжести и реакции рельс. Уравнения в проекциях сил на оси X и Y X: - F тр + F тяги = ma, Из решения уравнений (2) Y: - mg + N = 0, (2)
где F тр = m N = m mg. Тогда F - F
m N = mg,
m m Пройденный составом путь at 2 ⎛ F
⎞ t 2
s = = ⎜⎝ тяг - m g ⎟⎠. 2 m 2 ⎛ F ⎞ t 2
Ответ: s = ⎜⎝ - m g ⎟⎠ = 9000 м. m 2
Задача 2.6 Локомотив тянет состав из n = 4 одинаковых вагонов, массой m = 10 т с ускорением а = 10м/с2. Определить силу натяжения F 34 сцепки между третьим и четвертым вагоном, если коэффициент тре- ния колес вагона о рельсы равен m = 0,005.
Дано: m =10 т =104 кг; а = 10 м/с2; m = 0,005 = 5 · 10–3. Найти: F 34. Силы, действующие между вагонами F 12= F 21, F 23 = F 32, F 34 = F 43, (1) Уравнения движения для трех вагонов, начиная с первого в на- правлении оси Х:
(2)
F 34 = F 32 – F тр – ma = F тяг – 3 (F тр + ma), (3) где F тр = m mg — сила трения при движении одного вагона.
Силу тяги найдем из уравнения движения четырех вагонов с мас- сой 4 m движущихся с ускорением а под действием силы F тяг при силе трения Fтр = 4m mg F тяг — 4m mg = 4 ma, F тяг = 4 m (m g + а). Подставим соотношение для силы тяги в формулу (3).
F 34 = m (m g + a). Ответ: F тяг = 4 m (m g + а) = 4 · 105 Н, F 34 = m (m g + a) =105 Н.
Задача 2.7 Поезд движется со скоростью u1 = 72 км/ч, совпадающей с на- правлением скорости ветра u2 = 10 м/с. Во сколько раз увеличится сила сопротивления движению поезда F сопр = bu2, если он будет дви- гаться навстречу ветру с той же скоростью. Дано: u1 = 72 км/ч =20 м/с; u2 = 10 м/с. Найти: Сила сопротивления поезда пропорциональна квадрату его отно- сительной скорости u, которая в первом случае u = u1 – u2, во вто- ром — u = u1 + u2. Тогда отношение сил сопротивления
Ответ:
Задача 2.8 Грузовой автомобиль
F вой автомобиль массой m = 2 т с помощью троса с коэффициентом жест- кости k =100 кН/м. F тр F упр υ
g Найти удлинение Ä l троса, если автомобили движутся с коэффи- циентом трения колес μ = 0,2: а) с постоянной скоростью u, б) с ускорением a = 0,5 м/с2. Дано: m = 2 т = 2 · 103 кг; k =100 кН/м; a = 0,5 м/с2; μ = 0,2. Найти: Ä l 1, Ä l 2. Модуль силы натяжения упругости � F, деформирующей трос, равен силе
F упр. = k Ä l = F.
где F тр = m N = m mg. Из уравнения (1) .
Ä l 1 = m (a + m g ). k Уравнения движения автомобиля с постоянной скоростью � � �
Х: F тр + F = 0, -m mg + k Ä l 2 = 0, Ä l 2 = m mg. k Ответ: F тр = m (a +m g ) = 4,9 см, Ä l k 2 = m mg = 3,9 см. k
X
X
Автомобиль массой m = 1 т дви- жется со скоростью u = 54 км/ч, в од- ном случае по горизонтальной дороге, а в другом по профилированной с уг- лом наклона к горизонту a =15°. Оп- ределить минимальные коэффици- енты трения колес автомобиля с до- рогой, если он будет делать поворот по траектории с радиусом кривизны
б) R = 50 м без заноса. Дано: m = 1 т = 103 кг; R = 50 м; u = 54 км/ч = 15 м/с; a =15°. Найти: μ1, μ2.
Уравнение движения автомобиля
  Для горизонтальной дороги вдоль выбранных осей Для горизонтальной дороги вдоль выбранных осей
(2)
   для профилированной дороги для профилированной дороги
(3)
Решая системы уравнений (2) и (3) относительно μ1 и μ2, прини- u2 u2
u2 cos a - gR sin a
u2 u2cos a - gR sin a
Задача 2.10
начальная скорость u0 равна нулю. Дано: R = 5 м; u0 = 0. Найти: u.
n � d u t: m dt = mg sin a, � u2
R = mg cos a - N. (1)
Учитывая, что ds = u dt = Rd a, первое уравнение системы (1) за- пишем в виде u d u = gR sin a × d a. (2) Проинтегрируем левую и правую часть уравнения (2) в пределах изменения скорости от 0 до u и угла от 0 до a: u a òu d u = gR òsin a × d a, 0 0 u2 = 2 gR (1- cosa).
(3) Из второго уравнения системы (1) и уравнения (3), учитывая, что в момент отрыва тела от поверхности сферы N = 0, найдем его ско- рость
gR
 u2= - u2= -
2 gR (1
), (4) gR (5)
Задача 2.11 Тело массой m = 2 кг движется в направлении оси Х под дейст- вием силы Fx = F 0 sin w t. В момент времени t = 0 координата тела и его скорость равны нулю.�Определить зависимость от времени коор- динаты x (t) и скорости u(t) и их модули в момент времени t = 2 с, если w = 3,14 рад/с. Дано: Fx = F 0 sin w t; x 0 = 0; u x (0) = 0; t = 2 с; w = 3,14 рад/с; F 0= 5 H. Найти: x (t = 2 с); u(t = 2 с). Запишем уравнение движения тела вдоль направления оси Х:
Тогда dt m d u x = F 0 sin w × tdt. (2)
Проинтегрируем левую и правую часть последнего уравнения в пределах изменения скорости u и времени t u F t
0 m 0 (3) u x (t) = F 0 (1- cosw t).
Зависимость x (t) найдем интегрированием равенства dx (t) = u x (t) dt x F dx (t) = 0 t (1- cosw t) dt,
(4) x (t) = F 0
(w × t - sin w t). Ответ: x (t = 2 c) = F 0
(w × t - sin w t) = 1, 59 м, u x (t = 2 c) = F 0 (1- cos w t) = 0 м/с.
Задача 2.12 Путь, пройденный телом массой m = 2 кг, задается уравнением s = A + Bt + Ct 2 + Dt 3, где С = 0,1 м/с2, D = 0,03 м/с3. Определить за- висимость силы от времени F (t) и силу действующую на тело в мо- мент времени t = 0 и t = 10 с после начала движения. Дано: s = A + Bt + Ct 2 + Dt 3; С = 0,1 м/с2; D = 0,03 м/с3; m = 2 кг; t = 10 c Найти: F (t), F (0), F (10). Из основного уравнения динамики
где
d 2 s
Тогда m 2 = F (t), (1) F (t) = m (2 C + 6 Dt).
F (t = 0) = m × 2 C, F (t = 10) = 2 m (C + 3 Dt). Ответ: F (t = 0) = m × 2 C = 0, 4 Н, F (t = 10) = 2 m (C + 3 Dt) = 4 Н.
ОСНОВНЫЕ ПОЛОЖЕНИЯ · Свободное тело — тело, на которое не действуют какие-либо дру- гие тела. · Инерциальная система отсчета — система отсчета, в которой сво- бодное тело покоится или движется прямолинейно и равномер- но. · Неинерциальная система отсчета — система отсчета, в которой сво- бодное тело движется с ускорением. · Инертность — свойство тела сохранять состояние покоя или рав- номерное прямолинейное движение. · Масса — положительная скалярная величина, являющаяся мерой инертности тела, — не зависит от его скорости движения, — равна сумме масс всех частиц, из которых оно состоит. · Сила — векторная величина, являющаяся мерой механического взаимодействия тел. · Гравитационная сила — сила взаимного притяжения между двумя материальными точками (м. т).
g r 2 где G = 6, 6710-11 (Н · м2)/кг гравитационная постоянная, m 1, m 2 — массы взаимодействующих тел, r — расстояние между м. т или цен- трами масс тел�. · Сила реакции N — сила, действующая на тело со стороны опоры, или подвеса, препятствующая его движению. · Сила тяжести F тяж = mg — составляющая силы, гравитационного взаимодействия тела с Землeй. Основные положения 137
· Вес тела — сила, приложенная к горизонтальной опоре или подве- су, которые удерживают тело от свободного падения. При непод- вижной опоре (подвесе) или при их равномерном движении вес тела равен силе тяжести. · Третий закон Ньютона — силы взаимодействия двух материальных точек в инерциальной системе отсчета равны по модулю и проти- воположны по направлению � � F = - F, 1,2 � 2,1 гд�е F 1,2– сила, действующая на первую точку со стороны второй, F 2,1 – сила, действующая на вторую точку со стороны первой. · Сила упругости F упр = - k (l - l 0) = - k Ä l, где k — коэффициент упругости тела l 0, l - начальная и конечная его длина. · Сила трения возникает при взаимодействии соприкасающихся по- верхностей твердых тел или слоями жидкости или газа. · Сила трения покоя действует между неподвижными поверхностя- ми взаимодействующих тел и изменяется от нуля до максималь- ного значения F тр.max = m0 N, где m0 - коэффициент трения покоя, N — сила реакции опоры. · Сила трения скольжения F тр = m N — возникает при относительном движении соприкасающихся тел, где m — коэффициент трения скольжения. · Сила сопротивления F сопр» bu n, где b — коэффициент сопротивления, n — показатель степени за- висящий от величины скорости. · p = m u — векторная величина, характеризующая движение тела. • Первый закон Ньютона — материальная точка в инерциальной сис- теме отсчета сохраняет состояние покоя или равномерного прямо- линейного движения, если на нее не действуют силы или их дей- ствие скомпенсировано.
· Втор�ой закон Ньютона � F
m � — ускорение a, материальной точкой в инерциальной системе от- счета прямопропорционально действующей на точку силе, обрат- но пропорционально массе и совпадает по направлению с силой. · Уравнение движения — второй закон Ньютона, записанный в фор- ме дифференциального уравнения второго порядка
dt 2
ме отсчета.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 479; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.202.45 (0.373 с.) |
 где u — скорость движения тела; r — плотность среды (жидкости или газа); S — площадь поперечного сечения тела, b = r S — коэффици- ент сопротивления.
где u — скорость движения тела; r — плотность среды (жидкости или газа); S — площадь поперечного сечения тела, b = r S — коэффици- ент сопротивления. При действии на тело внешних сил возникает деформация и упру- гая сила F упр
При действии на тело внешних сил возникает деформация и упру- гая сила F упр

 e = a F s, (2.26)
e = a F s, (2.26) где a — коэффициент упругости стержня, F s — напряжение стерж-
где a — коэффициент упругости стержня, F s — напряжение стерж-


 Рассмотрим деформа- F 1 цию сдвига. Возьмём од-нородное тело, имеющее форму прямоугольного па-
Рассмотрим деформа- F 1 цию сдвига. Возьмём од-нородное тело, имеющее форму прямоугольного па- F 2 в�олеж�ащим граням силы
F 2 в�олеж�ащим граням силы t = F t,
t = F t, g = a = tgj,
g = a = tgj,



 N
N жду вторым и третьим грузом.
жду вторым и третьим грузом. a = F.
a = F. = F (1-
= F (1- m + m + m
m + m + m m + m + m
m + m + m Y
Y Y
Y
 a = тяг тр,
a = тяг тр,
 a = F тяг -m mg = F тяг - m g.
a = F тяг -m mg = F тяг - m g.



 mg mg mg mg
mg mg mg mg
 В результате решения уравнений (1) и (2) получим
В результате решения уравнений (1) и (2) получим
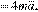
 .
. ,
, где b — коэффициент сопротивления воздуха движению поезда.
где b — коэффициент сопротивления воздуха движению поезда.

 �
� Х: –m mg + k Ä l 1 = ma, (1)
Х: –m mg + k Ä l 1 = ma, (1) + m g + N + F =0,
+ m g + N + F =0, Задача 2.9
Задача 2.9 Y
Y
 . (1)
. (1)





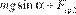





 профилированной m2 = u2 sin a+ gR cosa.
профилированной m2 = u2 sin a+ gR cosa. Ответ: m1 = Rg = 0,46, m2 = u2 sin a+ gR cosa= 0,17.
Ответ: m1 = Rg = 0,46, m2 = u2 sin a+ gR cosa= 0,17. Тело соскальзывает с вершины гладкой сферы радиуса R = 5 м. Оп- ределить скорость u тела в момент от- рыва от поверхности сферы, если его
Тело соскальзывает с вершины гладкой сферы радиуса R = 5 м. Оп- ределить скорость u тела в момент от- рыва от поверхности сферы, если его n: m
n: m u2= gR cos a, cos a =,
u2= gR cos a, cos a =,
 Ответ: u= = 5, 72 м/с.
Ответ: u= = 5, 72 м/с.
 d u x = F 0 sin w t. (1)
d u x = F 0 sin w t. (1) m
m m w
m w
 m w2
m w2 m w2
m w2
 F = G m 1 m 2,
F = G m 1 m 2,
 a =,
a =, m d r = F,
m d r = F,


