
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Мультиатрибутивная модель идеальной точкиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В то время как модель М. Фишбейна была разработана для понимания всевоз-можных типов установок, модель идеальной точки разработана специально для определения установок потребителей по отношению к товарам/* Формула, на которой основан метод идеальной точки, выглядит следующим образом:
где.
В данном случае потребителей просят указать, как, по их мнению, определенный товар располагается на шкале со значениями важных для них атрибутов. На тех же шкалах потребители должны разместить «идеальный» товар. Согласно нашей мо-дели, чем ближе фактические показатели товара к идеальным, тем благоприятнее установки по отношению к нему со стороны потребителей.
В качестве иллюстрации модели идеальной точки рассмотрим следующий при-мер. Предположим, что в качестве значимых атрибутов безалкогольных напит-ков были определены:
• сладость;
• степень газированности;
• калорийность;
• содержание натуральных фруктовых соков;
• цена.
Далее для каждого атрибута разрабатывается соответствующая шкала. Напри-мер, для первого атрибута — сладости — она будет выглядеть так:
После этого проводится опрос потребителей, в котором они указывают свой идеальный или предпочтительный вкус, поставив в одно из положений на шкале букву «/» (/г в нашей модели). Затем по этому же показателю оценивают различ-ные марки напитков (т. е. мы получаем значения Xt). Кроме того, потребители должны указать, насколько важным для них является данный атрибут. Для этого может использоваться такая шкала:
Абсолютно Очень неважен важен
Таблица 10.14. Гипотетические результаты применения мультиатрибутивноймодели установок идеальной точки
Предположим, что в ходе опроса мы получили результаты, представленные в табл. 10.4. В первом столбце указаны атрибуты, по которым оцениваются иде-альная (третий столбец) и реальные (четвертый и пятый столбцы) марки. Во вто-ром столбце приведены данные о значимости каждого атрибута.
В нашем примере наиболее важной характеристикой является вкус, а наиме-нее важной — газированность. По данным об идеальных точках можно сказать, что «идеальный» напиток должен быть сладким на вкус, слабо газированным, с небольшим числом калорий, высоким содержанием фруктовых соков (на прак-тике, возможно, для оценки содержания сока стоило бы использовать шкалу со 478Часть 3. Индивидуальные детерминанты поведения потребителей
значениями от 0 до 100%). Цена такого напитка должна быть относительно невысо-кой (здесь также можно использовать другую шкалу, например содержащую кон-кретные значения цен). Потребители считают, что марка «А» очень близка к иде-альной. Марка «Б» имеет высокие оценки по некоторым атрибутам (например по калорийности), но по другим (скажем, по газированности) явно проигрывает.
Итоговое значение установок относительно товара определяется следующим образом. Сначала мы находим разность между идеальным и фактическим значени-ем оценки атрибута. По вкусу у марки «А» эта разность равна нулю (2-2), а у марки «Б» она составляет -1 (2-3). Мы берем абсолютную величину разности (на что указывает символ модуля в формуле) и умножаем ее на значение важности. По ат-рибуту «вкус» мы получим для марки «А» — 0 (0 х 6), для марки «Б» — 6(1x6). Далее аналогичным образом определяются слагаемые по остальным атрибутам и, наконец, их сумма. Для марки «А» она равняется 16, для марки «Б» — 29. В отличие от модели М. Фишбейна, в которой чем больше значение, тем лучше, в данном слу-чае предпочтение отдается наименьшим результатам. Наилучшее значение устано-вок, которое может иметь марка, равно нулю, что говорит о том, что товар в точно-сти соответствует представлениям потребителей об идеальном наборе атрибутов.
|
|||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1068; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.170.67 (0.008 с.) |

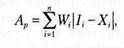

 — установки относительно товара;
— установки относительно товара;  — значимость показателя i; — «иде-альное» значение атрибута i;
— значимость показателя i; — «иде-альное» значение атрибута i;  — представление о фактической величине атрибу- та г; п — число значимых атрибутов.
— представление о фактической величине атрибу- та г; п — число значимых атрибутов.




