Однородность производственной функции

То, что представляется изменением вокруг нас, — лишь скорость судна, покидающего этот мир.

Джалал ad-дин Руми (1207-1273)

Зависимость прироста выпуска продукции от увеличения всех производствен­ных факторов является одной из важных характеристик производственного про-

¹ I о" о С, («равный» — греч.); clinamen («отклонение» — лат.).

Глава 5. Фирма и теория производства

К

Изоклиналь: MRTS = w/r

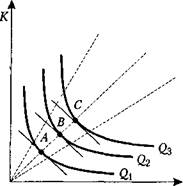
О I "

Рис. 5.13. Линия роста фирмы (изоклиналь)

цесса фирмы в долгосрочном периоде. При рассмотрении производственной функ­ции часто исходят из того, что при увеличении объема применяемых факторов про­изводства пропорционально возрастает и объем производства. Однако на практике это бывает далеко не всегда.

Часто (но не обязательно всегда) при увеличении масштабов относительно мелкого производства выпуск растет опережающими темпами по сравнению с увеличением факторов производства. В таком случае говорят, что имеет место возрастающая отдача от масштаба.

Затем, по мере дальнейшего роста объемов производства, отдача от масштаба может равняться приросту факторов производства. Это случай постоянной отда­чи от масштаба.

Наконец, достигнув какого-то уровня, отдача от масштаба замедляется по сравнению с увеличением объемов применяемых факторов производства. Это — убывающая отдача от масштаба.

Для оценки отдачи от масштаба используют понятие однородности. Произ­водственная функция называется однородной, если при увеличении всех факто­ров производства в k раз объем выпуска увеличивается в k раз. Здесь t — показатель степени однородности. Таким образом, производственная функция Q = Q(L, К) является однородной в степени t, если:

*Q-Q(kL,kK).

(5.19)

Если t= 1, то функция однородна в первой степени, а производство демонст­рирует постоянную отдачу от масштаба. В этом случае говорят, что производ­ственная функция линейно-однородная.

Если t> 1, то имеет место возрастающая отдача от масштаба.

Если t < 1 — налицо убывающая отдача от масштаба.

Поясним понятие отдачи от масштаба с помощью графика (рис. 5.14).

Когда производственный процесс фирмы характеризуется возрастающей от­дачей от масштаба (отрезок ОА луча), изокванты становятся ближе друг к другу. Это означает, что при пропорциональном увеличении труда (5, 10, 15 и т.д.) и капитала (1, 2,3 и т. д.) объем производства возрастает ускоряющимися темпами.

Часть I. Основы рыночного анализа

О L

Рис. 5.14. Отдача от масштаба

При убывающей отдачи от масштаба (отрезок АВ луча), напротив, изокванты располагаются все дальше друг от друга, так как требуется все большее и большее количество факторов производства для увеличения объемов производства.

О L

Рис. 5.15. Изокванты однородной производственной функции

При постоянной отдаче от масштаба (рис. 5.15) изокванты располагаются рав­номерно.

Отдача от масштаба существенно различается для разных фирм и отраслей. При прочих равных условиях, чем больше отдача от масштаба, тем более крупные фир­мы действуют в данной отрасли. Обычно производственные отрасли характеризу­ются большей отдачей от масштаба, чем сферы услуг, так как в материальном про­изводстве требуются существенные капиталовложения в оборудование.

Вернемся к производственной функции Кобба-Дугласа (Q = Л£^аА*). Ее сте­пень однородности равна (а + Ь). Особым случаем является функция Q = D^/2K^[/2, когда однородность функции Кобба-Дугласа линейна, т. е. демонстрирует посто­янную отдачу от масштаба.

Однородная производственная функция обладает следующими свойствами. Во-первых, отношение предельных продуктов (MP_K/MP_L = MRTS) не меняется,

Глава 5. Фирма и теория производства

если затраты (К и L) изменяются пропорционально. Это значит, что в каждой точ­ке любого луча, исходящего из начала координат на рис. 5.15 (т. е. в точках А, В, С и т. д.), наклон изоквант (Q,, Q_r Q₃ и т. д.) постоянен.

Во-вторых, в соответствии с теоремой Эйлера сумма частичных производных относительно независимой переменной равна произведению зависимой перемен­ной на степень однородности.

Теорема Эйлера: если выражение Y = (X_v Х₂, ■■,Х_п) однородно, то ^^ЭУ/Э^, = tY, где t — показатель степени однородности.

В случае двухфакторной модели это означает, что:

tQ-Lx MP_L + KxMP_K. (5.20)

Эти два свойства однородной производственной функции особенно важны при анализе издержек (см. главу 6), а также при изучении распределения дохода в конкурентной экономике.

Эластичность выпуска и отдача от масштаба. Если считать формой произ­водственной функции длительного периода степенную функцию:

Q = AL^aKb при а + Ъ = 1, то

показатели а и Ь равны коэффициентам эластичности по факторам:

_ MP_L _ aAK^L"-' _ ^bQl~ AP_L~ ARtLT¹ ~°" _ MP_K РЛГХ^М

AP_K AL^aK^

Для характеристики отдачи от масштаба используется коэффициент эластич­ности выпуска от масштаба (е„_к). Данная величина показывает, на сколько из­менится выпуск, если темп роста объемов использования обоих факторов увели­чится на единицу:

dQ К
^■" ⁼ dK-Q- (5.21)

Коэффициент эластичности выпуска от масштаба характеризует степень од­нородности производственной функции, т. е. отдача от масштаба может быть представлена в универсальной форме:

Q,Ke&-Q(tL,tK). (5.22)

Если показатель степени (е„_£):

♦ >1, то отдача от масштаба возрастает;

♦ = 1, то отдача от масштаба постоянна;

♦ <1 то отдача от масштаба снижается.

Теорема Викселя-Джонса: эластичность выпуска от масштаба равна сумме эластичностей выпуска от используемых факторов:

^еш = ^е<ц.^{+ е}ак- (⁵-²³)