
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Количественный подход: теория предельной полезностиСодержание книги
Поиск на нашем сайте Втемяшилась в башку идея мне: Начну-ка жить с собой наедине. Уйду в себя — других не позову — Кому какое дело, как живу. Сказал — и сделал. Тихий островок Воображеньем создал в краткий срок. Я на своем интимном островке Живу без осложнений, налегке. И если ТАМ - условностей не-счесть, То здесь — лафа! — живу, какой уж есть. (1969) А. Д. Бадаев Иеремия Бентам (1774-1832), о котором основоположник пролетарской политэкономии К. Маркс безапелляционно отозвался как о «трезво-педантичном, тоскливо-болтливом оракуле пошлого буржуазного рассудка»,4 ввел в экономическую 1 Allyon Т., Azrin N. Н. The Measurement and Reinforcement of Behavior of Psychotics // 2 Cardinalis (лат.) — количественный. 3 Ordinalis (лат.) — порядковый. 4 См.: К. Маркс. Капитал. Т. 1. М., 1978. С. 623. Глава 4. Теория индивидуального потребления теорию категорию «полезность» (англ. — «utility»). Люди покупают блага потому, что получают от их потребления удовлетворение (satisfaction). Экономисты называют это удовлетворение полезностью. Индивид стремится максимизировать полезность. Однако полезность — категория сугубо субъективная. Как возможно измерять и сопоставлять между собой полезности различных благ и наборов? Для решения этой проблемы сторонники количественного подхода ввели в научный оборот понятие «ютиль» — гипотетическую единицу полезности. Ютиль (util) — вымышленная единица измерения удовлетворения от потребления блага. Общее удовлетворение от всех единиц (наборов) потребляемых благ в данный период времени называется общей полезностью (TU — total utility). Функцию полезности можно выразить следующим образом: TU = f(QA,QB,...,Qz), (4.1) где QA, QB,— Qz — объемы потребления товаров А, В,... Zb единицу времени. Большой вклад в изучение полезности внесли представители австрийской школы. Они обосновали положение о том, что количество продукта является одним из главных факторов, влияющих на цену в условиях ограниченности ресурсов. Излюбленным приемом для иллюстрации идей экономистов австрийской школы являлось вымышленное замкнутое хозяйство Робинзона Крузо на необитаемом острове. К примеру, полезность одного мешка пшеницы для Робинзона весьма высока: данная пшеница нужна отшельнику, чтобы прокормить себя. Полезность второго мешка пшеницы несколько ниже: зерно пойдет на семена. Полезность третьего мешка еще ниже: Робинзон пустит это зерно на производство сладостей, водки и прочих изысков. Полезность четвертого мешка еще ниже: зерно предназначено для корма для любимого попугая. Полезность пятого мешка еще ниже. Зерно пбйдет на пополнение запасов на «черный день». Полезность шестого мешка — нулевая. Полезность седьмого мешка будет уже отрицательной величиной, так как его негде хранить. И хотя общая полезность зерна (сумма всех мешков) возрастает, предельная полезность (полезность каждого последующего мешка) при этом падает. Графически общая полезность изображена на рис. 4.1. Общая полезность увеличивается до определенной величины Q{ (E — точка максимума, она же — точка насыщения), после которой начинает уменьшаться («полезность» превращается во «вредность»). Уменьшение общей полезности начиная с определенного объема продукта возникает потому, что экономический субъект не способен потребить увеличивающийся объем благ, а условий для их хранения не имеется. Отметим, что до достижения определенного объема Q^ увеличение общей полезности (рис. 4.1) может происходить как затухающими темпами (отрезок 0DC), так и ускоряющимися темпами (отрезок 0.8С). С общей полезностью тесно связана одна из ключевых микроэкономических категорий: предельная полезность. Предельная полезность {MU — marginal utility) — прирост общей полезности блага при увеличении потребления блага на одну единицу. Часть I. Основы рыночного анализа
Рис. 4.1. Изменение общей полезности Предельную полезность можно выразить как с помощью формулы дискретных приращений (4.2), так и в виде частной производной общей полезности (4.3):
ATU (4.2) да
эти 3Q' Геометрически значение предельной полезности в точке А' (длина отрезка OF на нижнем рис. 4.2, я) равно тангенсу наклона касательной к кривой TU (на верхнем рис. 4.2, а) в точке А. В точке В (рис. 4.2, а) величина общей полезности достигает своего максимума, а величина предельной полезности — нуля. Далее с увеличением количества потребляемого блага общая полезность снижается, а предельная полезность становится величиной отрицательной. Рисунок 4.2, б иллюстрирует подобные взаимозависимости между общей и предельной полезностью для случая, когда предельная полезность сначала возрастает, достигая максимума в точке С, а затем начинает снижаться. Основные свойства кривых TV и MU сводятся к следующему: ♦ Кривая TU исходит из начала осей координат: при нулевом потреблении общая полезность равна нулю. ♦ При достижении TU своего максимума значение MU равно нулю. ♦ Значения MU отрицательны при снижении TU. ♦ Значение MU достигает максимума в точке перегиба (С) кривой TU на ее возрастающем участке. ♦ Обычно кривая MU имеет отрицательный наклон, однако встречаются случаи, когда некоторая ее часть (на начальной стадии) наклонена положительно (рис. 4.2, б). Глава 4. Теория индивидуального потребления
сена.
Первый закон Госсена: полезность каждой последующей единицы блага, получаемой в данный момент, меньше полезности предыдущей единицы (предельная полезность блага убывает с увеличением потребления).
Математически первый закон Госсена выражается в том, что первая производная функции общей полезности по количеству данного блага положительна, а вторая производная — отрицательна: d7T/(Q,)>0 a27I/(Q,) <Q
Э# (4.4) Если на начальной степени предельная полезность первоначально увеличивается (отрезок ОВС на рис. 4.1 или ОС на рис. 4.2, б), то в данном частном случае первый закон Госсена не выполняется, ибо:
____________________ Э0_ ' э$ 1 Г. Госсен (1810-1859) — немецкий экономист. Часть I. Основы рыночного анализа В каких случаях в реальной жизни возможно такое исключение? Представим, что врач прописал больному ежедневно потреблять шесть таблеток лекарства в один прием. Можно предположить, что полезность потребления до шести единиц лекарства будет возрастать.
|
||||||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 327; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.007 с.) |

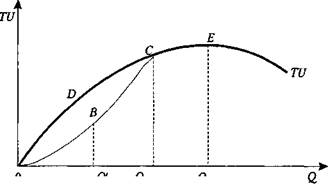
 Рис. 4.2. Изменение общей и предельной полезности Принцип убывающей предельной полезности называется первым законом Гос-
Рис. 4.2. Изменение общей и предельной полезности Принцип убывающей предельной полезности называется первым законом Гос-


