Объем выпуска при разных производственных процессах

На всех себя не хватит Чего они хотят? Чего хочу я? На себя Не хва! На всех.

Мирон Бялошевский (1922-1983)

Производственный процесс может быть определен как специфическая про­порция комбинации затрат для обеспечения определенного объема выпуска. Например, час труда одного рабочего и одной машины сформирует производствен­ный процесс двухфакторной модели труд-капитал. Два рабочих и одна машина — другой производственный процесс и т. д.

Предположим, что фирма может выбирать из трех производственных процес­сов, в которых отношения между капиталом (К) и трудом (L) находятся в про­порциях: 4:1; 1:1 и 1:4. Допустим также, что эти производственные процессы спо­собны давать объемы выпуска соответственно равные: 2, 1 и 2 ед., как это изображено в табл. 5.1 и на рис. 5.1.

Предполагается, что три рассматриваемые нами производственные функции имеют постоянную отдачу от масштаба. Постоянная отдача от масштаба озна­чает, что объем производства возрастает в прямой пропорции с увеличением факторов производства}

Отдача от масштаба (returns to scale) — отношение между темпами изменения вы­пуска и одинаковым для всех факторов темпом изменения объема их использова­ния.

¹ На практике явление постоянной отдачи от масштаба маловероятно. Обычно по мере увеличения количества применяемого фактора производства на начальных стадиях выпуск возрастает ускоренно, а затем, достигнув некой величины, — замедленно (см. рис. 5.4), и, наконец, при преодолении определенного максимума объем выпуска начинает снижаться с дальнейшим увеличением переменного фактора производства. Далее (параграф 5.10) мы рассмотрим проблему переменной отдачи от масштаба подробнее.

Глава 5. Фирма и теория производства

Таблица 5.1 Параметры трех производственных процессов

 

Производственный процесс	Первый	Второй	Третий
L (труд) К (капитал) Объем выпуска	4 2	4 1	4 1 2

Q

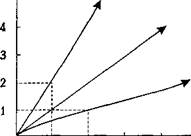
Вариант первый: Qi (Kq, L) = 21 (при K/L -

= 2 Vl)

Вариант второй: Q₂ - 1 (К₀,1) - У₄1 (при КД - Vl)

Вариант третий: Оз ⁼ 2 (К₀, L) = У₂1 (при А/1 = V ₄)

Рис. 5.1. Производственная функция для краткосрочного периода с постоянной отдачей от масштаба {внимание: не путать с рис. 5.2, на котором по оси ординат — К)

Теперь рассмотрим, как изменяется объем выпуска при изменении перемен­ного фактора.

Объем выпуска при замене

Эх, машина миллионная, Дорогая электроника, кнопки красные, зеленые — Это вещь не для дальтоника. В ней идут процессы тайные, Непонятные движения — То сложенье—вычитание, То деление—сложение.

Факторов

А когда уходят на ночь Все сотрудники с работы, Счетовод Степан Степаныч Достает из сейфа счеты. И, согласно указаниям, Он на счетах — дело тонкое -Проверяет показания, Чудо-техникою данные.

(1989) В. Е. Бохнов

Производственная функция, учитывающая процесс изменения одного факто­ра на другой, изображена на рис. 5.2. Из начала координат проведены три луча. Первый луч иллюстрирует производственную функцию Q, = 21 (при K/L = 4/1). В данном случае при постоянной отдаче от масштаба комбинация 24 ед. капитала и 6 ед. труда дает 12 ед. выпуска (точка А).

Во втором производственном процессе (луч 2, производственная функция Q₂ = L, при K/L = 1/1)12 ед. каждого фактора производства также дадут 12 ед. выпуска (точка В).

Часть I, Основы рыночного анализа

В третьем производственном процессе (луч 3, производственная функция Q₃ = 1/2 L при K/L =1/4) комбинация 6 ед. капитала и 24 ед. труда также даст 12 ед. продукции (точка С).

Итак, точки А, В и С представляют одинаковые объемы выпуска (Q, = Q₂ = Q₃= = 12), но представляют собой разные производственные процессы. Соединяющая данные точки «кривая» (ABC), аналогичная кривой безразличия потребителя, получила название изоквантпы.'

К

О 6 12 18 24 L

Рис. 5.2. Процессы производства при разных сочетаниях ресурсов {внимание: не путать с рис. 5.1, на котором по оси ординат — О)

Изокванта (линия равного выпуска — isoquant) — кривая, представляющая множе­ство комбинаций факторов производства (ресурсов), обеспечивающих одинаковый выпуск продукции.²

На отрезке АВ при замене одной единицы труда на две единицы капитала объем выпуска не изменяется. Таким образом, в данном случае предельная норма технического замещения (MRTS) труда на капитал равна двум.

Предельная норма технического замещения (MRTS — marginal rate of technical substitution): пропорция, в которой один фактор может быть заменен на другой при сохранении прежнего объема выпуска; наклон кривой изокванты определяется ве­личиной MRTS.

Замена процесса производства 1 процессом 2 означает переход к более трудо-интенсивному процессу от более капиталоинтенсивного.

На отрезке между точками В и С процесс производства 2 заменяется процессом 3. В данном случае для замены одной машины требуются 2 ед. труда: предельная нор-

¹ Слово «изокванта» состоит из греческого компонента хаоС, («изос» — равный) и ла­
тинского quantitas — количество.

² Изокванты для процесса производства означают то же, что и кривые безразличия для
процесса потребления. Они обладают аналогичными свойствами: отрицательный наклон, вы­
пуклость относительно начала координат, непрерывность и непересекаемость друг с другом.

Глава 5. Фирма и теория производства

ма технического замещения (MRTS) труда на капитал уменьшилась (с 2 до 1/2). Таким образом, изокванты, как и кривые безразличия, выпуклы к началу координат. А это означает, что при движении вдоль кривой вправо величина MRTS уменьшае­тся. Принцип уменьшения MRTS связан с законом убывающей отдачи: каждая до­полнительная единица фактора производства приносит все меньшую отдачу.

MRTS - 2

переменная

L О L О Рис. 5.3. Возможные конфигурации изоквант Предельная норма технического замещения может быть выражена следующим образом: АК MRTSLK = —, или (5.5)

К

 

 

I		б)
	х-	MRTS -> оо / / /MRTS = 0
/	>
.''	---------------- ►

 

MRTS_LK =

 

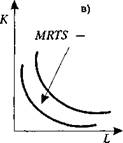
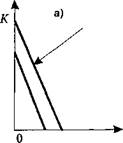
(5.6)

Изокванты, как и кривые безразличия, могут принимать разные формы. На рис. 5.3 изображены три вида изоквант:

♦ линейная с совершенной замещаемостью производственных ресурсов (рис. 5.3, а);

♦ с жесткой дополняемостью ресурсов, которую также называют изоквантой леонтьевского¹ типа (рис. 5.3, б);

♦ с непрерывной, но несовершенной замещаемостью (рис. 5.3, в).