Метод высотных линий положения: высотная изолиния, высотная линия положения, ее элементы и точность.

Метод высотной ЛП является частным случаем общей теории ЛП, когда изолиния является кругом равных высот.Высотная изолиния – круг с центром в полюсе освещенности светила (h=90°) и радиусом r=90°-h.т.А–полюс освещенностиКоординаты А (j_А=d^*,l_А=t_ГР^*).

Предположим, что наблюдатель находится в точке М с координатами j и l, которые ему не известны и которые предстоит определить с достаточной точностью. В этой точке он измеряет высоту h светила С.

Зная высоту светила можно провести круг равных высот с радиусом z = 90° - h. Разумеется, точка М будет находиться где-то на этой окружности.При этом наблюдателю известны счислимые (приблизительные) координаты j_С и l_С точки. Из параллактического треугольника можно рассчитать счислимые высоту и азимут светила:

Эту высоту наблюдатель измерил бы, если б находился в точке М_С. Через эту точку так же можно провести круг равных высот с радиусом z_С = 90° - h_С. Разность n = h – h_C даст нам расстояние в милях между действительным и счислимым кругами равных высот. Проведя азимут А_С на светило и отложив на нём со своим знаком расстояние n, мы найдём определяющую точку К на действительном круге равных высот. Проведя через неё перпендикуляр, мы получим Высотную Линию Положения (ВЛП).

Измерив высоту другого светила и произведя аналогичные расчёты, мы получим вторую ВЛП. Пересечение обоих ВЛП даст нам обсервованное место судна М₀.

Учитывая то, что радиус круга равных высот, как правило, на несколько порядков больше расстояния между точками М_С и М, замена дуги на прямую линию практически не отразится на точности расчётов. То есть мы можем считать, что полученная нами точка М₀ практически совпадёт с действительной точкой М.

В настоящее время метод ВЛП является общепринятым и наиболее распространённым астрономическим методом ОМС.

Из параллактического треугольника по формуле cos стороны получим уравнение высотной изолинии:

cos(90°-h)=sinh=sinj*sind+cosj*cosd*cos(t_ГР+l)

Касательная или секущая к высотной изолинии в районе счислимого места называется высотной ЛП. Согласно обобщенного метода линий положения элементами высотной линии положения являются перенос n и азимут А_С.

n=DU/g=h_O-h_C=Dh

t - направление градиента, совпадает с азимутом на светило, т.е. t=А_С.

Уравнение ВЛП имеет вид: Dh=DjcosA+DlcosjsinA, где Dj, Dl - поправки к счислимым координатам для получения обсервованных, т.е. j_О=j_С+Dj, l_О=l_С+Dl.

Аналитически место судна можно определить, рассчитав по формулам:

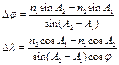
Метод ВЛП имеет некоторые недостатки:

- при больших высотах светила, особенно при h>88°, происходит большое отклонение ВЛП от высотной изолинии, так как уменьшается радиус круга равных высот. Поэтому в таких случаях замена круга равных высот ВЛП нецелесообразна - при больших переносах прокладка азимута прямой линией неправомерно за счет искривления земной поверхности, что особенно существенно в больших широтах.

Эти недостатки начинают оказывать влияние на точность ОМС при Dh>30’. В это случае обсервованное по ВЛП место судна принимается за счислимое и выполняется второе приближение.

Точность ВЛП.

Примем в уравнении ВЛП Dh=±m_Dh±D - ошибка в переносе, Dj=m_jо, Dl=m_lо - ошибки в обсервованных координатах возникающие вследствие действия ошибки в переносе. Тогда получим уравнение ошибок: ±m_Dh±D= m_jоcosA+ m_lоcosjsinA, где m_Dh – случайные ошибки переноса, D - систематические ошибки переноса.

,

m_ho=0,3’¸1,2’, т.к. m_hс=±0,1’¸0,2’ по таблицам или ВТ, то m_Dh=0,7²+0,2²» m_ho

Таким образом получаем, что точность ВЛП зависит от точности измерения высоты светила. Ошибки измерения высоты светила смещают ВЛП пропорционально своей величине по закону нормального распределения случайных величин.