Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Распределение эмпирических данных и процедуры его анализаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В результате измерения накапливается совокупность значений свойства, выраженных в определенной шкале. Закономерность, с которой данные значения представлены на всем пространстве шкалы, называется распределением[51]. В работах Ф. Гальтона впервые было установлено, что психологические явления подчиняются закону нормальности распределения, т. е. могут быть описаны формулой:
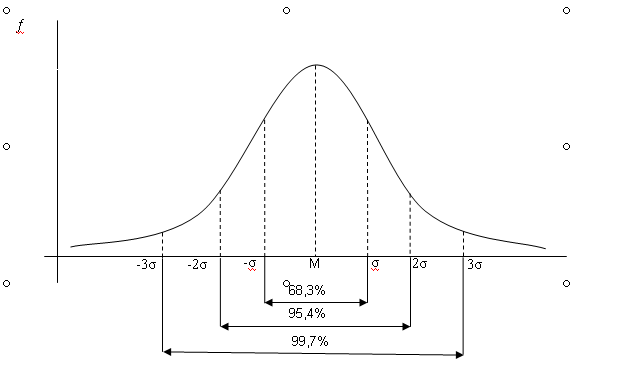
где Мх (математическое ожидание) и σ 2х (дисперсия) – параметры распределения; λх – интервал группировки данных (отличный от единицы); π = 3,14…; е = 2,17. Данная формула претерпела множество изменений, прежде чем утвердилась в своем окончательном виде в психологии. П. Лаплас сформулировал функцию симметричного распределения интегральных вероятностей, послужившего фундаментом для работ Ф. Гаусса, открывшего закон распределения вероятностей – закон нормального распределения, что было подтверждено работами А. Кеттле. Кеттле указывал, что средняя величина встречается в совокупности измерений чаще, чем отклоняющаяся от среднего. Причем чем больше это отклонение, тем реже данная величина встречается. Графически это показано на рис. 1. Интервал М ± σ описывает площадь под кривой, в которую входит 68,3 % проявлений психического явления. Интервал М ± 2σ – 95,4 %, а интервал М ± 3σ соответствует 99,7 % площади. Таким образом, кривая нормального распределения описывает частоту интенсивности изучаемого психического явления и представляет собой графическое выражение формулы (3). Важное следствие закона о нормальности распределения – возможность стандартизации измерений, т. е. графически, приведения их к некоей стандартной, эталонной кривой. Так как результаты любого измерения могут быть выражены через М – среднее и σ – стандартное отклонение, то возникает возможность стандартизации измерения согласно формуле (4):
где Z = стандартизованное значение; х i – значение переменой, значение среднего для х. Полученное распределение характеризуется следующими свойствами: – среднее (М) для такого распределения = 0, σ = 1; – кривая приближается к оси z асимптоматически; – кривая симметрична при М = 0, ее асимметрия и эксцесс равны 0; – площадь между кривой и осью z равна 1. Алгоритм приведения к нормальному виду, по О. А. Попову, выглядит следующим образом, учитывая, что при нормальном распределении в интервал m ± 1σ попадает 68,26 % всей выборки, этот интервал и принимается за средние баллы. Все значения до него относятся к низким, а выше него – к высоким. Таким образом, получаем три градации баллов. Для подобной стандартизации можно использовать интервал m ± 2/3σ, тогда 50 % выборки попадает в средние и по 25 % – в низкие и высокие баллы. Каким будет интервал – выбирает сам исследователь. Разделение на 4 интервала осуществляется подобным образом, граница между вторым и третьим интервалом проходит по среднему арифметическому. Разделение на пять уровней применяется при сильном разбросе данных. В подобном случае добавляется интервал m ± 2σ. Недостатком «уровневой» стандартизации является то, что полученные уровни с трудом поддаются последующей статистической обработке и слишком малоинформативны. Применение закона нормальности распределения – важный этап при проведении математико-статистической обработки эмпирических данных.
Рис. 1. Кривая нормального распределения М – среднее значение, σ – стандартное отклонение, Именно характер распределения определяет стратегию дальнейшего анализа данных. Так, если эмпирическое распределение соответствует нормальному, возникает возможность применения параметрических методов статистического анализа. В обратном случае используются непараметрические методы. Причины несоответствия полученного распределения нормальному могут заключаться как в объективной природе регистрируемого явления, так и в самой процедуре измерения. Вопрос о нормальности распределения значений психических явлений актуален на протяжении всего периода применения математических методов в психологии. К примеру, И. Кант отрицал возможность применения статистического анализа для изучения психических явлений, утверждая, что человеческая душа метафизична и не может подлежать формальному исследованию. Противники этой точки зрения утверждают, в свою очередь, что без эксперимента, процедуры измерения психология не может являться подлинно научной дисциплиной. Процедура исследования, в свою очередь, влияет на нормальность распределения, к примеру, в связи с неравномерной «чувствительностью» инструментария. Таким образом, при изучении умственных способностей путем решения задач, ряд из них может быть неразрешим или, наоборот, чрезвычайно прост для испытуемых. В подобном случае на графике распределения будет отражена асимметрия (смещение) линии графа от среднего в сторону меньших или больших значений. Показатель эксцесса (плосковершинности или остроты) графика распределения свидетельствует о преобладании определенного частотного диапазона значений изучаемого явления по выборке. Проверка полученного распределения на нормальность базируется на вычислении ряда дескриптивных статистик. Дескриптивная (описательная) статистика – это различные статистические показатели, описывающие распределение данных. К ним относятся среднее, мода, медиана, разброс, дисперсия и стандартное отклонение. Среднее (арифметическое) вычисляется по формуле:
где х i – значение изучаемого явления (i указывает на порядковый номер зафиксированного значения); n – количество наблюдений. Мода (Мо) – наиболее часто встречающееся значение признака в выборке. Мо вычисляется определением частоты ƒ встречаемости признака. В случае если несколько близких членов ряда обладают одинаковой частотой встречаемости, то Мо выборки определяется их среднеарифметическим значением. В выборке могут существовать несколько мод, в данном случае выборка является бимодальной, или есть возможность выделения генеральной моды и нескольких локальных. Медиана (Md) – значение признака, разделяющее выборку на две симметричные части. Md определяется путем ранжирования значений по выборке. В случае, если количество значений нечетное, то медиана – центральное (симметричное) значение, в противном случае медиана – среднее арифметическое нескольких центральных значений. Разброс (R) определяет разброс значений по выборке от максимального к минимальному. Разброс вычисляется вычитанием из максимального значения минимального. Дисперсия – мера рассеивания значений изучаемого явления (признака), характеризующая степень разобщенности измеряемых значений вокруг среднего.
где n – количество измерений; Х – среднее арифметическое, вычисляемое по формуле (5). Стандартное отклонение (σ) – среднее квадратическое отклонение, вычисляемое путем выделения квадратного корня из дисперсии:
Вычисление среднеквадратического отклонения – важный этап проверки предположения о нормальности распределения, принятия решения о выборе метода последующей статистической обработки данных. Коэффициент вариации (V) есть отношение стандартного отклонения к среднему арифметическому значению, выраженное в процентах:
где s – среднеквадратическое отклонение; Х – среднее арифметическое вариативного ряда. Коэффициент вариации используется для характеристики однородности исследуемой совокупности. Статистическая совокупность считается количественно однородной, если коэффициент вариации не превышает 33 %[52]. Исследование формы распределения. Выяснение общего характера распределения предполагает не только оценку степени его однородности, но и исследование формы распределения, т. е. оценку симметричности и эксцесса. В статистике различают одновершинные и многовершинные виды кривых распределения. Однородные совокупности описываются одновершинными распределениями. Многовершинность распределения свидетельствует о неоднородности изучаемой совокупности или о некачественном выполнении группировки[53]. Одновершинные кривые распределения делятся на симметричные, умеренно асимметричные и крайне асимметричные. Распределение называется симметричным, если частоты любых 2 вариантов, равноотстоящих в обе стороны от центра распределения, равны между собой. В таких распределениях x = Mo = Me. Асимметрия – показатель, отражающий перекос распределения относительно среднего арифметического влево или вправо. В тех случаях, когда какие-нибудь причины влияют на появление значений, которые выше или, наоборот, ниже среднего, образуются асимметричные распределения[54]. На графике распределения, таким образом, будет отражена асимметрия (смещение) линии графа от среднего в сторону меньших или больших значений. Положительно асимметричным считается распределение с более крутым левым и более пологим правым крылом, распределение с отрицательной асимметрией, напротив, имеет более пологий левый фронт нарастания и более крутой правый (см. рис. 2).
Рис. 2 Типы асимметрии Рассчитываемый по соответствующим формулам коэффициент асимметрии (As) может быть использован в качестве одного из критериев соответствия экспериментального распределения теоретическому. Вычисление коэффициента асимметрии: Коэффициент асимметрии вычисляется по следующей формуле:
где zx – мера Пирсона
Соответствие эмпирического распределения нормальному находится по таблицам соответствующих распределений. При этом эмпирическое распределение считается соответствующим теоретическому (нормальному), если асимметрия при данной выборке не превышает граничного значения. Причины асимметрии могут быть различными. Во-первых, это возможное действие побочных однонаправленных факторов. Так, например, в тестах на измерение интеллекта могут преобладать сложные задания, с которыми большинство испытуемых не справляется. Это может явиться причиной положительной асимметрии (центральная тенденция лежит слева от среднего значения). Во-вторых, это ограничение (сверху или снизу) размаха вариаций. Например, при измерении времени сенсомоторной реакции нижний предел реагирования лимитирован физиологическими возможностями субъекта, в то время как верхний жестко не ограничен. Наконец, третьей причиной асимметрии может быть неоднородность выборки (например, если исследование проводится в смешанной группе разного возраста). При этом имеет место наложение друг на друга двух или нескольких разных по численности и сдвинутых относительно друг друга по моде распределений. Показатель эксцесса (плосковершинности или остроты) графика распределения свидетельствует о преобладании определенного частотного диапазона значений изучаемого явления по выборке. В отличие от коэффициента асимметрии, коэффициент (показатель) эксцесса характеризует компактность или «размытость» распределения, его островершинность или плосковершинность, что связано с разным характером группирования значений переменной вокруг среднего (рис. 3).
Рис. 3. Типы эксцесса Причинами эксцесса могут быть большая или меньшая степень тяготения переменных к центральной тенденции, неоднородность выборки, наложение друг на друга нескольких распределений с одинаковой модой и разной дисперсией и т. д. Вычисление показателя эксцесса:
Теоретически, величина эксцесса может варьироваться от – 3 до + ¥. Критерий согласия с нормальным распределением аналогично коэффициенту асимметрии определяется по таблицам граничных значений. Аналогично определению асимметрии распределение соответствует нормальному (согласуется с нормальным), если Ex < Exкр. При обратном соотношении принято говорить, что по показателю эксцесса эмпирическое распределение статистически достоверно отличается от нормального. При анализе эмпирического распределения может возникнуть такая ситуация, когда по одному из показателей (асимметрии или эксцессу) распределение соответствует нормальному, по другому же – отличается от него. В этом случае следует использовать следующее правило: если хотя бы по одному из вышеуказанных показателей распределение достоверно отличается от нормального, то следует делать вывод о том, что экспериментальное распределение отличается от теоретического (нормального). Кроме коэффициента асимметрии и показателя эксцесса, для сравнения экспериментального распределения с теоретическим используют и другие критерии, в частности критерий хи-квадрат и критерий l Колмогорова – Смирнова. Вычисление дескриптивных показателей – важный этап математико-статистического анализа, позволяющий с минимальными временными затратами дать общую описательную характеристику особенностей проявления изучаемого показателя в выборке. Объективность психологического измерения зависит от особенностей стандартизации, свойств валидности и надежности применяемого психодиагностического метода. Стандартизация подразумевает единообразие измерения тестового материала, процедуры проведения теста и его оценки. Процедура стандартизации включает разработку точных инструкций относительно используемых материалов; ограничения времени; формулирования устных инструкций испытуемому; указаний, касающихся предварительных предъявлений теста; способов трактовки вопросов со стороны испытуемого и других деталей проведения теста. На этапе разработки теста, а также любого другого метода проводится процедура стандартизации, которая включает три этапа. Первый этап стандартизации психологического теста состоит в создании единообразной процедуры тестирования. Она включает определение следующих моментов диагностической ситуации: – условия тестирования (помещение, освещение и другие внешние факторы); – содержание инструкции и особенности ее предъявления (тон голоса, паузы, скорость речи и т. д.); – наличие стандартного стимульного материала; – стандартный бланк для выполнения данного теста; – учет влияния ситуационных переменных (состояние испытуемого (усталость, перенапряжение и т. д.), нестандартные условия тестирования (плохое освещение, отсутствие вентиляции и др., прерывание тестирования) на процесс и результат тестирования; – учет влияния поведения диагноста на процесс и результат тестирования; – учет влияния опыта респондента в тестировании. Следующий этап стандартизации психологического теста состоит в создании единообразной оценки выполнения теста: стандартной интерпретации полученных результатов и предварительной стандартной обработки. Важным этапом стандартизации психологического теста выступает определение норм выполнения теста. Норма – это усредненное значение тестового показателя, полученное в ходе измерения. В психологической диагностике существует несколько вариантов нормирования показателей теста[55]: 1) приведение к нормальному виду; 2) приведение к стандартной форме; 3) квантильная стандартизация. Для определения способа преобразования обычно рассматриваются гистограммы распределения первичных тестовых оценок. Они позволяют выявлять лево- и правостороннюю асимметрию, положительный или отрицательный эксцесс и другие отклонения от нормальности. Под приведением к стандартной форме понимают линейное преобразование нормальной (или искусственно нормализованной) тестовой оценки следующего вида:
где Zi – стандартная тестовая оценка i-го испытуемого, х i – нормальная оценка i-го испытуемого, Мх и σх – среднее арифметическое значение и среднеквадратическое отклонение х. Стандартные Z-оценки распределены по нормальному закону с нулевым средним и единичной дисперсией, что способствует проведению сравнительного анализа стандартных оценок различных психодиагностических показателей. Нормализованные стандартные показатели, полученные с помощью нелинейного преобразования, – это стандартные показатели, соответствующие распределению, преобразованному так, что оно принимает вид нормального. Для их расчета создаются специальные таблицы перевода сырых баллов в стандартные. В них приводится процент случаев различных степеней отклонений (в единицах σ от среднего значения). Так, среднее значение, которое соответствует достижению 50 % результатов группы, может приравниваться к 0. Среднее значение минус стандартное отклонение может быть приравнено к –1, это новое значение будет наблюдаться примерно у 16 % выборки, а значение +1 – примерно у 84 %. На этой основе строятся станайны и стэны. Станайн (среднее = 5, σ = 2) – это стандартизованный показатель, благодаря которому нормальное распределение разбивается на девять интервалов таким образом, что 1-й и 9-й станайны содержат по 4 % выборки, 2-й и 8-й – по 7 %, 3-й и 7-й – по 12 %, 4-й и 6-й – по 17 %, 5-й – 20 %. Для перевода в стэны можно использовать формулу стандартизации, но чаще всего используют более формальную процедуру: находят среднее (m), стандартное отклонение (σ), от среднего в обе стороны отсчитывают по пять интервалов по σ /2 (половине σ). Получившиеся 10 интервалов и являются стэнами. Выбор типа шкалы зависит от исходных данных. Если сырой балл принимает значения от 0 до 100, и он стандартизуется в стэны или станайны, то явно теряется значительное количество информации, т. к. внутри одного стандартного интервала может находиться достаточно много «сырых» баллов, что неприемлемо. Поэтому при большом диапазоне «сырых» баллов используются Т-баллы. Стандартизация может происходить и без участия стандартных и известных всем шкал, а основываться на любых произвольных значениях среднего и стандартного отклонения, полученного на выборке. Многие тесты познавательных способностей, а также некоторые личностные опросники используют нелинейное преобразование при стандартизации полученных «сырых» значений. Достоинство нелинейного преобразования в том, что психологу не нужно задумываться, как распределены баллы теста – нормально или нет. Типичной нелинейной шкалой являются процентили, получившие очень широкое распространение в психодиагностике за счет своей наглядности и простоты восприятия. Процентиль – это процент значений в выборке, меньших либо равных конкретно взятому значению. В психологии применяются несколько исторически устоявшихся вариантов шкал стандартизации: – шкала Т-баллов Мак-Колла – Х = 50, σ = 10; – шкала IQ – Х = 100, σ = 15; – шкала «станайнов» (целочисленные значения от 1 до 9) – Х = 5, σ = 2; – шкала «стэнов» (Кеттелла) – Х = 5,5, σ = 2. Перевод из шкалы в шкалу осуществляется по формуле:
Под квантильным преобразованием понимается процентильная стандартизация, когда отметке «сырой» шкалы х i присваивается новое значение ее процентильного ранга PR (х i). Квантиль является общим понятием, частными случаями которого кроме процентилей могут быть, например, квартили, квинтели и децили. Три квартильные отметки (Q1, Q2, Q3) разбивают эмпирическое распределение тестовых оценок на 4 части (кварты) таким образом, что 25 % испытуемых располагаются ниже Q1, 50 % – ниже Q2 и 75 % – ниже Q3. Четыре квинтеля (K1, К2, К3, К4) делят выборку аналогичным образом на 5 частей с шагом 20 %. Девять децилей (D1 … D9) разбивают выборку на десять частей с шагом 10 %. Номер соответствующего квантиля используется в качестве новой преобразованной тестовой оценки. Квантильная шкала отличается тем, что ее построение никак не связано с видом распределения первичных тестовых оценок, которое может быть нормальным или иметь любую другую форму. Единственным условием для ее построения является возможность ранжирования испытуемых по величине х. Стандартизация тестовых оценок путем их перевода в квантильную шкалу стирает различия в особенностях распределения психодиагностических показателей, т. к. сводит любое распределение к прямоугольному (равномерному). Поэтому с позиции теории измерений квантильные шкалы относятся к шкалам порядка: они дают информацию относительно того, у кого из испытуемых сильнее выражено тестируемое свойство, но ничего не позволяют сказать о том, насколько или во сколько раз сильнее. В процессе стандартизации тест проводится на большой выборке испытуемых того типа, для которого он предназначен. Эта группа называется стандартизированной выборкой и служит для установления норм. Важным свойством выборки является репрезентативность, т. е. выборка стандартизации должна максимально точно отражать ту категорию людей, для которой предназначен тест, иначе он не может быть использован для целей диагностики или отбора. Полученные в результате стандартизации тестовые нормы отличаются по степени своей репрезентативности. Чем шире обследованная выборка, чем точнее она отражает структуру генеральной совокупности (по полу, возрасту, уровню образования и т. п.), тем выше репрезентативность тестовых норм.
5. Параметрические и непараметрические процедуры
Для расчета общностей, характеризующихся параметрическим типом распределения, применяются специальные виды корреляционного и сопоставительного анализа. Корреляционный анализ – статистическая процедура установления меры отношения между переменными, при котором рассматриваются форма, знак и теснота связи исследуемых признаков или факторов. Термин «корреляция» впервые вводится Ф. Гальтоном в 1886 г., а как метод статистического анализа начинает применяться К. Пирсоном. При определении формы связи рассматривается ее линейность или нелинейность (т. е. как в среднем изменяется y в зависимости от изменения x, а x – от y). Широкое применение в психологических исследованиях находят также коэффициенты ранговых, частных, частичных, множественных и других коэффициентов корреляции. В табл. 4 представлен широкий спектр методов корреляции, применяемых в зависимости от характера измерения. Таблица 4 Применение коэффициентов корреляции Тип шкалы |
Мера связи | ||||||||||||||||||||||||||||||
| Переменная X | Переменная Y | |||||||||||||||||||||||||||||||
| Интервальная или отношений | Интервальная или отношений | Коэффициент Пирсона | ||||||||||||||||||||||||||||||
| Ранговая, интервальная или отношений | Ранговая, интервальная или отношений | Коэффициент Спирмена | ||||||||||||||||||||||||||||||
| Ранговая | Ранговая | Коэффициент Спирмена | ||||||||||||||||||||||||||||||
| Дихотомическая | Дихотомическая | j – коэффициент Кеттелла | ||||||||||||||||||||||||||||||
| Дихотомическая | Ранговая | Рангово-бисериальный | ||||||||||||||||||||||||||||||
| Дихотомическая | Интервальная или отношений | Бисериальный | ||||||||||||||||||||||||||||||
Расчет коэффициента корреляции по Пирсону нуждается в следующих допущениях:
1. Переменные для анализа должны быть представлены в интервальной шкале или шкале отношений.
2. Распределения полученных эмпирических данных должны быть близки к нормальному.
3. Число измерений для сопоставляемых переменных должно быть одинаковым.
Формула для расчета коэффициента корреляции по Пирсону выглядит следующим образом:
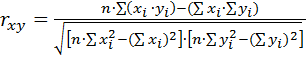 , ,
| (12) |
где х i – значения, принимаемые переменной X;
yi – значения, принимаемые переменной Y;
n – количество переменных.
Данная формула оптимальна при ручном (неавтоматизированном) расчете. Для дальнейшего упрощения можно построить следующую таблицу, заполнение которой способствует вычислению корреляционной связи. Полученные значения в графе «Сумма» табл. 5 необходимо подставить в формулу (12).
Таблица 5
Табличный расчет коэффициента корреляции по Пирсону
| № п/п | X | Y | X·X | Y·Y | X·Y |
| Сумма | Σ x | Σy | Σ x·x | Σ y·y | Σ x·y |
Величина коэффициента линейной корреляции находится в интервале: 1< r < + 1 и не может выходить за его пределы, т. е. равняться или превышать 1 по модулю. Интерпретация полученного коэффициента проводится на основе его фактического выражения по модулю полученного знака и уровня статистической значимости. Коэффициент корреляции, близкий к 1 по модулю, свидетельствует о высоком уровне связи между анализируемыми переменными, близкий к 0 – о низком уровне связи или ее отсутствии на данной выборке.
Знак корреляционной связи описывает характер зависимости. Положительный знак указывает на прямо пропорциональную зависимость, отрицательный – на обратно пропорциональную. То есть в первом случае с изменением одной переменной с определенной долей статистической вероятности можно говорить о последовательном изменении второй (согласованном росте или убывании), во втором случае с уменьшением одной переменной вторая увеличивается (и наоборот).
Заключительным этапом при расчете коэффициента корреляции является определение уровня статистической значимости полученной связи. С этой целью результаты вычислений по формуле (12) сопоставляются с табл. I в прил. 2. В данной таблице представлены критические значения коэффициентов корреляции по Пирсону для выборок от 4 до 1000 элементов (n).
Помимо установления связи между переменными, достаточно часто в психологических исследованиях ставится задача определения различий в выраженности какого-либо признака в связи с влиянием некоторых факторов. С этой целью применяется параметрический критерий t, иначе называемый критерий Стьюдента. Критерий Стьюдента был разработан английским химиком У. Госсетом в ходе работы на пивоваренном заводе Гиннеса. Поскольку по условиям контракта Госсет не имел права открытой публикации своих исследований, поэтому статьи по t-критерию были напечатаны в 1908 г. в журнале «Биометрика» под псевдонимом «Student». В отечественной литературе принято писать «Стьюдент»[56].
Простота вычисления t-критерия Стьюдента, а также его наличие в большинстве статистических пакетов и программ привели к широкому использованию этого критерия даже в тех условиях, когда применять его нельзя. Рассмотрим более подробно особенности использования статистического t-критерия Стьюдента.
Наиболее часто t-критерий используется в двух случаях. В первом случае его применяют для проверки гипотезы о равенстве генеральных средних двух независимых, несвязанных выборок (так называемый двухвыборочный t-критерий). В этом случае есть контрольная и опытная группы, состоящие из разных лиц, их количество в группах может быть различно. Во втором же случае используется так называемый парный t-критерий, когда одна и та же группа объектов порождает числовой материал для проверки гипотез о средних. Поэтому эти выборки называют зависимыми, связанными. Например, психологические свойства одних и тех же лиц до и после психологического тренинга. В обоих случаях должно выполняться требование нормальности распределения исследуемого признака в каждой из сравниваемых групп.
Следующее требование, которое должно выполняться, – это равенство дисперсий в сравниваемых группах. Чем больше различаются между собой дисперсии и объемы выборок, тем сильнее отличается распределение «вычисляемого t-критерия» от распределения истинного «t-критерия Стьюдента». При этом различную величину имеют и сам t-критерий, и такой параметр этих распределений, как число степеней свободы.
В свою очередь, число степеней свободы сказывается на величине достигнутого уровня значимости (р <...), определяемого для вычисленной величины t-критерия. Во многих статистических пакетах величина t-критерия вычисляется для двух случаев: 1) дисперсии равны, 2) дисперсии не равны. При этом предполагается, что в обоих случаях требование нормальности распределения выполняется.
Таким образом, для принятия решения о применении t-критерия Стьюдента к данным следует придерживаться таких критериев:
1. Данные должны быть представлены в шкале интервалов либо отношений.
2. Сравниваемые выборки должны иметь распределение, близкое к нормальному.
3. Сравниваемые выборки должны иметь одинаковый размер.
Формула t-критерия Стьюдента имеет следующий вид:
для несвязанных выборок:
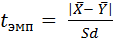 , ,
| (13) |
и
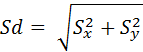 , ,
| (14) |
где
Х – среднее арифметическое для X;
Y – среднее арифметическое для Y;
Sd – сумма среднеквадратических отклонений X и Y.
Число степеней свободы вычисляется для неравных групп: k = n1 + n2 – 2, где n1 – выборка первой группы, n2 – второй; для равных по размеру групп:
k = 2 · n – 2, где n – объем выборки;
для связанных выборок:
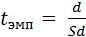 0, 0,
| (15) |
где
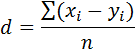
| (16) |
и
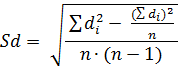
| (17) |
Число степеней свободы вычисляется как k = n – 1, где n – объем выборки. t-критерий Стьюдента без применения пакета статистических программ может быть рассчитан «вручную». С этой целью необходимо заполнить табл. 6. Приведем пример для несвязанных выборок.
Таблица 6
Табличный расчет t-критерия Стьюдента для несвязанных выборок
| № п/п |
Значения по группам |
Отклонения от среднего |
Квадраты отклонений | |||
| X | Y | 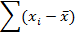
| 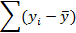
| 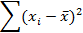
| 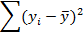
| |
| 1 | ||||||
| Сумма | Σ x | Σy | 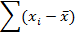
| 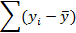
| 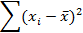
| 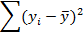
|
| Среднее | 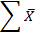
| 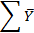
| ||||
Полученные в таблице значения подставляются в формулы (13) и (14).
Непараметрические процедуры математико-статистического анализа. В качестве непараметрического метода изучения корреляционных связей в выборке можно применять коэффициент ранговой корреляции Спирмена. Этот коэффициент определяет степень тесноты связи порядковых признаков, которые представлены в виде рангов сравниваемых величин.
Величина данного коэффициента ранговой корреляции лежит в интервале от –1 до +1. Как и линейный коэффициент Пирсона, может принимать положительные и отрицательные значения, характеризуя, в то же время, направленность связи между признаками, представленными в ранговой шкале.
Расчет коэффициента ранговой корреляции предполагает соблюдение ряда требований:
1. Сравниваемые переменные должны быть представлены в ранговой шкале.
2. Число сопоставляемых признаков должно быть одинаковым.
Формула расчета коэффициента корреляции по Спирмену при отсутствии в выборке одинаковых рангов выглядит следующим образом:
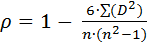 , ,
| (18) |
где
n – объем выборки (количество ранжируемых признаков);
D – разность между рангами по двум переменным для каждого испытуемого;
∑(D 2) – сумма квадратов разностей рангов.
В случае если в выборке находятся одинаковые ранги, в формулу вычисления коэффициентов корреляции добавляются поправки на одинаковые ранги. Изменения претерпевает числитель формулы (18). В случае, если в первой сопоставляемой группе присутствуют одинаковые ранги, в числитель необходимо добавить следующий коэффициент (D1):
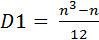 , ,
| (19) |
где n – число одинаковых рангов.
Таким образом, формула (18) модифицируется до:
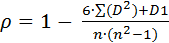 , ,
| (20) |
После вычисления эмпирического значения ρ полученный коэффициент сопоставляется с табличным. Отметим, что табличные значения при расчете коэффициента ранговой корреляции Стьюдента от n = 5 до n = 40 представлены в табл. III прил. 2, при n > 40 справедливы критические значения коэффициента линейной корреляции по Пирсону (табл. IV прил. 2).
Критерий хи-квадрат (х2) распределения используется для расчета согласия эмпирического распределения теоретическому, а также для расчета однородности экспериментальных выборок. При совпадении эмпирического и теоретического распределения величина х2ЭМП = 0, с увеличением этих значений расхождение также увеличивается.
Формула х2:
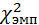 = = 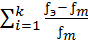 , ,
| (21) |
где
f Э = эмпирическая частота;
fm = теоретическая частота;
k = количество разрядов признака.
Для сравнения двух эмпирических распределений (в зависимости от вида представленных данных) формула для расчета х2 распределения может иметь вид:
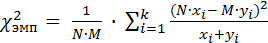 , ,
| (22) |
где N и M – количество элементов в сопоставляемых выборках.
Для расчета уровня значимости х2 распределения используется понятие степени свободы, которое рассчитывается по формуле: v = k – 1, где k – количество элементов в выборке. Таблица критических значений приведена в табл. IV пр
|
| Поделиться: |

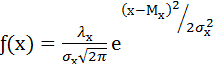 ,
,
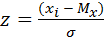 ,
,
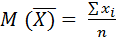 ,
,
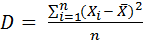 ,
,
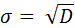
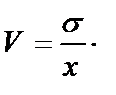 100 %, (8)
100 %, (8)
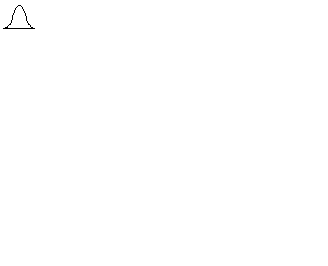
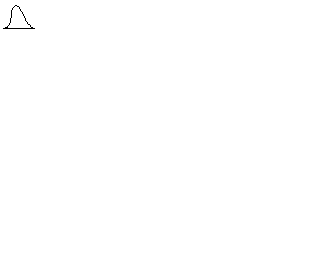
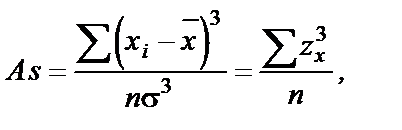 (9)
(9)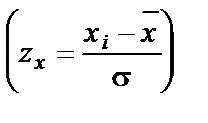 .
. При больших выборках (n > 50) можно использовать упрощенную формулу:
При больших выборках (n > 50) можно использовать упрощенную формулу:


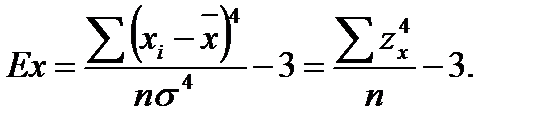 (11)
(11)