
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 1. Понятие, предмет, задачи и структура психодиагностикиСодержание книги
Поиск на нашем сайте
МВД России Санкт–Петербургский университет
К.В. Злоказов
ПСИХОДИАГНОСТИКА
Учебник
Санкт-Петербург 2018 МВД России Санкт–Петербургский университет
К.В. Злоказов
ПСИХОДИАГНОСТИКА
Учебник
Санкт-Петербург 2018 План 2018, поз. 5 УДК 159.9 ББК 88.91 З 68
В учебнике представлены теоретические и практические сведения из курса «Психодиагностика», приводятся методы математико-статистической обработки экспериментальных данных, прилагаются методики психологической диагностики свойств и качеств личности. Учебник будет полезен психологам органов внутренних дел, курсантам, слушателям, адъюнктам и педагогическим работникам образовательных организаций МВД России, а также всем интересующимся вопросами теории и практики психологической диагностики личности. Предназначен для обучающихся по специальности УДК 159.9 ББК 88.91 Рецензенты: Хрусталева Т.А., кандидат психологических наук, доцент (Московский университет МВД России имени В.Я. Кикотя); Таганова А.А., кандидат психологических наук, доцент (Краснодарский университет МВД России) Меркушева О.В., начальник отделения по организации
© Санкт–Петербургский университет МВД России, 2018 ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ.. 4 Тема 1. Понятие, предмет, задачи и структура психодиагностики. 6 Тема 2. История развития психодиагностики. 23 Тема 3. Психодиагностика и смежные направления исследований. 53 Тема 4. Классификация методов психологической диагностики. 73 Тема 5. Этапы психодиагностической процедуры.. 99 Тема 6. Этика психодиагностического обследования. 120 Тема 7. Принципы составления заданий психодиагностической методики. 136 Тема 8. Основные математические процедуры, используемые при создании психодиагностической методики. 166 Тема 9. Виды опросников. 198 Тема 10. Виды тестов. 221 Тема 11. Измерение интеллекта. 243 Тема 12. Проективные методики. 273 Тема 13. Задачи диагностического обследования персонала. 297 Тема 14. Методы диагностического обследования персонала. 327 ЗАКЛЮЧЕНИЕ. 351 СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ.. 352 ПРИЛОЖЕНИЯ.. 353
ВВЕДЕНИЕ
Психологическая диагностика – это отрасль психологической науки, разрабатывающая теорию и методы изучения индивидуальных и социальных особенностей психологии субъекта. Под психодиагностикой также понимается вид деятельности психолога по измерению и оценке особенностей личности. Психодиагностика используется в различных сферах социальной жизни – обучении и развитии, сохранении здоровья и профессионального становления. Психодиагностическая деятельность налагает большую ответственность на психолога. Результаты психологической диагностики используются для оценки и экспертизы, принятия кадровых и судебных решений. Для использования методов психодиагностики необходимо обладать знаниями из нескольких областей психологической науки: а) общепсихологических теорий, б) концепций развития психики и личности, в) социально-психологических моделей взаимодействия личности и общества, г) основ клинической, педагогической и дифференциальной психологии. Данные области образуют фундамент психодиагностики – ее концептуальные основания. Конечно, психодиагностика обладает и собственным знанием. Речь идет о теории психодиагностического исследования, методологии измерения и оценки психологических явлений. Овладение им критически важно для проведения измерений, получения точной и объективной психологической информации. В последние десятилетий наблюдается интенсивное развитие методических и инструментальных средств психодиагностики. Современный специалист способен не только применять методы диагностики но и создавать их, критически оценивать их психометрические свойства, приспосабливать к запросам практической деятельности. Учебник нацелен на формирование целостных представление о научной и практической психодиагностике, передачу знаний о ее теоретических и инструментальных аспектах. Содержание учебника включает описание основных подходов, направлений и концепций психологической диагностики, правил и ограничений использования психодиагностических методов и методик. Учебник предполагает формирование умений организации психодиагностического процесса – от получения диагностического запроса до подготовки заключения. В содержании уделяется внимание профессионально-этическим стандартам деятельности психодиагноста. Отдельные разделы учебника направлены на развитие психометрических компетенций будущих специалистов – способности оценивать валидность и надежность тестов и опросников, стандартизировать результаты их измерения. Содержание сгруппировано в соответствии с тематикой классических учебников по психологической диагностике, под авторством Л.Ф. Бурлачука. Вместе с тем, большинство разделов содержит дополненные и расширенные сведения о теории, методологии и методиках психологического измерения. Для увеличения эффективности процесса подготовки после каждой из глав представлены вопросы, позволяющие самостоятельно оценить уровень знаний. В приложении к учебнику приводятся статистические таблицы, облегчающие выполнение типовых психометрических и статистических операций, связанных с определением мер центральной тенденции, тестированием эмпирических гипотез, расчётом вероятности.
Этап обработки и интерпретации. Подготовка заключения.
Обработка результатов обследования как правило, применяется в отношении количественных методов измерения. Она осуществляется посредством подсчета «сырых» и стандартизированных баллов. Так называемы «сырые баллы» представляют собой первичные показатели, вычисляемые согласно методике расчёта результатов. Например, количество совпадений ответов испытуемого в тесте способностей с указанным разработчиком ключом. Если методика или процедура содержит несколько шкал, то сырой балл рассчитывается для каждой из них. Для методик, предполагающих наблюдение, анкетирование или собеседование, разработчик указывает критерии начисления баллов и способы их фиксации в бланке. При отсутствии такой информации методика не может использоваться. Перевод (пересчет) «сырых баллов» в стандартизированные, является вторым этапом обработки результатов. Эта процедура позволяет сравнить результаты обследуемого с результатами других лиц, а также сопоставить несколько результатов, полученных разными методиками. Пересчёт сырых баллов в стандартизированные производится посредством специальной «конверсионной» таблицы. В ней, разработчик указывает способ соотнесения «сырых» и стандартизированных баллов. Важно соблюдать правила стандартизации, в том случае, если существует выбор показателей для нескольких групп обследуемых (мужчин, женщины, или разных возрастов). Следует выбрать показатели максимально приближенные к его половым, возрастным и культурным характеристикам. В практике работы психолог может использовать собственные стандартизированные показатели. Это является наиболее желательным, поскольку позволяет максимально полно учитывать специфику организации, вид деятельности и другие условия. Психологический смысл подобных норм в более точном отборе персонала. Для расчета подобных норм необходимо применять выборку, размером не менее 100 человек, соответствующих полу и возрасту обследуемых. Конечно, нормы могут рассчитываться в том числе и для стандартизированных анкет, бесед и прочих коммуникативных техник. Интерпретация результатов обследования. Этап и нтерпретации предполагает объяснение полученных результатов, построение выводов, диагноза и формулирование заключения. Основанием для интерпретации выступают результаты расчета стандартизированных баллов не только по отдельным шкалам, но их сочетаниям. В случае применения нескольких инструментов, интерпретация может обобщать их результаты. При интерпретации результатов обследования используются два основных подхода – клинический и статистический. Их сопоставление проводится в таблице 4.
Таблица 4
Сопоставление клинического и статистического подходов
Сопоставление подходов показывает, что клинический подход опирается на профессиональный опыт специалиста, статистический зависит от объективной, количественной информации об проявлениях исследуемого психологического явления. Прогностическая ценность клинического подхода определяется способностью к анализу опыта, интуиции и креативности специалиста диагноста. В противовес ему, прогнозирование в статистическом подходе опирается на математические модели регрессионного и детерминационного анализа. Можно говорить об эффективности клинического и статистического прогноза в их разумном сочетании. Поскольку, в целом, точность и надежность статистического подхода выше, чем клинического его применение должно использоваться в отношении типичных ситуаций. Клинический подход более эффективен по отношению к нетипичным ситуациям, дефиците диагностической информации, необходимой для принятия решения. Кроме того, клинический подход применив ситуации комплексного описания психологического явления, определении причин и факторов возникновения проблемы. Наконец, в исследовании качественными методами – например – наблюдении, беседы, проективной диагностике, качественной оценке процессов мышления клинический подход в интерпретации результатов является основным. Можно заключить, что оптимальным будет является сочетание статистического и клинического подходов, а не их противопоставление. Так, при интерпретации результатов сочетание подходов может обеспечиваться следующим образом. Статистический подход предполагает определение уровня полученных результатов на основе сопоставления с данными других обследований. Для этого могут использоваться следующие приемы: 1) качественный, предполагающий сравнение результатов без применения каких-либо статистических методов; 2) расчёт интегрального показателя по всей совокупности методик и определение полученного ранга в целом; 3) разработка профиля обследуемого и сопоставление его с «идеальным» профилем, разработанным на основе экспертных оценок; 4) сравнение результатов обследуемого с предварительно распределенными на группы результатами тестирования прошлых лет. Клинический подход применим при дополнении выводов, полученных от статистического анализа посредством сопряжения с другими источниками информации об обследуемом. В частности, результаты оценки можно сопоставить с нормативными данными, экспертными оценками руководителей, других сотрудников, специалистов по оценке и т.п. Подготовка заключения. Завершающий этап психодиагностического обследования предполагает построение диагностических заключений. Выделяются три способа подготовки заключений: симптоматический, этиологический, типологический. Симптоматическое заключение фиксирует полученные опрошенным результатов в терминах соответствия/отклонений. Например, делается вывод о соответствии уровня интеллекта нормативным показателям, типа характера определенному описанию и пр. Такой вид заключения не содержит аналитической и прогнозной части и, как правило, используется при проведении массовых обследований, на предмет наличия определенного явления, выраженности определенного состояния и пр. К, примеру, диагностика социально-психологического климата может сводится к заключении о благоприятном климате без дальнейшей детализации. Этиологическое заключение предполагает объяснение причин явления. Например, установив снижение климата в подразделении, исследователь формулирует предположение о возможных причинах этого явления, опираясь на механизм его измерения. При использовании методики социометрия, вывод о неблагоприятном климате может быть сделан из-за отсутствия взаимных выборов участников коллектива. Убедившись в этом, психолог может выдвинуть предположение об отсутствии взаимных выборов как вероятной причине нарушений климата. Рассуждая дальше, специалист предлагает программу коррекционных действий, которая повлияет на взаимопонимание и повысит частоту взаимных выборов. Таким образом, этиологическое заключение оценивает причины диагностированного уровня или состояния психологического явления, при этом оно опирается на закономерности измерения или выявленные факты. Специалист рассматривает эти закономерности или факты в качестве «мишеней» для своего преобразующего воздействия. Третий вид заключения – типологический является наиболее глубоким и комплексным. Здесь специалист отходит от описания причин в сторону типических проявлений данного явления. Например, считая, что неблагоприятный климат в подразделении может влиять на другие показатели совместной деятельности, состояние и самочувствие его участников. Таким образом, психодиагност переходит к оценке влияния полученных результатов на связанные с ними психологические явления. В данном случае заключение специалиста завершается разработкой программы психокоррекционных действий, выходящих за пределы нарушений конкретных параметров, и охватывающих субъекта, подвергшегося диагностике. Оформление заключения. При подготовке заключения специалист должен определить перечень включаемой в него информации. Типичная информация предполагает описание следующих параметров обследования: даты и времени, цели обследования; методов и методик, способах обработки (количественный, качественный анализ), информацию о решениях в однозначной формулировке (при проведении обследования на пригодность - «пригоден / не пригоден»); информацию о возможностях и ограничениях использования результатов тестирования. Итоги диагностического исследования должны быть представлены в общеупотребимых а не специальных терминах и понятиях. Представляются не, результаты диагностики посредством методик исследования, а их комплексная психологическая интерпретация. В практике тестирования персонала существует два типа выводов, относящихся к двум основным этапам интерпретации. Выводы первого типа основываются на общем представлении о терминологии оценивания, знании психологических явлений и, фактически отражают результаты проведенного исследования. Например: «обладает высоким уровнем интеллекта», «не имеет выраженных лидерских качеств», «мотивация к успеху – средняя». Выводы второго типа основываются на клиническом подходе к интерпретации результатов обследования. Они опираются опыт и компетентность специалиста, знание закономерностей поведения обследуемых, получивших подобные характеристики. Например: «с обязанностями руководителя не справится из-за отсутствия способности к распределению задач между сотрудниками», «в деятельности водителя будет успешен, при условии отсутствия монотонных поездок», «в экстремальной ситуации будет допускать ошибки в учете информации от окружающих, опираться на собственные представления». К заключению могут приобщаться: – описания полученных результатов в виде профилей, показателей шкал, параметров и т.д. (с информацией о критериальных значениях); – содержательная интерпретация результатов в терминах психологических инструментов; – диаграммы и графики и другие формы визуализации; – выводы и рекомендации (например, индивидуальные и/или групповые экспертные заключения, письменные отчеты). Контрольные вопросы 1. Какие этапы психодиагностической процедуры являются основными? 2. Какие действия необходимо провести психологу, осуществляющему планирование диагностического исследования? 3. В каких целях осуществляется сбор диагностической информации? 4. Какую информацию должен получить диагност, наблюдая за опрашиваемым в ходе обследования? 5. В чем заключаются последствия низкой прогностической валидности методики? 6. С какой целью собираются L-, Q- и Т-данные? 7. Чем следует руководствоваться подбирая психодиагностического исследования? 8. Зачем проводится перевод «сырых» баллов в стандартизированные? 9. Какие приемы следует использовать, готовя текст заключения? 10. Чем отличаются типы выводов в психодиагностическом исследовании? Тип шкалы |
Мера связи | ||||||||||||||||||
| Переменная X | Переменная Y | |||||||||||||||||||
| Интервальная или отношений | Интервальная или отношений | Коэффициент Пирсона | ||||||||||||||||||
| Ранговая, интервальная или отношений | Ранговая, интервальная или отношений | Коэффициент Спирмена | ||||||||||||||||||
| Ранговая | Ранговая | Коэффициент Спирмена | ||||||||||||||||||
| Дихотомическая | Дихотомическая | j – коэффициент Кеттелла | ||||||||||||||||||
| Дихотомическая | Ранговая | Рангово-бисериальный | ||||||||||||||||||
| Дихотомическая | Интервальная или отношений | Бисериальный |
Расчет коэффициента корреляции по Пирсону нуждается в следующих допущениях:
1. Переменные для анализа должны быть представлены в интервальной шкале или шкале отношений.
2. Распределения полученных эмпирических данных должны быть близки к нормальному.
3. Число измерений для сопоставляемых переменных должно быть одинаковым.
Формула для расчета коэффициента корреляции по Пирсону выглядит следующим образом:
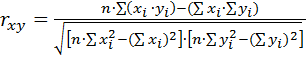 , ,
| (12) |
где х i – значения, принимаемые переменной X;
yi – значения, принимаемые переменной Y;
n – количество переменных.
Данная формула оптимальна при ручном (неавтоматизированном) расчете. Для дальнейшего упрощения можно построить следующую таблицу, заполнение которой способствует вычислению корреляционной связи. Полученные значения в графе «Сумма» табл. 5 необходимо подставить в формулу (12).
Таблица 5
Табличный расчет коэффициента корреляции по Пирсону
| № п/п | X | Y | X·X | Y·Y | X·Y |
| Сумма | Σ x | Σy | Σ x·x | Σ y·y | Σ x·y |
Величина коэффициента линейной корреляции находится в интервале: 1< r < + 1 и не может выходить за его пределы, т. е. равняться или превышать 1 по модулю. Интерпретация полученного коэффициента проводится на основе его фактического выражения по модулю полученного знака и уровня статистической значимости. Коэффициент корреляции, близкий к 1 по модулю, свидетельствует о высоком уровне связи между анализируемыми переменными, близкий к 0 – о низком уровне связи или ее отсутствии на данной выборке.
Знак корреляционной связи описывает характер зависимости. Положительный знак указывает на прямо пропорциональную зависимость, отрицательный – на обратно пропорциональную. То есть в первом случае с изменением одной переменной с определенной долей статистической вероятности можно говорить о последовательном изменении второй (согласованном росте или убывании), во втором случае с уменьшением одной переменной вторая увеличивается (и наоборот).
Заключительным этапом при расчете коэффициента корреляции является определение уровня статистической значимости полученной связи. С этой целью результаты вычислений по формуле (12) сопоставляются с табл. I в прил. 2. В данной таблице представлены критические значения коэффициентов корреляции по Пирсону для выборок от 4 до 1000 элементов (n).
Помимо установления связи между переменными, достаточно часто в психологических исследованиях ставится задача определения различий в выраженности какого-либо признака в связи с влиянием некоторых факторов. С этой целью применяется параметрический критерий t, иначе называемый критерий Стьюдента. Критерий Стьюдента был разработан английским химиком У. Госсетом в ходе работы на пивоваренном заводе Гиннеса. Поскольку по условиям контракта Госсет не имел права открытой публикации своих исследований, поэтому статьи по t-критерию были напечатаны в 1908 г. в журнале «Биометрика» под псевдонимом «Student». В отечественной литературе принято писать «Стьюдент»[56].
Простота вычисления t-критерия Стьюдента, а также его наличие в большинстве статистических пакетов и программ привели к широкому использованию этого критерия даже в тех условиях, когда применять его нельзя. Рассмотрим более подробно особенности использования статистического t-критерия Стьюдента.
Наиболее часто t-критерий используется в двух случаях. В первом случае его применяют для проверки гипотезы о равенстве генеральных средних двух независимых, несвязанных выборок (так называемый двухвыборочный t-критерий). В этом случае есть контрольная и опытная группы, состоящие из разных лиц, их количество в группах может быть различно. Во втором же случае используется так называемый парный t-критерий, когда одна и та же группа объектов порождает числовой материал для проверки гипотез о средних. Поэтому эти выборки называют зависимыми, связанными. Например, психологические свойства одних и тех же лиц до и после психологического тренинга. В обоих случаях должно выполняться требование нормальности распределения исследуемого признака в каждой из сравниваемых групп.
Следующее требование, которое должно выполняться, – это равенство дисперсий в сравниваемых группах. Чем больше различаются между собой дисперсии и объемы выборок, тем сильнее отличается распределение «вычисляемого t-критерия» от распределения истинного «t-критерия Стьюдента». При этом различную величину имеют и сам t-критерий, и такой параметр этих распределений, как число степеней свободы.
В свою очередь, число степеней свободы сказывается на величине достигнутого уровня значимости (р <...), определяемого для вычисленной величины t-критерия. Во многих статистических пакетах величина t-критерия вычисляется для двух случаев: 1) дисперсии равны, 2) дисперсии не равны. При этом предполагается, что в обоих случаях требование нормальности распределения выполняется.
Таким образом, для принятия решения о применении t-критерия Стьюдента к данным следует придерживаться таких критериев:
1. Данные должны быть представлены в шкале интервалов либо отношений.
2. Сравниваемые выборки должны иметь распределение, близкое к нормальному.
3. Сравниваемые выборки должны иметь одинаковый размер.
Формула t-критерия Стьюдента имеет следующий вид:
для несвязанных выборок:
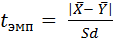 , ,
| (13) |
и
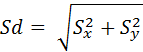 , ,
| (14) |
где
Х – среднее арифметическое для X;
Y – среднее арифметическое для Y;
Sd – сумма среднеквадратических отклонений X и Y.
Число степеней свободы вычисляется для неравных групп: k = n1 + n2 – 2, где n1 – выборка первой группы, n2 – второй; для равных по размеру групп:
k = 2 · n – 2, где n – объем выборки;
для связанных выборок:
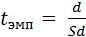 0, 0,
| (15) |
где
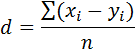
| (16) |
и
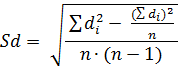
| (17) |
Число степеней свободы вычисляется как k = n – 1, где n – объем выборки. t-критерий Стьюдента без применения пакета статистических программ может быть рассчитан «вручную». С этой целью необходимо заполнить табл. 6. Приведем пример для несвязанных выборок.
Таблица 6
Табличный расчет t-критерия Стьюдента для несвязанных выборок
| № п/п |
Значения по группам |
Отклонения от среднего |
Квадраты отклонений | |||
| X | Y | 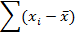
| 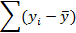
| 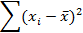
| 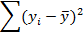
| |
| 1 | ||||||
| Сумма | Σ x | Σy | 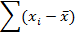
| 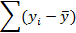
| 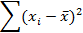
| 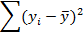
|
| Среднее | 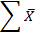
| 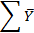
| ||||
Полученные в таблице значения подставляются в формулы (13) и (14).
Непараметрические процедуры математико-статистического анализа. В качестве непараметрического метода изучения корреляционных связей в выборке можно применять коэффициент ранговой корреляции Спирмена. Этот коэффициент определяет степень тесноты связи порядковых признаков, которые представлены в виде рангов сравниваемых величин.
Величина данного коэффициента ранговой корреляции лежит в интервале от –1 до +1. Как и линейный коэффициент Пирсона, может принимать положительные и отрицательные значения, характеризуя, в то же время, направленность связи между признаками, представленными в ранговой шкале.
Расчет коэффициента ранговой корреляции предполагает соблюдение ряда требований:
1. Сравниваемые переменные должны быть представлены в ранговой шкале.
2. Число сопоставляемых признаков должно быть одинаковым.
Формула расчета коэффициента корреляции по Спирмену при отсутствии в выборке одинаковых рангов выглядит следующим образом:
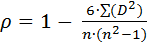 , ,
| (18) |
где
n – объем выборки (количество ранжируемых признаков);
D – разность между рангами по двум переменным для каждого испытуемого;
∑(D 2) – сумма квадратов разностей рангов.
В случае если в выборке находятся одинаковые ранги, в формулу вычисления коэффициентов корреляции добавляются поправки на одинаковые ранги. Изменения претерпевает числитель формулы (18). В случае, если в первой сопоставляемой группе присутствуют одинаковые ранги, в числитель необходимо добавить следующий коэффициент (D1):
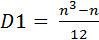 , ,
| (19) |
где n – число одинаковых рангов.
Таким образом, формула (18) модифицируется до:
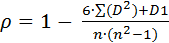 , ,
| (20) |
После вычисления эмпирического значения ρ полученный коэффициент сопоставляется с табличным. Отметим, что табличные значения при расчете коэффициента ранговой корреляции Стьюдента от n = 5 до n = 40 представлены в табл. III прил. 2, при n > 40 справедливы критические значения коэффициента линейной корреляции по Пирсону (табл. IV прил. 2).
Критерий хи-квадрат (х2) распределения используется для расчета согласия эмпирического распределения теоретическому, а также для расчета однородности экспериментальных выборок. При совпадении эмпирического и теоретического распределения величина х2ЭМП = 0, с увеличением этих значений расхождение также увеличивается.
Формула х2:
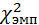 = = 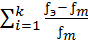 , ,
| (21) |
где
f Э = эмпирическая частота;
fm = теоретическая частота;
k = количество разрядов признака.
Для сравнения двух эмпирических распределений (в зависимости от вида представленных данных) формула для расчета х2 распределения может иметь вид:
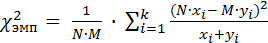 , ,
| (22) |
где N и M – количество элементов в сопоставляемых выборках.
Для расчета уровня значимости х2 распределения используется понятие степени свободы, которое рассчитывается по формуле: v = k – 1, где k – количество элементов в выборке. Таблица критических значений приведена в табл. IV прил. 2.
Непараметрическим критерием, предназначенным для сравнения независимых выборок, аналогичным t-критерию Стьюдента, является U-критерий Манна – Уитни:
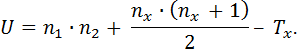
| (23) |
Этот критерий не требует проверки на нормальность распределения, с его помощью можно сравнивать маленькие выборки объемом от 3 наблюдений. Также он подходит для сравнения выборок, данные в которых распределены ненормально.
Алгоритм расчета следующий:
1. Составить единый ранжированный ряд из обеих сопоставляемых выборок, расставив их элементы по степени нарастания признака и приписав меньшему значению меньший ранг. Общее количество рангов получится равным:
N = n1 + n2,
где n1 – количество единиц в первой выборке;
n2 – количество единиц во второй выборке.
2. Разделить единый ранжированный ряд на два, состоящие, соответственно, из единиц первой и второй выборок. Подсчитать отдельно сумму рангов, пришедшихся на долю элементов первой выборки, и отдельно – на долю элементов второй выборки. Определить большую из двух ранговых сумм (Tx), соответствующую выборке с nx единиц.
3. Определить значение U-критерия Манна – Уитни по формуле (23).
По таблице для избранного уровня статистической значимости определить критическое значение критерия для данных n1 и n2. Если полученное значение U меньше табличного или равно ему, то признается наличие существенного различия между уровнем признака в рассматриваемых выборках (принимается альтернативная гипотеза). Если же полученное значение U больше табличного, принимается нулевая гипотеза. Достоверность различий тем выше, чем меньше значение U.
При справедливости нулевой гипотезы критерий имеет математическое ожидание 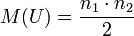 и дисперсию
и дисперсию 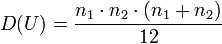 и при достаточно большом объеме выборочных данных
и при достаточно большом объеме выборочных данных 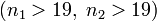 распределен практически нормально.
распределен практически нормально.
Коэффициент ассоциации φ используется для определения отношения между переменными, представленными в дихотомической шкале. Величина коэффициента φ лежит в интервале от –1 до 1, соответственно, он может принимать положительные и отрицательные значения, свидетельствуя о характере связи между дихотомическими переменными.
В общем виде формула вычисления коэффициента φ выглядит так:
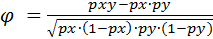 , ,
| (24) |
где px – частота признака, имеющего 1 по x;
py – частота признака, имеющего 1 по y;
(1 – px) – частота признака, имеющего 0 по x;
(1 – py) – частота признака, имеющего 0 по y;
pxy – частота признака, имеющего 0 по x и 0 по y одновременно.
Применение данного коэффициента корреляции должно сопровождаться определением критических значений, для расчета которых применяется формула t-критерия Стьюдента:
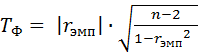 , ,
| (25) |
где r ЭМП – коэффициент корреляции, n – число коррелируемых признаков, а уровень значимости ТФ определяется по табл. II прил. 2, причем k = n – 2.
Коэффициент сопряженности Пирсона. Помимо коэффициента ассоциации, при проведении расчетов в случаях, когда обе переменные представляют собой дихотомическую шкалу, можно использовать коэффициент четырехклеточной сопряженности Пирсона:
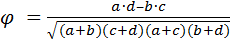 , ,
| (26) |
Классификация объектов по дихотомической шкале приведет к построению четырехклеточной таблицы. К примеру, курсант может посетить более 50 % тренировок, а может и не посетить, может сдать зачет с первого раза, а может и не сдать. Данные для расчетов заносятся в таблицу (см. табл.7).
Таблица 7
Таблица четырехклеточной классификации
| Показатель | Сдал зачет с первого раза | Не сдал зачет с первого раза |
| Курсант посещал тренировки | a | b |
| Курсант не посещал тренировки | c | d |
В клетки a, b, c, d таблицы следует вписать количество объектов, обладающих соответствующими признаками. Приведенный коэффициент является модификацией коэффициента корреляции Пирсона, и расчет критических значений коэффициента сопряженности может быть произведен с помощью критических значений для коэффициента Пирсона, представленных в прил. 2.
Рангово-биссериальный коэффициент корреляции. Данный коэффициент применяется в случае, когда одна переменная измерена в дихотомической шкале, а другая – в ранговой. Особенностью данного коэффициента является то, что его знак, полученный на интервале от +1 до –1 не имеет никакого значения для интерпретации.
Расчет коэффициента рангово-биссериальной корреляции Rrb производится по формуле:
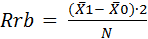 , ,
| (27) |
где
Х1 – средний ранг по элементам переменной Y, которым соответствует признак 1 в переменной X;
Х0 – средний ранг по элементам переменной Y, которым соответствует признак 0 в переменной Y;
N – общее количество элементов в переменной X.
Оценка уровня значимости коэффициента Rrb проводится по уже известной формуле (25).
Точечно-биссериальный коэффициент корреляции. Данный коэффициент корреляции применяется в тех случаях, когда одна переменная представлена в биссериальной шкале, а вторая – в шкале интервалов или отношений. Коэффициент может принимать значения от –1 до 1, но, как и в случае рангово-биссериальной корреляции, его знак не интерпретируется.
Для расчета коэффициента применяется формула:
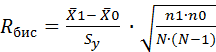 , ,
| (28) |
где
Х1 – среднее по тем элементам переменной Y, которым соответствует код 1 в переменной X. Тогда n 1 – количество 1 в переменной X;
Х0 – среднее по тем элементам переменной Y, которым соответс
|
| Поделиться: |




