
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Preparation of modern pedagogical personnelСодержание книги
Поиск на нашем сайте
Abstract. The article describes the role of studying methods of solving linear programming problems in the preparation of future mathematics teachers. The table is given with the significant advantages and disadvantages of the two linear programming methods. An example of solving the linear programming problem by the simplex method is given. Keywords: teacher training, linear programming, optimal solution, simplex method.
В век непрерывного совершенствования современных технологий немаловажную роль для человека играют его умения быстро находить правильные решения на ряд глобальных проблем современности и выбирать наиболее эффективные способы решения задач различного характера. Решение многих как математических, так и прикладных задач основывается на построении моделей. Например, одним из способов решения задач, сводимых к системе линейных уравнений или неравенств, является линейное программирование (ЛП). Для задач ЛП существуют свои определённые методы решения [1; 2; 3] и соответствующая математическая база (обеспечение) для различных ситуаций. Наибольшую известность получили два метода решения задач линейного программирования (ЗЛП) – это графический (иногда его называют геометрическим) и симплексный (симплекс-метод) методы. От умения осуществлять выбор между методами решения ЗЛП зависит не только скорость принятия оптимального решения, но и точность принимаемого решения. Охарактеризуем каждый из двух методов и составим таблицу с результатами сравнения этих методов относительно основных характеристик. Широко распространённым, наиболее простым и наглядным является графический метод. Данным методом решаются задачи, как правило, имеющие либо две переменные, либо более двух переменных, но при условии, что в канонической записи задачи содержится не более двух свободных переменных. Графический способ решения ЗЛП предполагает несколько этапов [2]: 1) построение пространства допустимых решений, которые удовлетворяют всем ограничениям модели; 2) нахождение оптимального решения среди всех точек пространства допустимых решений. Техника графического решения задачи линейного программирования позволяет выявить многие свойства оптимального решения ЛП [3]. Существенным недостатком симплекс-метода является необходимость пересчета всех коэффициентов и свободных членов полной системы уравнений. Эта необходимость обусловлена тем, что формулы симплекс-метода предусматривают вычисление всех искомых коэффициентов, что, в свою очередь, значительно увеличивает объем расчетов и замедляет отыскание оптимального решения. Однако, симплекс-метод, в отличие от графического метода, является наиболее универсальным в решении ЗЛП. Указанные выше характеристики графического и симплексного методов решения задач ЛП можно представить в виде следующей таблицы (см. табл. 1) [1; 2; 3]. Таблица 1 Преимущества и недостатки графического и симплексного Методов решения ЗЛП
Итак, каждый из методов имеет как достоинства, так и недостатки, но наиболее наглядным методом решения ЗЛП является графический метод, а наиболее точным в вычислениях – симплексный. Так при решении ЗЛП для начала следует определить число неизвестных, привести задачу к каноническому виду (добавить дополнительные переменные для перехода из системы неравенств к системе уравнений). Если число неизвестных не превышает двух, то решить задачу графическим способом, иначе – симплексным. Рассмотрим следующую задачу и решим её, сопоставив характеристики методов решения и условие данной задачи: «Строительная компания производит полки для ванных комнат двух размер – A и B. Агенты по продаже считают, что на рынке может быть реализовано до 500 полок в неделю. Для каждой полки типа A требуется 2 Для решения данной задачи, в первую очередь, необходимо составить математическую модель. В задаче за неизвестные возьмем две переменные. Поскольку задача носит практический характер и необходимо наиболее точно определить значения неизвестных, то решение будем проводить, используя симплексные таблицы, то есть симплекс-методом. Пусть То есть задача линейного программирования будет иметь вид Для решения задачи симплексным методом введем три дополнительные переменные В качестве опорного плана выберем Таблица 2 Начальная симплексная таблица
Поскольку последняя оценочная строка содержит отрицательные оценки, тогда выберем разрешающий столбец, то есть столбец с наименьшей оценкой, а затем по наименьшему отношению свободных членов к коэффициентам этого столбца найдём разрешающий элемент (разрешающий элемент будем выделять жирным). Результат запишем в новую таблицу (см. табл. 2). Аналогично будем повторять данные шаги, пока не придём к таблице с неотрицательными оценками (см. табл. 3 и табл. 4). Таблица 3 Вторая симплексная таблица
Таблица 4 Третья симплексная таблица
В последнем плане строка оценок не содержит отрицательных значений, поэтому план Рассмотренная теория изучается студентами математического факультета Пермского государственного гуманитарно-педагогического университета в рамках курса по выбору «Исследование операций». Вышеуказанная характеристика методов решения ЗЛП позволяет констатировать значимую роль их изучения в подготовке будущих учителей математики, в частности, заключающуюся в развитии логического мышления, формирования у обучающихся системы профессиональных компетенций через овладение ими математическим языком и математической символикой. Список литературы 1. Аксентьев В.А. Методы оптимальных решений: учебное пособие / В.А. Аксентьев. – Тюмень: ТГУ, 2013. – 452 2. Губарь Ю.В. Введение в математическое программирование Ю.В. Губарь. – М.: ИНТУИТ, 2016. – 226 c. 3. Семериков А.В. Решение задач линейного программирования с использованием симплекс метода: Методические указания для выполнения практических работ / А.В. Семериков. – Ухта: УГТУ, 2007. – 52 с. УДК 343 Льянова Светлана Ахметовна, Кандидат экономических наук, доцент, Ингушский государственный университет, г. Магас, РФ Соломонова Ханум Акиваевна, Куратор по эмигрантам Министерство образования Израиля г. Акко, Израиль
ЗАКОНОДАТЕЛЬНЫЕ ТРЕБОВАНИЯ К СЛУЖЕБНОМУ ПОВЕДЕНИЮ Аннотация: Требования к служебному поведению должны определять систему нравственных стандартов, конкретных норм поведения гражданских служащих при реализации полномочий государственных органов. Требования определяют в том числе и этические нормы служебного поведения. Мораль гражданского служащего не может основываться только на собственном представлении о нравственности, она определяется и общественными потребностями. Ключевые слова: поведение, мораль, нравственность, этика.
Lyanova Svetlana Ahmetovna, Candidate of Economics, Associated Professor, Ingush State University, Magas, Russian Federation Solomonova Hanum Akivaevna, Emigrant Curator, Israeli Ministry of Education, Acre, Israel
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2019-12-25; просмотров: 143; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.18.59 (0.011 с.) |

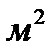 материала, а для полки типа B – 4
материала, а для полки типа B – 4  . Компания может получить до 1300
. Компания может получить до 1300  материала в неделю. Для того чтобы изготовить одну полку типа A требуется 13 минут машинного времени, а для того, чтобы изготовить одну полку типа B – 30 минут; машину в неделю можно использовать лишь 165 часов. Определить количество полок каждого типа, которые следует выпускать в неделю, если прибыль от продажи полок типа A составляет 4 денежных единицы, а от полок типа B – 5 денежных единиц».
материала в неделю. Для того чтобы изготовить одну полку типа A требуется 13 минут машинного времени, а для того, чтобы изготовить одну полку типа B – 30 минут; машину в неделю можно использовать лишь 165 часов. Определить количество полок каждого типа, которые следует выпускать в неделю, если прибыль от продажи полок типа A составляет 4 денежных единицы, а от полок типа B – 5 денежных единиц».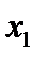 – количество полок вида A,
– количество полок вида A,  – количество полок вида B, которые производятся в неделю (по смыслу задачи эти переменные неотрицательны). Прибыль от продажи такого количества полок составит
– количество полок вида B, которые производятся в неделю (по смыслу задачи эти переменные неотрицательны). Прибыль от продажи такого количества полок составит 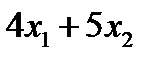 , при условии, что прибыль требуется максимизировать. Далее следует выписать систему ограничений к задаче. Так как в неделю на рынке может быть реализовано до 500 полок, отсюда имеем неравенство
, при условии, что прибыль требуется максимизировать. Далее следует выписать систему ограничений к задаче. Так как в неделю на рынке может быть реализовано до 500 полок, отсюда имеем неравенство 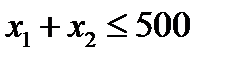 . Затраты материала могут быть представлены в виде неравенства
. Затраты материала могут быть представлены в виде неравенства  . Затраты машинного времени можно представить неравенством
. Затраты машинного времени можно представить неравенством  .
. с соответствующей системой ограничений, которая имеет вид
с соответствующей системой ограничений, которая имеет вид 
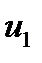 ,
,  ,
, 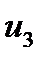 и приведём её к каноническому виду, то есть
и приведём её к каноническому виду, то есть  ,
, 
 и составим начальную симплекс-таблицу (см. табл. 2):
и составим начальную симплекс-таблицу (см. табл. 2):
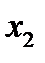
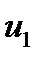




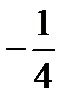










 ,
,  оптимален, целевая функция принимает значение 2150. То есть для получения максимальной прибыли, предприятию можно производить лишь 350 полок вида A и 150 полок вида B, тогда прибыль составит 2150 денежных единиц, при этом неиспользованными останутся 850 минут (14 полных часов) машинного времени.
оптимален, целевая функция принимает значение 2150. То есть для получения максимальной прибыли, предприятию можно производить лишь 350 полок вида A и 150 полок вида B, тогда прибыль составит 2150 денежных единиц, при этом неиспользованными останутся 850 минут (14 полных часов) машинного времени.


