
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет на прочность червячных передачСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте В червячных передачах, аналогично зубчатым, зубья червячного колеса рассчитывают на контактную прочность и прочность при изгибе. Как отмечалось выше (см. § 18.8), в червячных передачах кроме выкрашивания рабочих поверхностей зубьев велика опасность заедания, которое также зависит от величины контактных напряжений он. Поэтому для всех червячных передач расчет по контактным напряжениям является основным, определяющим размеры передачи, а расчет по напряжениям изгиба — проверочным. Расчет по контактным напряжениям. В основу вывода расчетной формулы для червячных передач положены те же исходные зависимости и допущения, что и при рассмотрении зубчатых передач (см. § 13.4). Вывод формулы ведут для передачи с архимедовым червяком, у которой условия зацепления и несущая способность мало отличаются от других передач с линейчатыми червяками. Наибольшее контактное напряжение в зоне зацепления по формуле Герца (2.13)
где Е1 и Е2 v1 и v2 — соответственно модули упругости и коэффициенты Пуассона стального червяка и бронзового или чугунного венца колеса (см. § 5.2); w — нормальная нагрузка на единицу длины контактной линии. Эта нагрузка распределена неравномерно вследствие деформаций валов червяка и колеса, а также подшипников и корпуса передачи:
Здесь Fn — сила, нормальная к поверхности зуба червячного колеса и витка червяка и приложенная в полюсе зацепления. Согласно рис. 18.10, а Fn= FJ(cos a cosψK); l Σ — суммарная длина контактных линий в зацеплении червячной передачи. Согласно рис. 18.11 длина одной контактной линии прямо пропорциональна начальному диаметру червяка dwl и углу обхвата 28. Если учесть, что с увеличением угла ψк подъема витка длина линии контакта растет обратно пропорционально cos ψкто при коэффициенте εа перекрытия и минималь- ном значении коэффициента ξ, колебания суммарной длины контактных линий получим
При средних значениях коэффициента ξ = 0,75, угла обхвата 2δ= 100° и коэффициента торцового перекрытия в средней плоскости сечения колеса εα = 2 суммарная длина контактных линий После подстановки получим
Здесь дополнительно введен коэффициент нагрузки КΗ = КΗβ КΗν учитывающий неравномерность распределения нагрузки в зоне контакта вследствие деформации деталей передачи (KHβ), а также внутренней динамики передачи (КΗν). рпр — приведенный радиус кривизны профилей витков червяка и зубьев колеса в полюсе зацепления. В осевом сечении профиль витка архимедова червяка прямолинейный (p1=°°, см. рис. 18.6), а зубья червячного колеса имеют эвольвен-гный профиль, поэтому приведенный радиус кривизны для червячной пары равен радиусу кривизны профиля зуба червячного колеса в полюсе зацепления (см. § 13.4):
Подставив значения Е, v, w, рпр в формулу Герца и приняв а = 20°, ψw. = 10°, а также заменив значения Ft2 = 2- 103 T2/ d2; d2 = mz2, dw1 = m{q + 2x); m = 2aw /(z2 + q + 2x), получим формулу проверочного расчета червячных передач по контактным напряжениям:
(18.28) где σΗ—расчетное контактное напряжение в зоне зацепления, Н/мм2; аw — межосевое расстояние, мм; Т2 — вращающий момент на колесе, Н • м. Значения коэффициента Za для червячных передач:
Червячные передачи с нелинейчатыми червяками имеют более благоприятное соотношение радиусов кривизны червяка и колеса, боль-тую суммарную длину контактных линий, что обусловливает их повышенную нагрузочную способность. Червячные передачи работают плавно, бесшумно, поэтому в них пополнительные динамические нагрузки невелики. Хорошая приработка зубьев колес к виткам червяков значительно уменьшает концентрацию нагрузки. При обычной точности изготовления и выполнении условия жесткости червяка [см. формулу (18.34)] принимают: Кн= 1 при v2<3 м/с; Кн= 1,1...1,3 при v2 > 3 м/с, где v2 —окружная скорость червячного колеса. Приняв из условия жесткости червяка q = Q,25z2, а также К„=1, х = 0 и решив зависимость (18.28) относительно а„, получим формулу проектировочного расчета червячных передач:
где аи, — межосевое расстояние, мм; [σ]Η—в Н/мм2; Т2 — в Нм. Значения коэффициента Ка для червячных передач:
Полученное расчетом значение aw округляют в большую сторону до стандартного значения (см. § 18.4) или до ближайшего значения из ряда нормальных линейных размеров (см. § 27.4). Расчет по напряжениям изгиба. Расчет зубьев червячного колеса на изгиб аналогичен расчету зубьев цилиндрических косозубых колес. В формулу (13.14) вводят поправки, связанные с выражением входящих в нее величин через параметры червячной передачи и учитывающие более высокую прочность зубьев червячного колеса на изгиб (на - 30 %) вследствие их дугообразной формы (см. рис. 18.11). С учетом этих поправок при KF= Кн получают формулу проверочного расчета зубьев червячного колеса по напряжениям изгиба:
КПД червячных передач Роль смазывания в червячной передаче еще важнее, чем в зубчатой, так как в зацеплении происходит скольжение витков червяка вдоль контактных линий зубьев червячного колеса. В случае несовершенства смазывания резко возрастают потери, возможно повреждение зубьев. Червячная передача является зубчато-винтовой и имеет потери, присущие как зубчатой передаче, так и передаче винт — гайка. В общем случае КПД червячной передачи
где ηп, ηзв и ηрм — КПД, учитывающие потери соответственно в подшипниках, зубчато-винтовой паре, а также на размешивание и разбрызгивание масла. Практически КПД червячной передачи определяют по формуле (6.8), полученной для винтовой пары:
(18.32) Значения угла φ' трения в зависимости от скорости скольжения приведены в табл. 18.4. Они получены экспериментально для червячных передач на опорах с подшипниками качения, т. е. в этих значениях учтены потери мощности в подшипниках качения, в зубчатом зацеплении и на размешивание и разбрызгивание масла. Величина φ' значительно снижается при увеличении vs, так как при больших скоростях в зоне контакта создаются благоприятные условия для образования масляного слоя, разделяющего витки червяка и зубья колеса и уменьшающего потери в зацеплении. Таблица 18.4. Значения угла φ' трения в червячной передаче при различных скоростях v, скольжения
Примечание. Меньшие значения φ' для передач с венцом колеса из оловянной бронзы, большие — из безоловянной бронзы и чугуна. Из формулы (18.32) следует, что с увеличением ψw растет КПД передачи. Полагая для простоты х=0 [см. формулу (18.8)], получаем tg ψw = z1 / qОтсюда следует, что увеличение q, и уменьшение q в допустимых пределах обеспечивают повышение КПД червячной передачи. Червячные передачи имеют сравнительно низкий КПД, что ограничивает область их применения (ц = 0,75...0,92). Рекомендации по расчету на прочность Расчет червячных передач на прочность ведут в последовательности, изложенной в решении примера 18.1. При этом: а) модуль зацепления определяют по формуле
Для силовых передан принимают q = (0,22...0,4)г2; в) коэффициент х смещения режущего инструмента должен быть г) при определении расчетного контактного напряжения допуска Тепловой расчет При работе червячных передач вследствие их невысокого КПД выделяется большое количество теплоты. Мощность (1-ц)Ри потерянная на трение в зацеплении и подшипниках, а также на размешивание и разбрызгивание масла, переходит в теплоту, нагревая масло, детали передачи и стенки корпуса, через которые она отводится в окружающую среду. Если отвод теплоты недостаточен, то передача может перегреться. При перегреве резко уменьшается вязкость масла и возникает опасность заедания, что может привести к выходу передачи из строя. Тепловой расчет червячной передачи при установившемся режиме работы производят на основе теплового баланса, т. е. равенства тепловыделения Q„ и теплоотдачи Qa. Тепловой поток, Вт (тепловая мощность), передачи в одну секунду
Здесь Тг — в Нм; п2 — в мин"'. Тепловой поток, Вт (мощность теплоотдачи), наружной поверхности корпуса редуктора в одну секунду
где А — площадь только той части поверхности корпуса, которая омывается внутри маслом или его брызгами, а снаружи воздухом, м\ Поверхность днища корпуса не учитывают, так как она не омывается свободно циркулирующим воздухом. Приближенно поверхность А охлаждения корпуса можно принимать в зависимости от межосевого расстояния:
λ — коэффициент, учитывающий отвод тепла от днища редуктора в основание. При установке редуктора на металлической плите или раме λ = 0,1...0,3 (в зависимости от прилегания корпуса к плите); на бетонном или кирпичном основании λ-0; tB — температура воздуха снаружи корпуса (в условиях цеха обычно tB = 20° С); tм — температура масла в корпусе передачи, °С; Кт — коэффициент теплопередачи, характеризующий тепловой поток, передаваемый в секунду одним квадратным метром поверхности корпуса при перепаде температур в один градус (зависит от материала корпуса редуктора и скорости циркуляции воздуха — интенсивности вентиляции помещения). Для чугунных корпусов при естественном охлаждении КТ = 13...18 Вт/(м2 ■ °С). Большие значения принимают при незначительной шероховатости и чистых поверхностях наружных стенок, хорошей циркуляции воздуха вокруг корпуса и интенсивном перемешивании масла (при нижнем расположении червяка). По условию теплового баланса Qn = Q0, т. е.
откуда температура масла в корпусе червячной передачи при непрерывной работе без искусственного охлаждения Значение [t]M зависит от марки масла: [f]M = 95...110° С. Если при расчете получают tM>[t]M, то необходимо увеличить поверхность охлаждения А, предусмотрев охлаждающие ребра. Ребра
располагают вертикально по направлению движения свободно циркулирующего воздуха. В расчете учитывают только 50 % поверхности ребер в связи с теплообменом между соседними ребрами. Можно применять искусственное охлаждение, например, обдувом корпуса воздухом с помощью вентилятора, насаженного на вал червяка (рис. 18.12). В этом случае ребра располагают горизонтально — вдоль направления потока воздуха от вентилятора. В этом случае
Рис. 18.12. Охлаждение ребристого корпуса редуктора обдувом воздуха от вентилятора: / — охлаждающие ребра; 2— вентилятор
Коэффициент КТв теплоотдачи при обдуве вентилятором
В червячных передачах с большим тепловыделением применяют охлаждение масла водой, проходящей по змеевику (рис. 18.13, а), или применяют циркуляционную систему смазывания со специальным холодильником (рис. 18.13,6).
Рис. 18.13. Схемы искусственного охлаждения червячных передач: /—насос; 2-—фильтр; J —холодильник
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1318; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.009 с.) |



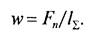

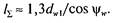
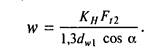














 (18.36)
(18.36)






