
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Схемы применения зубчатых передач.Содержание книги
Поиск на нашем сайте
Основным кинематическим параметром любой зубчатой передачи является общее передаточное отношение u:
где ui-j – передаточное число ступени передачи; k – число внешних зацеплений.
Рис. IX. 10
Множитель (-1) k позволяет определить направление вращения первого зубчатого колеса по отношению к последнему. Так, для одноступенчатого редуктора (Рис. IX. 10) общее передаточное отношение u определяется:
где k =1, тогда:
знак «-» показывает, что выходной вал этого редуктора вращается в противоположную сторону относительно входного колеса.
Рис. IX. 11
Аналогично рассчитывается общее передаточное отношение для рядной двухступенчатой передачи (Рис. IX. 11):
Колесо 2 не влияет на общее передаточное отношение. Такое колесо называется паразитом. На практике колеса-паразиты используются для изменения направления вращения выходного вала редуктора или для обеспечения нужных габаритов передачи.
а) б) Рис. IX. 12 Двухступенчатая передача (Рис. IX. 12, а) достаточно применима в механике и может использоваться с различными особенностями компоновки. В связи с габаритным разбросом более рациональным является использование соосной компоновки передачи (Рис. IX. 12, б):
Некоторые особенности наблюдаются в схемах компоновки передач с внутренним зацеплением (Рис. IX. 13).
Рис.IX. 13 Для таких передач множитель (-1) k не применим, т.к. здесь есть и внешние, и внутренние зацепления. В оборудовании химического производства большое применение имеют планетарные редукторы (Рис. IX. 14), главным достоинством которых является компактность при относительно больших передаточных отношениях и равномерность распределения нагрузки на все элементы передачи.
а) б) Рис. IX. 14 Неподвижное колесо 3 называется опорным, входная шестерня 1 – центральным (или солнечным) колесом, колесо 2 с подвижной осью – сателлит – имеет внешнее и внутреннее зацепление соответственно с центральным колесом 1 и неподвижным колесом 3, выходной вал вместе с корпусом подшипников промежуточного вала 2 называется водилом. Обкатываясь по центральному колесу 1, промежуточное колесо 2 увлекает за собой водило. Главной проблемой при проектировании планетарных передач является общее передаточное отношение uобщ:
В связи с числом зубьев этой планетарной передачи:
передаточное отношение u1,Н рассчитывается с использованием теоремы Виллиса. Принцип метода Виллиса заключается в мысленном вращении всего механизма со скоростью водилы в обратном направлении (метод обращенного движения), при этом водило останавливается, а неподвижное колесо 3 начинает вращаться:
и
Планетарная передача превращается в механизм обыкновенного ряда:
где k =1, тогда:
Сателлит 2 не влияет на общее передаточное отношение, т.е. является паразитным колесом, тогда в процессе проектирования мы можем назначить произвольное число зубьев z 2. Используя свойство угловой скорости ω как вектора, направленного по нормали к плоскости вращения, передаточное отношение u1,3 можно расписать как:
Тогда с учетом того, что колесо 3 передачи является неподвижным, т.е.:
получим:
Как правило, u1,Н задано или находится в процессе проектирования, тогда:
Для дальнейшего проектирования необходимо учесть условие зацепления:
и технологическое требование исходя из условий нарезания зубьев:
Червячные передачи. Червячные передачи (Рис. IX. 15) по сравнению с другими видами передач отличаются плавностью хода, бесшумностью работы, компактностью и большим передаточным отношением, в связи с чем имеют большое применение в промышленности.
Рис. IX. 15 Однако главной особенностью и недостатком передачи является наличие большого усилия трения между зубьями червяка и зубьями червяного колеса, что приводит к необходимости обильной смазки. Особым преимуществом червячных передач является эффект самоторможения, который заключается в том, что вращение возможно только от червяка к червячному колесу, обратного хода – нет. Червячные редукторы относятся к классу гиперболических передач, в основу которого заложено пересечение гиперболоидов (Рис. IX. 16).
а) б) Рис. IX. 16 В зоне контакта А1А2 стиль зацепления дает гипоидную передачу, в зоне В1В2 – дает винтовую передачу (или червячную), где зубья колеса и червяка нарезаются по винтовой линии (спирали). По конфигурации червяка червячные передачи делят на цилиндрические (Рис. IX. 17, а) и гипоидные (Рис. IX. 17, б).
а) б) Рис. IX. 17 Силовое взаимодействие червяка и колеса в зоне контакта у гипоидных передач больше, однако гипоидные передачи дороже в изготовлении. Профиль зуба червячных передач может быть трапециидальным. Недостатком таких передач является большие потери трения, поэтому чаще используют эвольвентный профиль зуба. Геометрия червячного зацепления связана с тем, что при зацеплении зубья червяка и червячного колеса вынуждены преодолевать силу трения (скольжения).
Рис. IX. 18 При вращении червяка возникают осевая υос и тангенциальная υt скорости, векторная сумма которых дает скорость скольжения υск (Рис. IX. 18), направленную по касательной к спирали нарезки червяка. При подъеме нарезки червяка под углом γ:
Скорость скольжения функционально связана с коэффициентом трения червячной передачи. Чем больше скорость скольжения (трения), тем больше угол трения ρ (коэффициент трения):
тогда расчетный КПД передачи определяется углом трения φ:
Реальные потери на трение в червячной паре рассчитываются через реальный КПД:
где u – передаточное отношение между червяком и червячным колесом, определяемое числом zч . спиралей (заходов), нарезанных на червяке, и числом zч.к. зубьев червячного колеса:
В связи с большими потерями на трение, КПД червячной передачи (η =0,7) значительно ниже КПД зубчатой передачи (η ≈0,95). Энергия, затрачиваемая на преодоление трения, необратимо переходит в тепловую. Поэтому червячные передачи требуют обильной смазки, уменьшающей трение и отводящей значительное количество тепла. Количество смазки определяется долей G тепловой энергии:
и рассчитывается по формуле:
где Gм – расход масла теплоемкостью См масла, понижающего температуру на ∆t.
Общие геометрические зубчатой пары червячной передачи не отличаются от зубчатого зацепления. Общими габаритными параметрами являются диаметр dωЧ окружности нарезки червяка (или делительной окружности), диаметр dаЧ окружности выступов и диаметр dfЧ окружности впадин (Рис. IX. 19).
Рис. IX. 19 Наряду с этим и для червячного колеса, и для червяка общим геометрическим параметром является модуль зацепления m. Однако на практике диаметр dωЧ окружности нарезки червяка определяется коэффициентом q диаметра червяка, выбираемого в зависимости от нагруженности пары и передаваемой редуктором мощности:
Коэффициент диаметра червяка – экспериментальная величина, определяющаяся по практическим рекомендациям, безразмерна. Тогда:
Зазор у червячной пары берется несколько меньше, чем в зубчатой передаче. Основной габаритной величиной для ступени передачи является межосное расстояние аωЧ,Ч.К., выносимое в марку червячного редуктора и являющееся основной расчетной величиной при расчете пары на прочность:
Расчет червячной передачи на прочность учитывает комплекс сил, действующих в червячной паре. Спираль червяка толкает червячного колеса с осевой силой Qос, вращение червяка приводит к появлению тангенциальной (крутящей) Qt силы, радиальным усилием, действующим от червяка на червячное колесо, является радиальная QR сила (Рис. IX. 20).
Рис. IX. 20 Эти усилия организуют нагрузку червячного колеса: осевое усилие червяка обеспечивает крутящее Ft на червячном колесе, Qt создает осевое усилие Fос для червячного колеса, QR приводит к появлению радиального усилия FR. Все усилия передачи определяются из соотношения, входящего в крутящий момент. В зоне контакта спирали червяка и зуба колеса опасным является контактное напряжение, поэтому основой расчета червячной передачи на прочность является расчет межосного расстояния аωЧ,Ч.К . по эмпирической формуле:
где Е – модуль упругости материала с учетом того, что материалы червяка и червячного колеса одинаковы (в противном случае, в качестве модуля упругости Е берется среднее арифметическое модулей упругости червяка и червячного колеса); Мкр – крутящий момент на червячном колесе; zЧ . – число витков на червяке; zЧ.К. – число зубьев на червячном колесе; Кр – коэффициент режима, зависящий от частоты остановок и включений, а также реверсирования (обратного хода) вращения червяка; Контактное напряжение [ σк ] не рассчитывается, а выводится по полуэмпирической формуле:
где 2 НВ – число единиц твердости поверхности червяка, определенное методом Бринелля. Таким образом, расчет червячной пары основывается на выборе элементарного габаритного параметра q червяка с последующим расчетом межосевого расстояния аωЧ,Ч.К. червяка и червячного колеса.
Рис. IX. 21 Конструкция червячного зацепления обычно компонуется таким образом, что червячное колесо – составное. В связи с большим трением в зоне контакта для червяка выбирается материал более прочный, чем для червячного колеса. Для колеса выбираются материалы с достаточной прочностью, но с меньшим коэффициентом трения. Ради понижения трения могут применяться цветные металлы и сплавы, что очень дорого, поэтому червячное колесо составное, где основной контур – ступица – выполняется из стали с последующей заливкой бронзой (Рис. IX. 21).
Шестеренные насосы. Шестеренные насосы служат для перекачивания жидкостей различной вязкости. В качестве рабочего органа в шестеренных насосах используется шестерня (Рис. IX. 22).
Рис. IX. 22 В корпусе насоса зубья колес находятся в зацеплении, и вращение одного (ведомого) колеса приводит к движению другого (ведомого) колеса. Принцип действия насоса основан на перемещении жидкости, находящейся между зубьями колес. Жидкая фаза, поступая в межзубное пространство, переносится вращением ведомого колеса в зону нагнетания и выжимается ответным зубом. Производительность Q шестеренного насоса определяется площадью f поперечного сечения пространства между зубьями колес, числом z зубьев колес, шириной b зуба и числом n оборотов:
Очевидно, размерность производительности Q:
Эффективность насоса по производительности определяется объемным коэффициентом полезного действия ηV, зависящим от точности изготовления корпуса и в частности от величины зазоров внутри корпуса, производительности Q и давления нагнетания Рн, создаваемого шестерней в зоне нагнетания (Рис. IX. 22).
|
||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 407; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.26.231 (0.011 с.) |

 ,
,
 ,
, ,
,

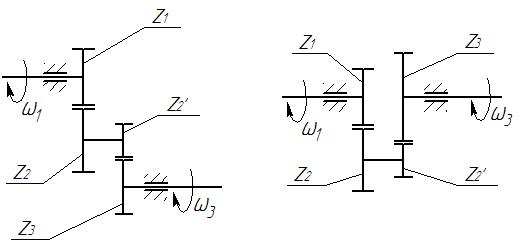
 .
.

 .
. ,
,

 ,
, .
. .
. ,
, .
. .
.
 .
.



 .
. ,
, .
. ,
, .
.

 ,
,
 .
. ,
, .
. .
.
 ,
, ,
,

 .
. .
.


