
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет детали на скручивание.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим модель горизонтальной жестко заделанной балки и мысленно выделим из нее элементарный участок (Рис. V.4).
Рис. V.4
Если γ – угол поворота балки – постоянный, то со временем меняется и угол поворота сечения dφ, тогда длина дуги bb ' равна:
где ρ – расстояние от оси балки до элементарной площадки сечения (Рис. V.5, а).
а) б) Рис. V.5
Тогда:
При использовании формулы (V.1), получим:
Из закона распределения касательных напряжений следует, что крутящий момент dМz в сечении представляет собой равнодействующий момент касательных напряжений в сечении:
где dA – площадь элементарной площадки. Тогда полный внутренний крутящий момент Мz:
или:
Из курса теоретической механики известно:
где Iρ - полярный момент инерции сечения. Тогда используя формулу (V.2), получим формулу распределения касательного напряжения по сечению:
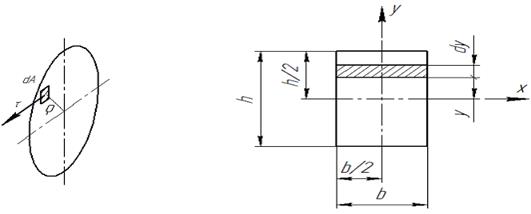
Значение касательного напряжения определяется величиной радиуса ρ от оси балки до элементарной площадки сечения (Рис. V. 6):
Рис. V. 6 если ρ =0, то τ =0 если ρ =max= d /2, то τ =max. Внутренняя зона (ρ ~0) не сопротивляется скручиванию, поэтому валы обычно делают с осевым отверстием, т.е. валы кольцевого сечения.
Оценка деформации вала заключается в определении угла поворота φ вала под действием крутящего момента:
тогда:
Произведение Iρ · G является механической характеристикой материала и называется жесткостью.
Iρ – геометрическая характеристика сечения, которая показывает закономерность распределения элементарных площадок по всему сечению, при этом описывает способность сечения сопротивляться скручиванию. Размерность полярного момента инерции сечения:
Размерность полярного момента выводится из расчета статистического момента сечения, определяемым интегралом:
тогда:
для балки прямоугольного сечения основной геометрической характеристикой при расчете на прочность является осевой момент инерции сечения Ix (Рис. V. 5, б):
Если радиус ρ разложить по теореме Пифагора:
то полярный момент инерции сечения равен:
тогда для круглого сечения:
Часто вместо полярного момента инерции сечения используется полярный момент сопротивления Wρ:
VI. Изгиб.
Изгиб – деформация тела балки под действием сил в продольных плоскостях. Изгиб бывает поперечный (происходит под действием сил и моментов), чистый (действует только изгибающий момент) или плоский (ось балки прогибается в одной плоскости). Рассмотрим случай чистого изгиба (Рис. VI.1) – балка изогнута под действием изгибающих моментов.
Рис. VI. 1
Исходя из характера деформации балки можно установить, что при чистом изгибе происходит поворот поперечных сечений без искажения, тогда как продольные слои балки деформируются (сжимаются и растягиваются) (Рис. VI. 2).
Рис. VI. 2
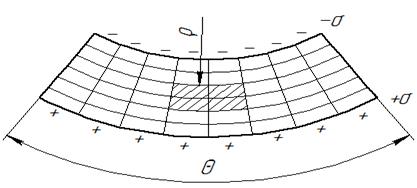
θ – угол поворота торца. Как видно из рис. VI. 2 на выпуклой стороне слои балки растягиваются, что приводит к появлению положительного напряжения (+ σ), а на вогнутой – сжимаются, с возникновением отрицательного напряжения (– σ). В средней зоне, т.е. на оси балки, нет напряжений и нет деформаций – это нейтральный слой (нейтральная ось), длина которого не меняется. С целью вывода формул для определения нормального напряжения и кривизны балки рассмотрим элементарный участок длиной l (Рис. VI. 3).
Рис. VI. 3 Исходная длина балки – ОО1, dθ – угол поворота торцевых перемещений, у – расстояние от нейтральной оси до некоторого слоя. Если из точки О провести линию, параллельную правому торцу, дуга bc будет равна ОО1, а дуга аb – абсолютному удлинению торцов изгиба, т.е.:
тогда относительная деформация равна:
или
тогда:
Введем величину k, называемую собственной кривизной и равную:
Из аналитической геометрии следует:
Степень в знаменателе формулы (VI. 3) существенно не влияет на равенство в связи с тем, что деформации жесткой балки малы, т.е. ими можно пренебречь, тогда:
Применяя закон Гука:
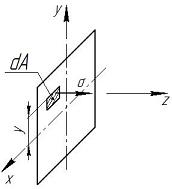
и формулы (VI. 1) и (VI. 2), получим формулу для определения нормального напряжения в любом слое балки (Рис. VI. 4):
Рис. VI. 4 Напряжение σ и его плечо у образует момент, тогда для элементарной площадки можно вывести формулу внутреннего изгибающего момента dMx:
полный внутренний изгибающий момент Mx равен:
или
где
тогда:
следовательно:
Формула (VI. 4) позволяет вести расчет на прочность сечения изогнутой балки. Но на практике обычно вместо осевого момента инерции сечения Ix используют осевой момент сопротивления сечения Wx, равный:
Физический смысл Ix сводится к тому, что эта величина – геометрическая характеристика сечения, описывающая закономерность распределения элементарных площадок по всему сечению, а так же показывающая способность сечения сопротивляться изгибу. Таким образом, условием статической прочности балки при изгибе является выражение:
В зависимости от расстояния между элементарной площадкой сечения и осью балки изменяется напряжение при изгибе (Рис. VI. 5): чем дальше элементарная площадка от оси, тем больше величина напряжения (формула (VI. 4)).
Рис. VI. 5 В связи с этим рациональным является использование именно балки прямоугольного сечения, называемые двутаврами, средний слой которой не сопротивляется изгибу (Рис. V. 6).
Рис. VI. 6
Деформации изогнутой балки. Основной целью анализа изгиба балки является определение максимального прогиба уmax и наибольшего угла поворота θmax изогнутой балки. Пусть на жестко заделанную балку длиной l действует некоторая сила F (Рис. VI.7).
Рис. VI. 7
Для вывода уравнений, позволяющих определить уmax и θmax, воспользуемся уравнением изогнутой балки:
тогда:
или
константа С определяется наложением граничных условий, данных для данной балки, а именно: - если z =0, то у =0 и θ =0; - если z = l, тогда y =max и тогда С =0, а значит:
тогда:
Проинтегрируем уравнение (VI. 6):
константа D =0, тогда:
VII. Сложное нагружение. Гипотезы прочности. Сложное нагружение возникает в тех случаях, когда элемент конструкции подвергается одновременно нескольким простейшим деформациям. В таком случае полностью корректный расчет детали на прочность мы осуществить не можем. Обычно множество напряжений рассчитываемой детали сводят к простейшим схемам (главным площадкам), в которых работают либо только нормальные, либо только касательные напряжения (Рис. VII. 1), причем принято, что:
Рис. VII. 1
Для получения расчетных формул для того или иного вида нагружения выдвигаются некоторые гипотезы (теории) прочности, смысл которых заключается в подборе некоторой эквивалентной величины напряжения, которая сравнивается с допускаемым напряжением. В настоящее время применяют несколько теорий прочности: 1. Эквивалентное напряжение σэкв принимается равным максимальному нормальному напряжению σmax, не превышающему допускаемое напряжение [ σ ]:
2. Разрушение детали происходит по мере достижения максимальных деформаций в материале детали:
где μ – коэффициент пропорциональности. Однако эта теорема не применима в связи с расчетом σ1, σ 2, σ3. 3. На любой наклонной площадке структурного материала детали наиболее опасным напряжением для материала является касательное напряжение:
4. Энергетическая. Разрушение детали происходит по мере накопления и распределения энергии в структуре материала детали:
Разница между третьей и четвертой теориями прочности сводится к тому, что четвертая теория учитывает меньшее касательное напряжение, а значит, и при расчете обеспечивает прочность при минимальной схеме оборудования, но при этом требует проверочного расчета и дополнительного определения физико-механических характеристик материала. Третья теория обеспечивает прочность детали при большей металлоемкости оборудования и не требует дополнительных расчетов, поэтому весьма широко используется в обычном машиностроении. Четвертая гипотеза более строгая, требует более качественного материала, более точных методов проектирования, изготовления и в основном используется в авиационной технике.
Расчет вала. Рассчитаем вал редуктора зубчатой передачи (Рис. VII. 2).
Рис. VII. 2
На зубчатое колесо, закрепленное на валу, с силой F действует ответное колесо, наряду с этим на вал действует вращающий момент М. Таким образом, крутящий Мz (Рис. VII. 3, а) и изгибающий Mx (Рис. VII. 3, б) моменты создают кручение с изгибом.
а) б) Рис. VII. 3 Для расчета габаритных размеров вала применим третью гипотезу прочности:
где касательные τ и нормальные σ напряжения рассчитываются по формулам:
и
где Wρ – полярный момент сопротивления сечения, равный:
Wx – осевой момент сопротивления сечения:
Тогда:
где:
Условие прочности вала:
тогда:
Рассчитываемый диаметр d вала:
|
|||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 851; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.134.162 (0.012 с.) |


 ,
,
 .
. . (V.2)
. (V.2) ,
,
 .
. ,
,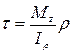 .
.
 ,
, .
. .
. ,
,
 .
. ,
,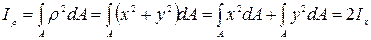 ,
,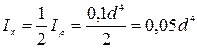 .
. .
.

 ,
,
 ,
, . (VI. 1)
. (VI. 1)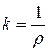 . (VI. 2)
. (VI. 2) . (VI. 3)
. (VI. 3) .
.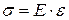
 .
.
 ,
,
 ,
, - осевой момент инерции сечения Ix,
- осевой момент инерции сечения Ix, ,
, . (VI. 4)
. (VI. 4) .
. .
.


 , (VI. 5)
, (VI. 5)
 ,
, =θ=max,
=θ=max, , (VI. 6)
, (VI. 6) .
. ,
, .
. .
.
 .
.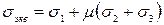 ,
, .
. .
.

 ,
,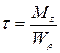
 ,
, ,
, .
. ,
, .
. ,
, .
. .
.


