Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
I. Надежность машин и критерии работоспособности.Содержание книги
Поиск на нашем сайте
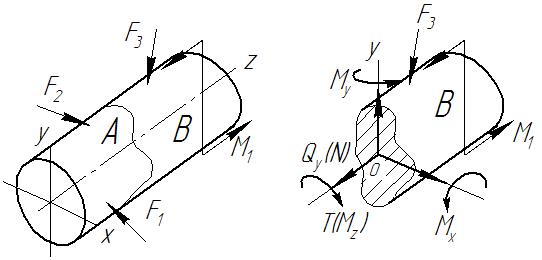
II. Нагрузки Разнообразие тел с различными габаритными параметрами можно свести к трем основным типам. Для определения каждого из таких типов рассмотрим тело (Рис. II. 1).
Рис. II. 1 В зависимости от соотношений величин размеров х1, х2 и х3 тела делятся на: - балка, у которой х1 >> х2, х3 ; - плита (или пластина), у которой х3, х1 >> х2; - массив, где х1 ~ х2 ~ х3 . Все нагружения (нагрузки) – силы, действующие на тело, рассматриваются как внешние и внутренние. Последние, в свою очередь, делятся на активные и реактивные силы, которые обусловлены требованиями условия эксплуатации. Возникновение внутренних силовых факторов связано со стремлением материала сохранять свое первоначальное состояние. Внутренние силовые факторы могут быть статическими, когда влияние силы или момента сил не изменяется в течение времени, и динамическими, когда силовые факторы изменяются во времени. В зависимости от площади поверхности действия, силы делят на концентрированные (приложенные к точке или малой поверхности детали) и распределенные по объему поверхности или длине детали.
а) б) Риc. II. 2 Внешние силы F i задаются из условий эксплуатаций, либо определяются уравнениями равновесия для данной детали. В то же время внутренние усилия Q i определяются с использованием метода сечений, который сводится к тому, что деталь мысленно рассекается на части, и рассматривается выделенная часть в равновесии под действием внешних и внутренних сил (Рис. II. 2, а). Поскольку вся деталь находится в равновесии, то и выделенная часть этой детали находится в равновесии, что обеспечивает взаимодействие внешних и внутренних силовых факторов, при этом внутренние силы рассматриваются в приложении относительно выбранных осей координат. К примеру, горизонтальное равновесие обеспечивается комплексом внешних и внутренних сил (Рис. II.2, б), неопрокидывание обусловливается моментом кручения Т – суммой моментов внутренних сил относительно оси 0z, условием неповорота вокруг осей 0х и 0у является сумма моментов внутренних и внешних сил относительно оси 0х и 0у соответственно. Таким образом, условие равновесия описывается шестью уравнениями:
Физический смысл метода сечений сводится к тому, что равновесие выделенного участка рассматривается под действием внешних и внутренних силовых факторов. Однако на практике редко используют систему из шести уравнений (объясняется неудобством решения данной системы), поэтому обычно рассматривают отдельные случаи: - если N не равно 0, все остальные силовые факторы нулевые, то это случай сжатия или растяжения; - если Qx, Qy не равны 0, то это случай среза; - если Mz и Т не равны 0, то это означает, что деталь подвержена чистому кручению; - если Mуi(внутр.) и Mуi(внешн..) не равны 0, тогда равновесие обеспечивает чистый изгиб. На практике чаще наблюдается случай сложного нагружения.
а) б) Рис. II. 3 Наличие внутренних силовых факторов приводит к тому, что в сечении возникает механическое напряжение Р – удельная сила, мера интенсивности нагружения детали (Рис. II.3, а). Напряжение Р определяется как векторная сумма векторов всех непрерывно распределенных по сечению внутренних сил, т.е. Р – внутреннее усилие сечения. Удельная величина p:
где А – площадь поперечного сечения детали. Для удобства Р раскладывается на проекции на основные оси: σ - нормальное напряжение, τ - касательное напряжение (Рис. II.3, а).
Рассмотрим нагружение на наклонной площадке (Рис. II.3, б). Величина напряжения зависит от ориентации сечения, так как величина площади сечения является функцией угла α:
Так, для балки с площадью А поперечного сечения при действии некоторой силы F напряжение ρ равно:
где N – реактивная сила, тогда:
При разложении вектора ρ на проекции σα и τα, получим:
Используя формулы (II. 1) и (II. 2), определим максимальные значения нормального (σα) и касательного (τα) напряжений. Очевидно, что σα максимально, если косинус угла α равен единице, тогда α равен нулю, т.е.:
Аналогично, при
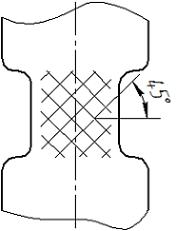
т.е. внутри структуры любого материала имеется множество площадок, каждая из которых имеет свое напряжение. Образец такого материала при разрушении «скашивается» под углом 45º (Рис. II. 4).
Рис. II. 4
Рис. III.1 Для консольной балки в точке заделки реактивной силой является R, которая определяется из уравнения равновесия:
откуда:
Рассмотрим 2 грузовых участка - I и II (Рис. 7, б). Участок I находится в равновесии, т.к. вся балка находится в равновесии, тогда:
откуда:
Продольное усилие N1 положительно, значит направление силы выбрано правильно и – данная сила является растягивающей, т.е. это случай растяжения. Рассуждая аналогичным образом, получим для грузового участка II:
следовательно, усилие N2 на данном участке сжимающее. При построении эпюра продольной силы N необходимо учитывать правило знаков, согласно которому на эпюре проекция N положительна, если вектор силы направлен от сечения, т.е. N растягивающая, если N сжимающая, то ее проекция на эпюре отрицательна. Деформация ∆l балки рассчитывается по закону Гука. Эпюр ∆ l строится с учетом того, что в точке заделки деформация балки равна 0. Данная эпюра позволяет сделать вывод, что наиболее опасное сечение располагается в точке приложения силы F2.
Кручение. Кручение – деформация балки под действием момента, работающего в вертикальной поперечной плоскости (Рис. III.2). Рассмотрим пример кручения жестко заделанной консольной балки (Рис. III.3, а). Разбив балку поперечными сечениями на грузовые участки и отбросив более нагруженные части, с помощью метода сечений построим эпюр крутящих моментов. На участке I (Рис. III.3, б) равновесие будет обеспечиваться при взаимодействии внешнего и внутреннего моментов:
Учитывая правило знаков, согласно которому внутренний крутящий момент положительный, если, глядя на сечение, внутренний крутящий момент поворачивает сечение против часовой стрелки, получим:
или:
Для участка II:
Пусть M1=1 кН·м, M2=3 кН·м, тогда:
Отсюда следует то, что направление Т 2 выбрано неправильно. Изгиб. Изгиб является наиболее сложным видом нагружения. Изгиб – деформация балки под действием моментов в вертикальной продольной или горизонтальной плоскостях (Рис. III.4).
Рис. III. 4 Рассмотрим изгиб консольно заделанной балки (Рис. III.5).
Рис. III.5
Изгибающий момент создается под действием концентрированной силы F. На балку действуют шарнирные опоры А и В, в связи с чем возникают реакции связей – RАy и RВy (Рис. III.6). Расчет балки на прочность сводится к построению эпюров внутренних силовых факторов – поперечной силы Q и изгибающего внутреннего момента Мх. Решение задачи начинается с определения всех реакций связей. Очевидно, что:
Используя метод сечений, мысленно рассечем балку сечениями и, откинув более нагруженную часть грузового участка (l1 или l2), рассмотрим I и II участки.
Рис. III. 7 Рассмотрим участок I (Рис. III.7). Равновесие участка обеспечивается, если воздействию внешней реактивной силы RAy будет противостоять внутренняя сила Q1. Образованная пара сил создает момент, который должен быть скомпенсирован изгибающим моментом Mx1.
Тогда:
Условием неопрокидывания (неповорачивания) является нулевая сумма моментов внешних и внутренних сил относительно точки сечения:
тогда:
Если z =0, то Мх1 =0, если z = l 1, то Мх1 = RAy · l 1. Пусть l 1=1 м, тогда Мх1 = RAy · l 1=1·1=1 кН·м. Внутренний момент Мх1 не является постоянным на участке, в связи с увеличением z, и его проекция на эпюре – наклонная линия.
Аналогичные рассуждения проводятся для участка II (Рис. III.8) и для любых балок с любым видом нагружения.
Рис. III.8
Правила знаков. Внутреннее поперечное усилие Q положительно, если справа от сечения вектор Q направлен вниз, а слева от сечения – вверх, в противном случае Q принимает отрицательное значение (Рис. III.9, а).
а) б) Рис. III.9 Если внутренний изгибающий момент М изгибает балку вниз, то на эпюре его проекция положительна, если вверх – отрицательна (Рис. III.9, б). Замечание. Данное правило определения знака М применимо только при построении эпюра, при составлении уравнений равновесия используется зависимость знака М от направления вращения момента.
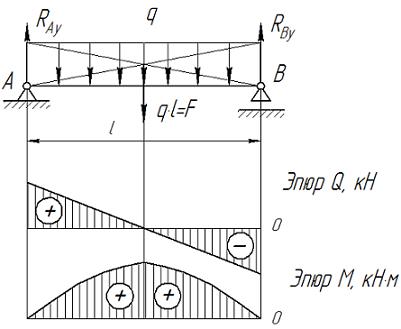
Рассмотрим случай нагружения балки распределенной силой q (Рис. III.10).
Рис. III.10
Очевидно, что:
Рассмотрим участок слева от сечения (Рис. III.11).
Рис. III. 11 Условием вертикального равновесия является уравнение:
откуда:
если z =0, то Q =- RAy, из чего следует то, что направление вектора Q выбрано неправильно. При увеличении z величина Q изменяется, проекция Q является наклонной линией. Условие неопрокидывания:
если z =0, то Мх =0. Из рис. III.10 видно, что балка максимально изогнется в середине балки и, следовательно, опасное сечение – середина балки, тогда как в точках А и В деформации минимальны, тогда: если z = если z =
Правила проверки коррекции построения эпюр. 1. В местах приложения концентрированных внешних силовых факторов на соответствующих эпюрах наблюдаются переходы, равные величине внешних факторов. 2. При наличии концентрированных внешних сил эпюр поперечного усилия Q – горизонталь, а изгибающего момента М – наклонная линия. 3. Если внешняя нагрузка распределена по длине балки, то проекция Q на эпюре – наклонная линия, изгибающего момента М – парабола, причем выпуклость параболы – против направления распределенного усилия. 4. Поскольку
то знак производной от Мх соответствует знаку поперечного усилия Q. V. Сдвиг, кручение. Сдвиг. Пусть на вертикальную жестко заделанную у основания балку действует некоторая сила F (Рис. V.1). При этом слои материала пытаются сдвинуться, чем обусловлено появлением деформаций сдвига. Угол сдвига γ мал, вследствие чего мы можем принять его равным тангенсу γ, который определяется:
или из закона Гука:
G – модуль поперечной упругости (модуль упругости II роду), равный:
коэффициент Пуассона μ для стали – около 0,3, что означает:
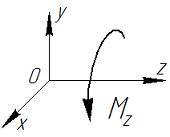
Кручение. Кручение – деформации, появляющиеся при действии на деталь момента, работающего в поперечной вертикальной плоскости и – стремящего повернуть сечение детали (балки) (Рис. V.2).
Рис. V. 2 При действии крутящего момента на жестко заделанную балку сечение балки поворачивается на максимальный угол γ, аналогичный углу поворота при сдвиге (Рис. V.3).
Рис. V. 3 При решении задач на сдвиг и кручение принимаются некоторые допущения (гипотезы): - гипотеза плоских и жестких сечений, согласно которой при повороте сечения оно остается плоским и жестким; - при скручивании деталь-цилиндр поворачивается и остается прямолинейной.
VI. Изгиб.
Изгиб – деформация тела балки под действием сил в продольных плоскостях. Изгиб бывает поперечный (происходит под действием сил и моментов), чистый (действует только изгибающий момент) или плоский (ось балки прогибается в одной плоскости). Рассмотрим случай чистого изгиба (Рис. VI.1) – балка изогнута под действием изгибающих моментов.
Рис. VI. 1
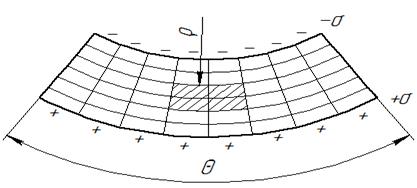
Исходя из характера деформации балки можно установить, что при чистом изгибе происходит поворот поперечных сечений без искажения, тогда как продольные слои балки деформируются (сжимаются и растягиваются) (Рис. VI. 2).
Рис. VI. 2
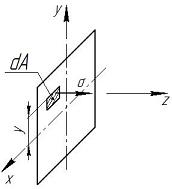
θ – угол поворота торца. Как видно из рис. VI. 2 на выпуклой стороне слои балки растягиваются, что приводит к появлению положительного напряжения (+ σ), а на вогнутой – сжимаются, с возникновением отрицательного напряжения (– σ). В средней зоне, т.е. на оси балки, нет напряжений и нет деформаций – это нейтральный слой (нейтральная ось), длина которого не меняется. С целью вывода формул для определения нормального напряжения и кривизны балки рассмотрим элементарный участок длиной l (Рис. VI. 3).
Рис. VI. 3 Исходная длина балки – ОО1, dθ – угол поворота торцевых перемещений, у – расстояние от нейтральной оси до некоторого слоя. Если из точки О провести линию, параллельную правому торцу, дуга bc будет равна ОО1, а дуга аb – абсолютному удлинению торцов изгиба, т.е.:
тогда относительная деформация равна:
или
тогда:
Введем величину k, называемую собственной кривизной и равную:
Из аналитической геометрии следует:
Степень в знаменателе формулы (VI. 3) существенно не влияет на равенство в связи с тем, что деформации жесткой балки малы, т.е. ими можно пренебречь, тогда:
Применяя закон Гука:
и формулы (VI. 1) и (VI. 2), получим формулу для определения нормального напряжения в любом слое балки (Рис. VI. 4):
Рис. VI. 4 Напряжение σ и его плечо у образует момент, тогда для элементарной площадки можно вывести формулу внутреннего изгибающего момента dMx:
полный внутренний изгибающий момент Mx равен:
или
где тогда:
следовательно:
Формула (VI. 4) позволяет вести расчет на прочность сечения изогнутой балки. Но на практике обычно вместо осевого момента инерции сечения Ix используют осевой момент сопротивления сечения Wx, равный:
Физический смысл Ix сводится к тому, что эта величина – геометрическая характеристика сечения, описывающая закономерность распределения элементарных площадок по всему сечению, а так же показывающая способность сечения сопротивляться изгибу. Таким образом, условием статической прочности балки при изгибе является выражение:
В зависимости от расстояния между элементарной площадкой сечения и осью балки изменяется напряжение при изгибе (Рис. VI. 5): чем дальше элементарная площадка от оси, тем больше величина напряжения (формула (VI. 4)).
Рис. VI. 5 В связи с этим рациональным является использование именно балки прямоугольного сечения, называемые двутаврами, средний слой которой не сопротивляется изгибу (Рис. V. 6).
Рис. VI. 6
Деформации изогнутой балки. Основной целью анализа изгиба балки является определение максимального прогиба уmax и наибольшего угла поворота θmax изогнутой балки. Пусть на жестко заделанную балку длиной l действует некоторая сила F (Рис. VI.7).
Рис. VI. 7
Для вывода уравнений, позволяющих определить уmax и θmax, воспользуемся уравнением изогнутой балки:
тогда:
или
константа С определяется наложением граничных условий, данных для данной балки, а именно: - если z =0, то у =0 и θ =0; - если z = l, тогда y =max и тогда С =0, а значит:
тогда:
Проинтегрируем уравнение (VI. 6):
константа D =0, тогда:
VII. Сложное нагружение. Гипотезы прочности. Сложное нагружение возникает в тех случаях, когда элемент конструкции подвергается одновременно нескольким простейшим деформациям. В таком случае полностью корректный расчет детали на прочность мы осуществить не можем. Обычно множество напряжений рассчитываемой детали сводят к простейшим схемам (главным площадкам), в которых работают либо только нормальные, либо только касательные напряжения (Рис. VII. 1), причем принято, что:
Рис. VII. 1
Для получения расчетных формул для того или иного вида нагружения выдвигаются некоторые гипотезы (теории) прочности, смысл которых заключается в подборе некоторой эквивалентной величины напряжения, которая сравнивается с допускаемым напряжением. В настоящее время применяют несколько теорий прочности: 1. Эквивалентное напряжение σэкв принимается равным максимальному нормальному напряжению σmax, не превышающему допускаемое напряжение [ σ ]:
2. Разрушение детали происходит по мере достижения максимальных деформаций в материале детали:
где μ – коэффициент пропорциональности. Однако эта теорема не применима в связи с расчетом σ1, σ 2, σ3. 3. На любой наклонной площадке структурного материала детали наиболее опасным напряжением для материала является касательное напряжение:
4. Энергетическая. Разрушение детали происходит по мере накопления и распределения энергии в структуре материала детали:
Разница между третьей и четвертой теориями прочности сводится к тому, что четвертая теория учитывает меньшее касательное напряжение, а значит, и при расчете обеспечивает прочность при минимальной схеме оборудования, но при этом требует проверочного расчета и дополнительного определения физико-механических характеристик материала. Третья теория обеспечивает прочность детали при большей металлоемкости оборудования и не требует дополнительных расчетов, поэтому весьма широко используется в обычном машиностроении. Четвертая гипотеза более строгая, требует более качественного материала, более точных методов проектирования, изготовления и в основном используется в авиационной технике.
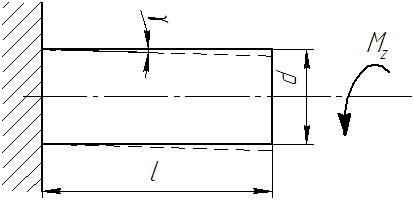
Расчет вала. Рассчитаем вал редуктора зубчатой передачи (Рис. VII. 2).
Рис. VII. 2
На зубчатое колесо, закрепленное на валу, с силой F действует ответное колесо, наряду с этим на вал действует вращающий момент М. Таким образом, крутящий Мz (Рис. VII. 3, а) и изгибающий Mx (Рис. VII. 3, б) моменты создают кручение с изгибом.
а) б) Рис. VII. 3 Для расчета габаритных размеров вала применим третью гипотезу прочности:
где касательные τ и нормальные σ напряжения рассчитываются по формулам:
и
где Wρ – полярный момент сопротивления сечения, равный:
Wx – осевой момент сопротивления сечения:
Тогда:
где:
Условие прочности вала:
тогда:
Рассчитываемый диаметр d вала:
Рис. VIII. 4 При расчетах концентраторы оцениваются с помощью эффективного коэффициента концентратора напряжений k σ, определяемым пределом выносливости σ -1 образца детали без концентраторов напряжения и пределом выносливости σ ΄-1 образца с концентраторами напряжений:
2. Частота обработки поверхности – сочетание выступов и впадин на поверхности детали, которое представляет собой изначальные трещины, которые при циклическом нагружении развиваются, что приводит к более раннему износу детали. Поэтому в реальном проектировании наиболее ответственные места шлифуются. В практике проектирования фактор шероховатости оценивается экспериментально:
где εσ – коэффициент влияния шероховатости; σ ΄-1 – предел выносливости реальной шероховатой детали; σ -1 – предел выносливости полированного образца.
3. Габаритность детали. Практика показывает, что в при больших габаритах детали большая вероятность появления и развития внутренних дефектов. Так, большие заготовки для валов гидротурбин изготавливаются тщательнее, вследствие того, что чаще всего в них встречаются дефекты. Для оценки габаритности детали вводят коэффициент габаритности βσ:
где σ ΄-1 – предел выносливости реального габарита детали; σ -1 – предел выносливости образца. При расчете детали машины на усталостную прочность учитываются все эти коэффициенты, при этом вводится общий коэффициент запаса прочности n, определяемый пределом выносливости σ -1 материала данной детали и эквивалентным напряжением σэкв:
Среднее значение коэффициента запаса прочности n определяется коэффициентами запаса прочности при изгибе nσ и nτ – при кручении:
Эквивалентное напряжение σэкв, в свою очередь, учитывает параметры циклических нагружений – амплитуду нагружения σа и среднее напряжение σm детали:
где ψ – коэффициент, учитывающий влияние цикла на структуру материала детали. Усталость – опасное явление, поэтому все машины рассчитываются на выносливость. При этом расчет ведется в два этапа: оценивается статическая прочность проектируемой детали (на основании чего определяются геометрические характеристики детали), после чего проводится расчет на усталостную прочность уже для готовой конструкции.
Фрикционные передачи. Принцип работы фрикционных передач основан на трении. в связи с чем фрикционные передачи имеют отличительную особенность – необходимость поджатия одного диска передаточного устройства к другому, для чего один из дисков устанавливают на несмещаемой опоре (Рис. IX. 2).
Рис. IX. 2
Сила P, передающаяся от ведущего диска 1 к ведомому диску 2, связана с усилием поджатия F в соотношении:
где f – коэффициент трения дисков; β – коэффициент запаса передаваемого усилия. Передаточное отношение фрикционной передачи зависит от соотношения диаметров ведущего 1 и ведомого 2 колес:
Достоинствами фрикционных передач являются простота устройства, бесшумность работы и плавность движения. Однако они используются в механизмах, передающих небольшие усилия, что связано с эффектом проскальзывания одного диска по другому. Вызванное этим непостоянство передаточного отношения, а также необходимость использования больших усилий поджатия, является основным недостатком фрикционных передач с точки зрения кинематики.
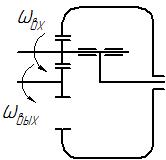
Ременные передачи. Ременные передачи, а также цепные передачи и передачи с использованием тросов, широко используются в производстве. Основной тяговый орган ременной передачи – ремень, помещенный на шкиве (Рис. IX. 3). По виду ремня передачи подразделяются на: - плоскоременные (ремень выполнен из резинотканевой ленты):
- ременно-зубчатые (ремень с зубьями):
Используются в роторно-таблетных аппаратах, а также устройствах, где требуется обеспечить достаточную прочность в передачи вращательного движения. - круглоременные передачи используются в малогабаритных установках:
- клиноременные передачи, наиболее часто используемые в технике:
Передача вращения происходит вследствие фрикционного взаимодействия ремня и поверхности канавки. Вставленные в резину тросики укрепляют ремень, тем самым способствуя передаче больших усилий. - поликлиновые:
Ремни фрикционных передач являются стандартными изделиями. Подбор ремня клиноременной передачи проводится с использованием справочных материалов, в которых даны марки ремней – А,О и т.д. (Рис. IX. 3).
Рис. IX. 3 Основным элементом расчета фрикционных передач на прочность является оценка сечения ремня. Так, для клиноременной передачи рассчитывается количество ремней z:
где N 0 – общая передаваемая мощность; N 1 – стандартная передаваемая мощность; С 1 – поправочный коэффициент, учитывающий удлинение ремня при работе; С 2 – поправочный коэффициент, определяемый различными растяжениями ремней при использовании нескольких ремней в передаче; С 3 – погрешность передачи, связанная с тем, что ремни с большим сечением приводят к большей погрешности. Немаловажным при подборе ремня является и то, что материал ремня в результате работы лохматится и пылится.
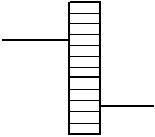
Зубчатые передачи. Данный вид механических передач лишены недостатков по-сравнению с фрикционными передачами. Главное достоинство зубчатых передач – отсутствие проскальзывания, т.е. постоянство передаточного отношения и возможность передачи больших мощностей. Особенность передачи заключается в большой металлоемкости, а значит, механизмы зубчатых передач имеют значительный вес и зачастую повышенную шумность при передачи крутящего момента. По степени подвижности осей вращения зубчатые передачи классифицируются на: - передачи с неподвижными осями (передачи обыкновенного ряда):
- передачи с подвижными осями или хотя бы одной подвижной осью:
Ось зубчатого колеса входного вала подвижна относительно оси выходного вала, т.е. колесо входного вала обкатывается по колесу выходного вала. Колесо, работающее на подвижной оси, называется сателлитом. Передачи, в которых хотя бы одна ось подвижна, называются планетарными редукторами. По взаиморасположению осей вращения зубчатые передачи бывают: - цилиндрические (оси параллельны):
- передачи с пересекающимися осями с коническими шестернями:
- передачи со скрещивающимися осями (червячные передачи):
Ось червяка (ведущего звена) скрещивается с осью червячного колеса (ведомого колеса). По направлению линии зубьев передачи подразделяют на: - прямозубые:
Прямозубые передачи просты по устройству, но более шумны при работе и используются при линейной скорости вращения менее 6 м/с, вследствие повышенной вибрации. - косозубые, где линия направления зубьев не параллельна оси вращения:
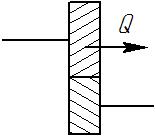
Косозубые передачи дают более плавный ход, что позволяет использовать их при повышенных скоростях, но при этом возникает осевое усилие Q. - шевронные передачи (средняя комбинация направлений зубьев, ослабляющая осевое усилие):
По взаимному расположению колес зубчатые передачи делят на: - передачи с внешним зацеплением:
- передачи с внутренним зацеплением:
По виду профиля зуба передачи могут быть: - с зубьями трапециидального профиля (профиль сечения зуба – трапеция):
- с эвольвентными зубьями:
- с зубьями, очерченными радиусной дугой (зацепление Новикова):
Используетс
|
|||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 373; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.254.112 (0.015 с.) |


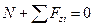 - продольное равновесие;
- продольное равновесие; - поперечное равновесие относительно оси 0у;
- поперечное равновесие относительно оси 0у;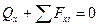 - поперечное равновесие относительно оси 0у;
- поперечное равновесие относительно оси 0у;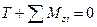 - условие неопрокидывания;
- условие неопрокидывания;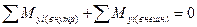 - условие неповорачивания вокруг оси 0у;
- условие неповорачивания вокруг оси 0у;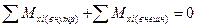 - условие неповорачивания вокруг оси 0х;
- условие неповорачивания вокруг оси 0х;
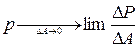 ,
,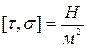 .
.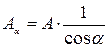 .
.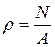 ,
,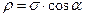 .
.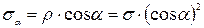 (II. 1)
(II. 1)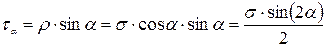 . (II. 2)
. (II. 2)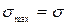 .
.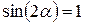 , т.е.
, т.е. 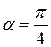
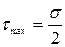 ,
,
 ,
,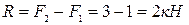 .
. ,
, ,
, .
. ,
, ,
,
 ,
,
 .
. .
. ,
,




 .
.

 ,
,


 .
.


 ,
,

 ,
, ,
, , то Мх =max
, то Мх =max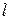 , то Мх =min.
, то Мх =min. ,
, ,
,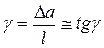
 , (V.1)
, (V.1) где τ – касательное напряжение;
где τ – касательное напряжение;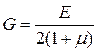 ,
,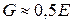 .
.


 ,
,
 ,
, . (VI. 1)
. (VI. 1)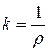 . (VI. 2)
. (VI. 2) . (VI. 3)
. (VI. 3) .
.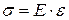
 .
.
 ,
,
 ,
, - осевой момент инерции сечения Ix,
- осевой момент инерции сечения Ix, ,
, . (VI. 4)
. (VI. 4) .
. .
.


 , (VI. 5)
, (VI. 5)
 ,
, =θ=max,
=θ=max, , (VI. 6)
, (VI. 6) .
. ,
, .
. .
.
 .
.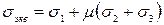 ,
, .
. .
.

 ,
,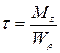
 ,
, ,
, .
. ,
, .
. ,
, .
. .
. .
. ,
, ,
, .
.
 ,
,
 ,
, .
.





 ,
,