
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
III. Расчет деталей на прочность.Содержание книги
Поиск на нашем сайте
Одним из основных этапов расчета детали на прочность является оценка наиболее нагружаемого (опасного) сечения. Анализируется эпюр распределения внутренних силовых факторов – сил, моментов. Для этого используется анализ зависимости внутренних усилий от длины детали. Вид эпюра зависит от вида нагружения.
Растяжение или сжатие. Рассмотрим один из простейших видов нагружения – растяжение (или сжатие) (Рис. III.1, а). Решение задачи начинается с оценки и определения реакций связей с помощью уравнений равновесия. Далее отдельно рассматриваются грузовые участки (участки с одинаковым принципом нагружения), в которых определяются внутренние усилия по длине балки методом сечений.
а) б) Рис. III.1 Для консольной балки в точке заделки реактивной силой является R, которая определяется из уравнения равновесия:
откуда:
Рассмотрим 2 грузовых участка - I и II (Рис. 7, б). Участок I находится в равновесии, т.к. вся балка находится в равновесии, тогда:
откуда:
Продольное усилие N1 положительно, значит направление силы выбрано правильно и – данная сила является растягивающей, т.е. это случай растяжения. Рассуждая аналогичным образом, получим для грузового участка II:
следовательно, усилие N2 на данном участке сжимающее. При построении эпюра продольной силы N необходимо учитывать правило знаков, согласно которому на эпюре проекция N положительна, если вектор силы направлен от сечения, т.е. N растягивающая, если N сжимающая, то ее проекция на эпюре отрицательна. Деформация ∆l балки рассчитывается по закону Гука. Эпюр ∆ l строится с учетом того, что в точке заделки деформация балки равна 0. Данная эпюра позволяет сделать вывод, что наиболее опасное сечение располагается в точке приложения силы F2.
Кручение. Кручение – деформация балки под действием момента, работающего в вертикальной поперечной плоскости (Рис. III.2). Рассмотрим пример кручения жестко заделанной консольной балки (Рис. III.3, а). Разбив балку поперечными сечениями на грузовые участки и отбросив более нагруженные части, с помощью метода сечений построим эпюр крутящих моментов. На участке I (Рис. III.3, б) равновесие будет обеспечиваться при взаимодействии внешнего и внутреннего моментов:
Учитывая правило знаков, согласно которому внутренний крутящий момент положительный, если, глядя на сечение, внутренний крутящий момент поворачивает сечение против часовой стрелки, получим:
или:
Для участка II:
Пусть M1=1 кН·м, M2=3 кН·м, тогда:
Отсюда следует то, что направление Т 2 выбрано неправильно. Изгиб. Изгиб является наиболее сложным видом нагружения. Изгиб – деформация балки под действием моментов в вертикальной продольной или горизонтальной плоскостях (Рис. III.4).
Рис. III. 4 Рассмотрим изгиб консольно заделанной балки (Рис. III.5).
Рис. III.5
Изгибающий момент создается под действием концентрированной силы F. На балку действуют шарнирные опоры А и В, в связи с чем возникают реакции связей – RАy и RВy (Рис. III.6). Расчет балки на прочность сводится к построению эпюров внутренних силовых факторов – поперечной силы Q и изгибающего внутреннего момента Мх. Решение задачи начинается с определения всех реакций связей. Очевидно, что:
Используя метод сечений, мысленно рассечем балку сечениями и, откинув более нагруженную часть грузового участка (l1 или l2), рассмотрим I и II участки.
Рис. III. 7 Рассмотрим участок I (Рис. III.7). Равновесие участка обеспечивается, если воздействию внешней реактивной силы RAy будет противостоять внутренняя сила Q1. Образованная пара сил создает момент, который должен быть скомпенсирован изгибающим моментом Mx1.
Тогда:
Условием неопрокидывания (неповорачивания) является нулевая сумма моментов внешних и внутренних сил относительно точки сечения:
тогда:
Если z =0, то Мх1 =0, если z = l 1, то Мх1 = RAy · l 1. Пусть l 1=1 м, тогда Мх1 = RAy · l 1=1·1=1 кН·м. Внутренний момент Мх1 не является постоянным на участке, в связи с увеличением z, и его проекция на эпюре – наклонная линия. Аналогичные рассуждения проводятся для участка II (Рис. III.8) и для любых балок с любым видом нагружения.
Рис. III.8
Правила знаков. Внутреннее поперечное усилие Q положительно, если справа от сечения вектор Q направлен вниз, а слева от сечения – вверх, в противном случае Q принимает отрицательное значение (Рис. III.9, а).
а) б) Рис. III.9 Если внутренний изгибающий момент М изгибает балку вниз, то на эпюре его проекция положительна, если вверх – отрицательна (Рис. III.9, б). Замечание. Данное правило определения знака М применимо только при построении эпюра, при составлении уравнений равновесия используется зависимость знака М от направления вращения момента.
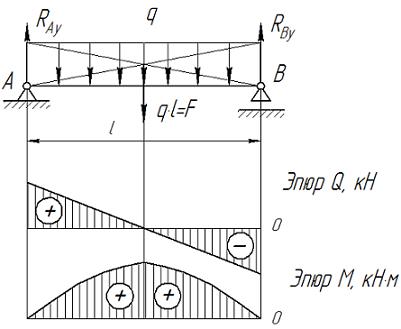
Рассмотрим случай нагружения балки распределенной силой q (Рис. III.10).
Рис. III.10
Очевидно, что:
Рассмотрим участок слева от сечения (Рис. III.11).
Рис. III. 11 Условием вертикального равновесия является уравнение:
откуда:
если z =0, то Q =- RAy, из чего следует то, что направление вектора Q выбрано неправильно. При увеличении z величина Q изменяется, проекция Q является наклонной линией. Условие неопрокидывания:
если z =0, то Мх =0. Из рис. III.10 видно, что балка максимально изогнется в середине балки и, следовательно, опасное сечение – середина балки, тогда как в точках А и В деформации минимальны, тогда: если z = если z =
Правила проверки коррекции построения эпюр. 1. В местах приложения концентрированных внешних силовых факторов на соответствующих эпюрах наблюдаются переходы, равные величине внешних факторов. 2. При наличии концентрированных внешних сил эпюр поперечного усилия Q – горизонталь, а изгибающего момента М – наклонная линия. 3. Если внешняя нагрузка распределена по длине балки, то проекция Q на эпюре – наклонная линия, изгибающего момента М – парабола, причем выпуклость параболы – против направления распределенного усилия. 4. Поскольку
то знак производной от Мх соответствует знаку поперечного усилия Q.
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 311; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.171.72 (0.006 с.) |


 ,
,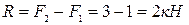 .
. ,
, ,
, .
. ,
, ,
,
 ,
,
 .
. .
. ,
,




 .
.

 ,
,


 .
.


 ,
,

 ,
, ,
, , то Мх =max
, то Мх =max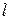 , то Мх =min.
, то Мх =min. ,
, ,
,


