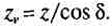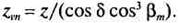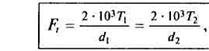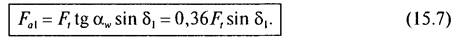Основные геометрические соотношения

В конических зубчатых колесах высота зуба, а следовательно, и мо­дуль зацепления увеличиваются от внутреннего 1 к внешнему 3 до­полнительному конусу (см. рис. 15.3, 15.4). Для удобства измерения

размеры конических колес принято определять по внешнему торцу зуба, образованному внешним дополнительным конусом.

Максимальный модуль зубьев — внешний окружной модуль — полу­чается на внешнем торце колеса. Его обозначают: т_е — для прямозубых колес и т_1е — для колес с круговыми зубьями.

Внешний окружной модуль т_е или т,_е можно не округлять до стан­дартного (см. табл. 11.1), так как одним и тем же режущим инструмен­том можно нарезать колеса с различными значениями модуля, лежа­щими в некотором непрерывном интервале.

Для повышения износостойкости и сопротивления зубьев заеданию конические зубчатые колеса выполняют с высотной модификацией (см. § 11.11), выравнивающей удельные скольжения зубьев шестерни и ко­леса. Значения коэффициентов смещения режущего инструмента х_Л для пря­мозубой шестерни и х„, для шестерни с круговым зубом принимают по табл. 15.1 и 15.2. Коэффициенты смещения для колес соответственно равны:

х_е2 = -х_е1 и х_п2= -х_п1.

Для передач, у которых z и и отличаются от приведенных в табл. 15.1 и 15.2, значения коэффициентов смещения х х_п1 и х_п2, принимают с ок­руглением в большую сторону.

Основные геометрические соотношения для конических зубчатых передач с прямыми и круговыми зубьями даны в табл. 15.3.

Таблица 15.1. Коэффициенты смещения х_Л для конической шестерни с прямыми зубьями

 

м	хп1, при и
1,0	1,25	1,6	2,0	2,5	3,15	4,0
	_	_	_	_	0,50	0,53	0,56
	—	—	0,34	0,42	0,47	0,50	0,52
	—	0,17	0,30	0,38	0,43	0,46	0,48
	0,00	0,15	0,28	0,36	0,40	0,43	0,45
	0,00	0,14	0,26	0,34	0,37	0,40	0,42
	0,00	0,13	0,23	0,29	0,33	0,36	0,38
	0,00	0,11	0,19	0,25	0,28	0,31	0,33

Таблица 15.2. Коэффициенты смещения х,, для конической шестерни с круговыми зубьями

 

г,	хп1, при и
1,0	1,25	1,6	2,0	2,5	3,15	4,0
	_	_	—	0,32	0,37	0,39	0,41
	—	—	0,23	0,29	0,33	0,35	0,37
	—	0,11	0,21	0,26	0,30	0,32	0,34
	0,00	0,10	0,19	0,24	0,27	0,30	0,32
	0,00	0,09	0,17	0,22	0,26	0,28	0,29
	0,00	0,08	0,15	0,19	0,21	0,24	0,25
	0,00	0,07	0,11	0,16	0,18	0,21	0,22

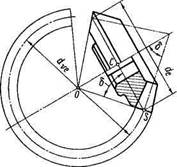
Эквивалентное колесо

Для прямозубой передачи профили зубьев конического колеса, по­строенные на развертке среднего дополнительного конуса (см. рис. 15.3), весьма близки к профилям зубьев эквивалентного цилиндрического прямозубого колеса. Дополнив развертку до полной окружности

(рис. 15.5), получим эквивалентное ци­линдрическое колесо с числом зубь­ев г,..

Из треугольника OCS (рис. 15.5) делительный диаметр эквивалентного колеса

откуда эквивалентное число зубьев:

(15.3)

Для передачи с круговыми зубьями

Рис. 15.5. Схема к определению эквивалентного числа зубьев

профили зубьев конического колеса в нормальном сечении близки к про­филям зубьев эквивалентного цилинд­рического прямозубого колеса с числом зубьев z_v„, полученным двой­ным приведением: конического колеса к цилиндрическому и кругово­го зуба к прямому зубу [см. формулы (15.3) и (14.5)]:

(15.4)

В формулах (15.3) и (15.4) z — действительное число зубьев кони­ческого колеса.

Силы в зацеплении

Силы в конической передаче определяют по размерам сечения на се­редине ширины зубчатого венца, в котором лежит точка приложения силы F_n, действующей перпендикулярно поверхности зуба (рис. 15.6). Силу F_n раскладывают на составляющие: F_n F_r и F_a.

В прямозубой передаче:

радиальная сила на шестерне (при а_w = 20°):

(15.5)

окружная сила на шестерне или колесе:

(15.6)

где Т_х и Т₂ — в Нм; d₁ d₂ — B мм.

 

Рис. 15.6. Схема сил в конической прямозубой передаче (колеса условно раздвинуты)

Осевая сила на шестерне:

Силы на колесе соответственно равны: F_r2 = F_a1; F_a2 = F_rl.

В передаче с круговым зубом во избежание заклинивания зубьев в про­цессе зацепления при значительных зазорах в подшипниках необходимо осевую силу F_a1 на ведущей шестерне направить к основанию делитель­ного конуса. Для этого направление вращения ведущей шестерни (если смотреть со стороны вершины делительного конуса) и направление наклона зубьев должны совпадать (на рис. 11.2, б шестерня 1 вращается по ходу часовой стрелки, т. е. вправо, и зуб шестерни — правый).

В передаче с круговым зубом при соблюдении этого условия ок­ружную силу F, определяют по формуле (15.6);

радиальная сила на шестерне (при а„ = 20°; р„, = 35°)

осевая сила на шестерне (при а_w = 20°; β_m=35°)

Силы на колесе соответственно равны: F_r2 = F_al; F_a2 = F_rl

(15.8)

(15.9)