
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Измерение переменных в социально-экономических и политических исследованияхСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
И ТЕОРИЯ ИНТЕРВАЛЬНОЙ ПОЛЕЗНОСТИ Основные понятия современной теории измерения
Математическое описание социально-экономической реальности означает, что изучаемым явлениям и их взаимоотношениям ставятся в соответствие некоторые вполне определенные формальные объекты со своими отношениями, прежде всего числа и отношения между ними. Измерение — это приписывание объекту по какому-то признаку чисел определенным образом; поэтому математическое моделирование эмпирического материала начинается с измерения. В литературе по математическому моделированию социально-экономических явлений (как зарубежной, так и отечественной) проблеме измерения уделяется чрезвычайно много внимания. Поскольку для наших целей придется пользоваться рядом понятий современной теории измерения, кратко поясним значения основных терминов. Тем более это необходимо сделать в силу того факта, что с современной научной трактовкой проблем теории измерения хорошо знакомы многие специалисты, работающие в области прикладной психологии или конкретной социологии, но как это ни странно, в меньшей степени — многие экономисты, занимающиеся конкретной экономикой или математическими моделями экономики. И хотя нетривиальность измерения индекса цен или показателя сложности конкретного труда известна всем экономистам, сами методы теории измерения, позволяющие измерять, например, уровень социальной мобильности или уровень жизни, известны далеко не всем. Основные вопросы, которые здесь возникают, следующие. Каким способом можно приписать данному объекту число? Когда это можно сделать, когда нельзя? Что можно потом «делать», с этим числом? Зачем вообще приписывать числа реальным объектам? В какой степени по получаемым числам можно судить о свойствах реальности? Известны три основные проблемы теории измерения: представления, единственности, адекватности. Первая заключается в построении шкалы, задающей соответствие между эмпирическим признаком, присущим наблюдаемым объектам, и множеством чисел, «измеряющих» этот признак у разных объектов. Содержательно под шкалой, измеряющей значения признака, можно понимать подмножество действительных чисел, каждое из которых однозначно соответствует некоторому значению признака (т. е. значению, «снимаемому» на данном объекте) и с которым разрешается производить некоторые (не любые) арифметические операции.
Для того чтобы задать определение шкалы более строго, вводится понятие «система с отношениями». Под эмпирической системой с отношениями понимается упорядоченный набор {A; R Иногда наряду с эмпирическим отношением рассматривают эмпирические операции, т. е. переход от одного набора элементов из множества А к другому набору (может быть, состоящему из одного элемента). Самым простым примером операции может служить, например, операция «суммирования двух объемов тела», в результате чего переходят от двух жидких тел с объемами V
Эмпирическое отношение — это то, что важно для исследователя, и то, что он может эмпирически проверить. Если какое-то утверждение о свойстве изучаемых объектов не может быть эмпирически проверено, то данное свойство не может считаться эмпирическим отношением и не может непосредственно входить в какую-либо эмпирическую систему с отношениями. Надо также отметить, что обычно множество А включает в себя всю мыслимую совокупность потенциально возможных элементов, между наборами которых выполняется интересующее нас отношение. Даже если мы рассматриваем лишь некоторый небольшой коллектив, каждого члена которого мы хотим описать с точки зрения, например, признака «трудолюбие», конструируя шкалу с помощью эмпирической системы с отношениями, необходимо включить в множество А всех мыслимых потенциально возможными индивидов с самыми различными уровнями трудолюбия. Кроме того, обычно с каждым признаком, присущим объектам, связывается одно-два, реже три-четыре отношения, а сами отношения, как правило, бывают двухместные, четырехместные (большая размерность отношений встречается реже). Объект, имеющий несколько признаков, которые необходимо «измерить», представляется с помощью нескольких эмпирических систем с отношениями (с одним и тем же множеством А), каждая из которых позволяет измерить только один признак. Итак, пусть установлена эмпирическая система с отношениями w = { A; R Â = { E, Q Пусть размерности Q
Так как для данной эмпирической системы с отношениями, вообще говоря, может быть построено много шкал (различающихся и подмножествами множества действительных чисел, и числовыми отношениями), то необходимо как-то описать все эти шкалы, поскольку они эквивалентны между собой, являясь числовыми моделями одного и того же признака. Проблема единственности имеет своей задачей описание всего множества эквивалентных шкал. Очевидно, если две разные шкалы S1 = { Vi, m1, f1 }, S2 = { Vi, m2, f2 } одной и той же эмпирической системы с отношениями одинаково «различают» или «не различают» объекты Наиболее распространенные примеры таких шкал: абсолютная шкала — j(х)=х. Этой шкалой измеряется, например, число зрителей в кинотеатре; шкала отношений —j (х)=kх, k>0. Эта шкала наиболее распространена, с ее помощью измеряются длина, масса, объем и т. п. Так как от одной шкалы мы переходим к другой, умножая числовое значение на положительное число k, то тем самым шкалы отличаются друг от друга только масштабами; шкала интервалов имеет допустимое преобразование вида j(х)=kx+l, k>0. Этот тип шкалы отличается от предыдущего тем, что переход от измерения в одной шкале к измерениям в другой осуществляется не только умножением на положительное число, но и прибавлением к результату некоторой постоянной. Как известно, переход от значения температуры, выраженной в градусах Цельсия, к значению температуры по Фаренгейту или Реамюру осуществляется именно таким образом, например: t порядковая шкала — такие шкалы отличаются одна от другой монотонным (обычно положительным) преобразованием количественных значений —
номинальная шкала (или шкала наименований) — допускает любое взаимно однозначное преобразование. Обратимся теперь к проблеме адекватности измерений (иногда говорят «осмысленности») — самой важной, по нашему мнению, в теории измерений. Суть ее заключается в определении допустимых процедур пользования получаемыми в измерении числами. Можно ли складывать «полезности» или суммировать и сравнивать между собой «туфли» и «вафли»? Какой содержательный смысл того или иного количественного утверждения? На подобные вопросы дает ответ анализ проблемы адекватности. Всякая эмпирическая наука, применяющая математические методы, имеет дело не только с качественными суждениями, но и с количественными. Числа, с которыми она имеет дело, получаются в результате измерений, в результате использования шкал того или иного типа. Если мы говорим, что «расстояние от Москвы до Нью-Йорка в несколько раз больше расстояния от Москвы до Парижа» или что «реализация программы муниципального жилищного строительства позволит значительно повысить уровень народного благосостояния», то это значит, что имеется реальная возможность определить количественное значение «расстояний» или «уровня благосостояния» и, более того, эмпирически проверить, соответствует ли предикат предмету в данных утверждениях. При этом, поскольку любая из эквивалентных шкал (данного типа) моделирует реальность «одинаково правильно», при эмпирической проверке можно пользоваться любой из них. Количественные утверждения, допускающие операциональную проверку, могут быть самой различной формы, но их истинность или ложность может зависеть от конкретной шкалы, с помощью которой были получены числовые характеристики. Например, если сказать, что «вчера температура воздуха в 12 часов дня была вдвое выше, чем в 15 часов», то утверждение будет соответствовать истине, только если пользоваться какой-то одной определенной шкалой температур, предположим шкалой Цельсия. Если же аналогичное по форме утверждение делается об отношении расстояний или масс, то его истинность или ложность будет одной и той же независимо от масштаба измерения расстояния или масс. Основную ценность в науке имеют такие количественные утверждения, истинность или ложность которых инвариантна относительно допустимых преобразований используемых шкал, т. е. не зависит от конкретного вида используемой шкалы. Именно такие утверждения называются адекватными. Если это не так, то соответствующие количественные утверждения неадекватны и, для того чтобы понять их содержательно, необходимо точно знать, какой конкретно шкалой пользовались. Известно, например, что утверждение о том, какая из двух средних «удовлетворенностей» или «привлекательностей» больше, неадекватно, когда до обычного усреднения в коллективах сами индивидуальные «удовлетворенности» или «привлекательности» измерялись в порядковых шкалах. При одной шкале первый коллектив будет характеризоваться большими величинами, при другой все может быть наоборот.
Если тип шкалы установлен, то можно ставить вопрос относительно адекватности тех или иных количественных утверждений. В таких утверждениях обычно используются какие-то арифметические преобразования шкальных значений и последующие сравнения их между собой и с другими величинами. Поэтому формализовать проблему адекватности — значит выразить с помощью определенных преобразований шкальных значений некоторые математические соотношения и проверить их инвариантность относительно группы допустимых преобразований использованных шкал. В 1972 г. Ю. А. Шеголевым была четко поставлена и решена проблема допустимости числовых операций над шкальными значениями одной и той же переменной. А именно: если значение хп+1получается как вполне определенный результат преобразования значений х1, х2,…, хп: хп+1 =F (х1, х2,…, хп), (3.1) то какой вид должна иметь функция F(х1,..., хп), чтобы равенство (2.1) выполнялось независимо от конкретной шкалы данного типа? Если
Аналогично этой проблеме можно сформулировать задачу на определение общего вида всех таких функций от п независимых переменных, измеренных в одной и той же шкале, значения которых инвариантны относительно допустимых преобразований данной шкалы: Н (х1, х2,…, хп)=H( Предположим, нас интересует вид функций F(х1, x2,…,хп) и Н (х1, x2,…,хп), когда шкала является шкалой отношений (j(х) = кх) или шкалой интервалов (j(х) = кх +l). Как нетрудно видеть, отношение шкальных значений для шкалы отношений х1/x2, не зависит от конкретного вида шкал, а для интервальной шкалы инвариантным оказывается отношение разностей («интервалов») (х1_- x2) / (х На основании этого можно утверждать, что функции F и Н могут иметь вид: F (х1, х2,…, хп)= +хп + (х2—х1) ∙Φ( Н (х1, х2,…, хп) = Φ( где Ф — произвольная функция соответствующего числа аргументов. Однако можно доказать справедливость и обратного утверждения о том, что если некоторые функции F и Н удовлетворяют условиям (3.2) и (3.3) соответственно при любых хj и значениях параметров к, I, то они будут иметь вид типа (2.4) с точностью до перестановок переменных хj. Покажем ход рассуждений для интервальной шкалы типа (2.3). Пусть дифференцируемая функция Н (х1, х2,…, хп) удовлетворяет при любых хj,к, I равенству Н (х1,х2,...,хп ) Требуется вывести необходимые условия на ее вид. Дифференцируя тождество (2.3)' по хj, к, I слева и справа, получим после соответствующих преобразований уравнение - в частных производных, которому должна удовлетворять всякая функция Н (х1, х2,…, хп):
Решением этого уравнения и будет функция типа функции Н из (3.4). Теперь можно ответить на вопрос относительно того, что можно делать с получаемыми в результате измерения числами. Очевидно, что сам по себе вопрос допустимости суммирования или какого-либо другого преобразования шкальных величин не имеет смысла. Необходимо точно указать, какого типа количественное утверждение, проверяемое на адекватность, стоит за этим суммированием. Пусть, например, необходимо выяснить, может ли рассматриваться в качестве некоторой закономерности, инварианта количественное утверждение следующего вида: «Сумма двух величин х+у, измеряемых в интервальной шкале, всегда будет строго больше третьей величины z, измеряемой в той же самой интервальной шкале», т. е. х + у >z. Совершенно очевидно, что это неравенство неадекватно, поскольку переход к величинам х' = кх+l, у' = ку + 1, z'=кz + 1, к>0 дает х' + у'—1>z', что не обязательно означает неравенство х' + у'>z', если константа l х + у>z + в котором величина
то они будут адекватны, если только п = т. В самом деле, соотношение (2.6) равносильно тогда соотношению
если xm < ym; В связи с последним примером отметим один аспект применения теории измерения, имеющий немалое методологическое значение и довольно интенсивно обсуждавшийся прежде. Вопрос ставится так: обязательно ли всем формальным операциям, допустимым с точки зрения адекватности, соответствуют некие реальные эмпирические процедуры? Или некоторым допустимым операциям над шкальными значениями не соответствуют никакие реальные операции? Так, для случая шкалы отношений ( Ln(x1)+ ln(x2 ) – ln(x3) ≥ln(x4)(3.7) Это соотношение адекватно, если все переменные измерены в одной и той же шкале. Имеем ln
Переход к эквивалентной шкале x' = kx дает после несложных преобразований
Откуда ln
т. е. неравенство для сумм и разностей логарифмов адекватно. Но какие эмпирические операции могут стоять за взятием логарифмов, если в эмпирической системе, образующей шкалу отношений, даны лишь сравнения самих объектов и их пар (типа отношений масс или расстояний), но нет никаких логарифмов и т.п.? Аналогично этой ситуации адекватное (при m = n) неравенство (3.6) относится к случаю, когда сравниваются суммы одного и того же числа интервальных шкальных значений; в то же время в соответствующей эмпирической системе явно не присутствуют операции сложения объектов с последующим сравнением: допускается сравнивать лишь сами объекты и пары (порождающие разности шкальных значений). Однако это несоответствие допустимых формальных операций и эмпирической, реальности только кажущееся. Все дело в том, что соотношение (3.7)' формально тождественно соотношению (3.7), а соотношение (3.6)' — соотношению (3.6). Поэтому в формальных выражениях, преобразованиях, сравнениях, если они адекватны, не содержится ничего такого, что не было бы отражением реальности. Отметим еще один момент, связанный с построением шкал и приложениями теории измерения. Очень часто эмпирическая система с отношениями не является, вообще говоря, совокупностью объектов реального мира со своими отношениями, не зависящей от исследователя. Так, например, пытаясь построить переменную, характеризующую некоторое субъективное отношение индивидов к каким-то явлениям внешнего мира, исследователь-социолог формирует специальный набор вопросов, ответы на которые далее позволят построить соответствующую шкалу. В этом случае социологическая анкета является инструментом познания реальности, «прибором», показания которого и будут характеризовать эмпирическую систему с отношениями. Другой, часто встречающийся случай — когда вводится шкала, измеряющая индивидуальную «полезность» некоторого явления, например набора продуктов, потребляемых индивидом в течение фиксированного промежутка времени. Предполагается, что между всевозможными наборами потребления и положительным гиперортантом векторного пространства Е И в том, и в другом случае неудовлетворительный результат измерения не обязательно означает, что в социальной реальности отсутствует возможность измерения некоторых ее свойств; просто «прибор», по которому мы судим о реальности, должен быть усовершенствован, что может быть сделано лишь при осуществлении грамотного анализа результатов измерения. Однако самым главным здесь остается формулировка содержательных гипотез о свойствах реальности, которые должны проверяться эмпирически с помощью получения первичной информации и последующего измерения соответствующих переменных.
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 481; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.132.118 (0.016 с.) |

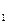 , R
, R 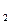 ,..., R
,..., R  }, где А — множество эмпирических объектов, a R
}, где А — множество эмпирических объектов, a R  = V
= V 
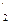
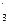
 , совпадают с соответствующими размерностями R
, совпадают с соответствующими размерностями R 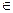 A так удастся подобрать определенное число x
A так удастся подобрать определенное число x  (т. е. f1(а) = f1(b)
(т. е. f1(а) = f1(b)  f2(а) = f2(b), a,b
f2(а) = f2(b), a,b  ) то, значит, между значениями f1(а) и f2(а) существует взаимно однозначное соответствие: f2(а) =
) то, значит, между значениями f1(а) и f2(а) существует взаимно однозначное соответствие: f2(а) =  . Функцию одного переменного у =
. Функцию одного переменного у =  называют тогда допустимым преобразованием шкалы S1. Если все эквивалентные шкалы могут быть получены из одной шкалы с помощью некоторого класса допустимых преобразований {
называют тогда допустимым преобразованием шкалы S1. Если все эквивалентные шкалы могут быть получены из одной шкалы с помощью некоторого класса допустимых преобразований {  }, то тогда можно сказать, что класс {
}, то тогда можно сказать, что класс { 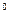 C=(5/9) t
C=(5/9) t  . (3.2)
. (3.2) ).- Отсюда, собственно, и название этих шкал. Верно и обратное: всякое допустимое преобразование
).- Отсюда, собственно, и название этих шкал. Верно и обратное: всякое допустимое преобразование  0 или (х1_- x2)/ (х
0 или (х1_- x2)/ (х 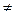 x
x  ),
), ), (3.4)
), (3.4) Н (кх1 + I, кх2 + I,..., кхп + I).(3.3)'
Н (кх1 + I, кх2 + I,..., кхп + I).(3.3)' (3.5)
(3.5) ,
, , (3.6)
, (3.6) , (3.6)’
, (3.6)’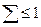 , если хт>ут здесь хотя бы одна разность x
, если хт>ут здесь хотя бы одна разность x  ln(x4), что равносильно неравенству
ln(x4), что равносильно неравенству (x4) (3.7)'
(x4) (3.7)' (x′4)
(x′4)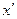 1 + ln
1 + ln 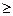 ln
ln  ,п существует изоморфизм и далее под наборами потребления понимаются n-мерные векторы x≥0. Ясно, что и здесь существует промежуточный «прибор» - модель множества наборов потребления в виде гиперортанта.
,п существует изоморфизм и далее под наборами потребления понимаются n-мерные векторы x≥0. Ясно, что и здесь существует промежуточный «прибор» - модель множества наборов потребления в виде гиперортанта.


