Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача рациональности поведения сложнойСодержание книги
Поиск на нашем сайте
Системы
 X, может быть названо рациональным, а когда его нельзя так назвать? Естественно, для того чтобы судить о рациональности или нерациональности поведения некоторой системы, необходимо дать строгое определение рациональности, которое соответствовало бы нашим интуитивным представлениям о разумном поведении. Необходимо определить рациональность так, чтобы исключить возможности всякого рода противоречивости, непоследовательности, неоптимальности и т. п.. Формально можно потребовать, чтобы поведение «рациональной» системы удовлетворяло некоторым «аксиомам рациональности», исключающим противоречивость и непоследовательность выбора. Например, аксиомы выявленного предпочтения определенным образом формализуют представление о рациональности, есть и другие возможности подобной формализации. X, может быть названо рациональным, а когда его нельзя так назвать? Естественно, для того чтобы судить о рациональности или нерациональности поведения некоторой системы, необходимо дать строгое определение рациональности, которое соответствовало бы нашим интуитивным представлениям о разумном поведении. Необходимо определить рациональность так, чтобы исключить возможности всякого рода противоречивости, непоследовательности, неоптимальности и т. п.. Формально можно потребовать, чтобы поведение «рациональной» системы удовлетворяло некоторым «аксиомам рациональности», исключающим противоречивость и непоследовательность выбора. Например, аксиомы выявленного предпочтения определенным образом формализуют представление о рациональности, есть и другие возможности подобной формализации.
Пусть система, состоящая из двух подсистем с целевыми функциями и1(х) и и2(х), выбирает свои состояния из каждого множества А
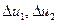 ) (рис. 4.3), причем существенными для нее являются именно «ущербы» ) (рис. 4.3), причем существенными для нее являются именно «ущербы» 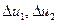 независимо от того, каково множество А, а выбор делается именно из множества независимо от того, каково множество А, а выбор делается именно из множества  или или 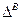 : :
Тогда необходимо признать, что система обладает единым критерием оптимальности z, т. е. является рациональной. Приведенный пример показывает, что понятие рациональности сложной системы неоднозначно. Содержание этого термина зависит от того, какую возможность выбора мы приписываем системе. Однако произвола здесь нет, все определяется алгоритмами взаимодействия подсистем и формирования окончательного состояния. Говоря о предпочтениях и рациональности реальной сложной системы, состоящей из целевых подсистем, можно иметь в виду рациональность реального поведения системы, а можно ограничиться рассмотрением формально принятой рациональности, предпочтения, которое теоретически должно быть у данной системы в соответствии с провозглашаемыми принципами интеграции частных предпочтений в агрегированное. И тот, и другой аспект заслуживают внимание исследователя, так же как и их соотношение. Поэтому для исследователя реальных систем представляют интерес не только предпочтения и принципы их агрегации, но и причины, мешающие их действенности. В частности, наблюдаемое поведение сложной системы может быть не оптимальным по отношению к объявленным целям вследствие недостаточности и недостоверности информации о реальных возможностях; вследствие «ошибок счета», т. е. неправильной обработки информации, неправильной ориентации решений (предпочтений) в некоторых подсистемах, не отражающей необходимых предпочтений или отражающей «паразитные» цели; вследствие искажения самих принципов согласования, приводящего, например, к принятию противоречивых решений, и т.д.
|
||||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 241; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.183.34 (0.008 с.) |

 Как было отмечено, обычно сложная система, состоящая из целевых подсистем, имеет некоторое глобальное предпочтение (целевую функцию u(x)), и с этой точки зрения ее поведение рационально, разумно, поскольку всякий раз делается наилучший выбор в соответствии с этим предпочтением.
Как было отмечено, обычно сложная система, состоящая из целевых подсистем, имеет некоторое глобальное предпочтение (целевую функцию u(x)), и с этой точки зрения ее поведение рационально, разумно, поскольку всякий раз делается наилучший выбор в соответствии с этим предпочтением.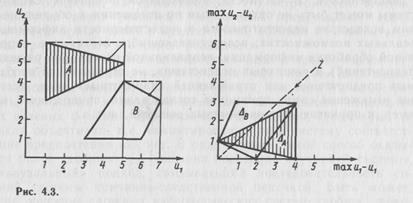 В качестве иллюстрации рассмотрим пример согласования интересов, показывающий нетривиальность проблемы возникновения единого критерия оптимальности.
В качестве иллюстрации рассмотрим пример согласования интересов, показывающий нетривиальность проблемы возникновения единого критерия оптимальности. Еп в соответствии со следующим принципом компромисса: выбираемая точка приносит каждой из подсистем одинаковый «ущерб» по сравнению с наилучшей точкой по ее критерию ui(х). Другими словами, выбираемая точка к является решением следующей задачи:
Еп в соответствии со следующим принципом компромисса: выбираемая точка приносит каждой из подсистем одинаковый «ущерб» по сравнению с наилучшей точкой по ее критерию ui(х). Другими словами, выбираемая точка к является решением следующей задачи:
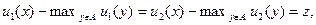
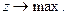 (5.40)
(5.40)