
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение интервальной целевой функции
Экспертов
Как было отмечено ранее, социально-экономическая деятельность людей включает не только такое поведение, результатом которого становятся те или иные состояния самого субъекта (спрос, миграция и т. п), но и такое, результатом которого являются состояния управляемого субъектом объекта. Это управляющее поведение субъекта, как и любые другие, определяется его отношением, предпочтением, часто заданным на множестве возможных состояний объекта, поскольку субъект в состоянии своими действиями или актами управления «выводить» объект в любое из них. Не обсуждая в данный момент, хороши или плохи предпочтения эксперта-управленца, приводящие к плановым и управленческим решениям, заметим, что эти предпочтения входят в социально-экономическую систему в качестве непременной составляющей, и поэтому их надо изучать, моделировать, а когда необходимо, и воздействовать на них. Анализу экспертных оценок, их моделированию и т. д. посвящено огромное количество экономических, психологических и математических исследований. Сложилось целое научное направление по математическому анализу мнений экспертов, принявшее в нашей стране определенные организационные формы. Так, уже много лет плодотворно и эффективно функционирует Комиссия по экспертным оценкам Совета по кибернетике РАН, которая проводит регулярно научные семинары и издала целую серию статей, трудов и монографий. В этой области предложено и проанализировано большое количество моделей экспертных предпочтений и схем, пригодных для агрегированного представления мнений разных экспертов, для определения степени из согласованности и компетентности для выработки практических решений. В данной работе мы не будем касаться всех многочисленных аспектов этого направления. Нас будут интересовать только вопросы непосредственного построения интервальной шкалы измерения предпочтений управленцев-экспертов, кроме того, мы хотим разобрать конкретный пример целевой функции для регионального планирования. Этот пример, хотя и является несколько условным, тем не менее дает вполне определенное представление о прикладных возможностях рассматриваемого подхода. Необходимость математического описания предпочтений экспертов, принимающих плановые и управленческие решения, прежде всего вызывается растущими, сложностью и объемом информации, ее динамизмом, потребностью освободить экспертов от рутинной работы с помощью ЭВМ, автоматизированных систем управления.
Наивные представления о полном вытеснении человека машиной в процессах экономического управления уступили в настоящее время место стремлению создавать человеко-машинные диалоговые системы, в которых за человеком остается творческая часть выработки решений и «последнее слово», а машина, обрабатывая большой объем информации, остается лишь его партнером и помощником. В сложных процедурах принятия плановых решений ЭВМ может помочь и в уточнении самих предпочтений человека. Как известно, человек ошибается гораздо чаще, чем машина, хотя в общем и знает, чего он хочет. Машина же, обрабатывая информацию о действиях эксперта, может смоделировать, восстановить его целевую функцию и показать далее, какие решения будет принимать человек и к чему они могут привести. Эксперт, видя последствия принимаемых им решений на основе сложившегося предпочтения, может пересматривать его, уточнять, так что человеко-машинная система становится самосовершенствующейся. Разумеется, для того чтобы машина могла восстанавливать предпочтения эксперта, человека, необходимо, чтобы сам человек заложил в нее некоторую модель своего поведения. Целевая функция, описывающая предпочтение субъекта или эксперта, характеризует уровень удовлетворения его потребностей или степень оценки им данной альтернативы. Однако можно сравнивать качество альтернатив друг с другом и с помощью некоторых «индикаторов», не обязательно отражающих всю структуру предпочтения, а полученных при некоторых дополнительных предположениях, уменьшающих общее число возможных альтернатив, наложением некоторых структурных условий. Так, например, можно сравнивать уровни удовлетворения материальных потребностей населения в разных районах по потреблению мяса, однако никто не будет считать целью материального потребления увеличение среднедушевого потребления мяса, которое может быть индикатором уровня потребления лишь при определенной структуре всего потребления. Особенно часто возникает ситуация установления соответствующего индикатора, когда необходимо оценить и сравнить уровни сложившихся состояний с точки зрения некоторых нестрого формализованных критериев «социально-экономического развития», «общего прогресса» и т. д. Именно эти случаи рассматриваются ниже в примерах на восстановление предпочтений экспертов.
Рассмотрим ситуацию, в которой плановику-эксперту приходится принимать решение, и опишем ее формальную сторону математически. Пусть состояния объекта, оптимизируемые планово-управленческими решениями, характеризуются набором переменных (вектором) х = (х1, х2,..., хп). Пусть эксперт имеет «плановое» предпочтение, описываемое интервальной целевой функцией и(х), заданной на множестве состояний х Поведением эксперта и в том, и другом случае будут ответы на вопросы специальной анкеты, хотя можно учитывать и его реальное поведение в процедурах принимавшихся решений. Основным методом для восстановления порядковой полезности служит разработанная Л. Терстоуном и развитая многими зарубежными и российскими учеными процедура парных сравнений. В ее основе лежит попарное упорядочение объектов и приписывание на базе этого каждому из них некоторого числа. Предполагается, что по значениям векторов состояния хi и хj эксперт «подсознательно измеряет» значения функции u' = и(х'), uj = u(хj) и, «сравнивая» их между собой, говорит, какой из объектов «лучше». Однако «вычисление» значений и' и uj эксперт производит с ошибкой, так что вместо истинных значений будут сравниваться значения (и' + Если указанные предположения выполняются, то при сравнении двух состояний хi и хj объект i будет признан экспертом лучше объекта j, когда (и' +
рij = Вычислив этот интеграл, можно получить рij = где Ф ( о Таким образом, вероятность того, что эксперт предпочтет объект i при сравнении его с объектом j, есть известная функция разности «истинных» значений полезности этих объектов. Функция эта — строго монотонная, изменяющаяся от нуля (когда объект j «бесконечно лучше» объекта i) до единицы (когда ситуация противоположна). Однако в этих крайних случаях формулой пользоваться не очень удобно, так как небольшим изменениям значения вероятности рij могут соответствовать слишком большие разности «истинных» полезностей (uj—ui). Так или иначе, если объекты сравнивались не одним экспертом, а несколькими (ошибки которых подчиняются одному и тому же статистическому закону распределения), то можно принять в качестве оценки вероятности рij долю экспертов, предпочитавших объект i объекту j. Имея множество объектов и соответственно пар сравнения, дающих оценки рij, можно решить систему, составленную из уравнений вида (4.15), и получить наиболее подходящие оценки значений полезностей на объектах и(х). После этого нетрудно, задавшись каким-либо определенным видом функции и(х), например квадратичной, найти ее параметры с помощью регрессионного анализа. В результате будет построена функция и (х), описывающая предпочтения экспертов. Лабораторией моделирования социальных факторов РАН были проведены экспериментальный опрос экспертов и обработка полученной информации, приведшая к представлению предпочтений экспертов с помощью квадратичной функции полезности. Объектами были условные «регионы», а состояния их характеризовались значениями показателей: х1 -месячный среднедушевой доход, х2 — обеспеченность жилой площадью на душу, х3 — годовое потребление мяса на душу, х4 — обеспеченность дошкольными учреждениями. Расчеты показали, что найденная целевая функция экспертов достаточно удовлетворительно характеризует их предпочтения. Найденную функцию и(х) можно далее уточнить, доведя ее до интервальной W(x) спомощью дополнительного опроса экспертов и применения формулы (3.25), которую запишем в виде W(x) = v [
Функция
Порядковая функция полезности, найденная методом главных компонент, оказалась следующего вида: Q(x)= 0,587 x1+ 0,459 x2+ 0,405x3+ 0,530 x4. В качестве кривой x = x(s) использовались четыре прямые, задаваемые уравнениями типа (3.14): x = xk(s) = х° + где параметр s соответствует каждый раз приросту единственной изменяемой компоненты k вектора х (рис. 3.4). Начальная точка имела компоненты: х° = (90, 9, 54, 20). По функции Q(x) и начальной точке легко находятся четыре (по числу кривых xk(s))линейные функции c = c = откуда s = ( В нашем случае они имеют вид:
Теперь, если для каждого k удастся определить vk(s) — ИФП параметра s, то можно будет построить четыре варианта ИФП, которые в идеальном случае должны совпадать: uk(s) = vk (ak Опишем процедуру опроса экспертов для нахождения функций vk(s), характеризующих уровень социально-экономического развития региона при фиксированных значениях трех (из четырех) компонент и при значении компоненты k, равном (
Предположим, что вблизи выделенных точек можно воспользоваться кусочно-линейной аппроксимацией функции v(s), как об этом говорилось выше. Тогда, опросив экспертов, задающих разные значения эквивалентных приращений, можно усреднить величины
Таблица 4.2
Эквивалентные изменения   среднемесячного душевого дохода при разных состояниях региона среднемесячного душевого дохода при разных состояниях региона
Второй столбец табл. 4.2 дает разные начальные изменения параметра s:
Так как найдены значения функции q(sl) только в точках q(sl) = e - Параметр
Интегрируя затем (3.17), получим (для каждого из четырех индексов k)
Подставляя в (3.18) вместо sk его выражения через с, получим
где через ak и bk обозначены соответствующие значения из соотношений (4.16). Таким образом найдено четыре варианта интервальной функции полезности главной компоненты с. Поскольку получившиеся функции uk(c) разные, их необходимо усреднить, преобразовав предварительно каждую положительным линейным преобразованием так, чтобы в некоторой одной и той же «средней» точке s они все имели одинаковое значение и одинаковые производные (равные все, например, единице). Найдем константы Ak и Bk линейного преобразования, приводящего функцию uk(c) к нужному масштабу. Имеем в некоторой точке с°:
Соотношения (3.19) и (3.20) дают: Ak = Окончательно получим: u(c) = u(x) = В заключение обсудим методическую сторону проблемы построения и использования ИФП типа (4.22). Прежде всего необходимо отметить исключительно важную роль экспертов и в методе парных сравнений для восстановления порядковой функции, и (особенно) при построении ИФП параметра кривой x(s). Как показывают эксперименты, опрашиваемые эксперты должны достаточно серьезно относиться к решению своей задачи по заполнению анкеты. Ответы на вопросы анкеты не должны даваться между делом, в свободную минутку, как часто бывает, им надо уделять столько времени, сколько требуется для того, чтобы серьезно продумать аргументы, в соответствии с которыми ответ будет тот, а не другой. Предположение о том, что существует интервальная шкала для измерения некоторого индекса социально-экономического развития региона, автоматически предполагает существование ИФП vk(sk) = vk(xk — xk0). Возможность экспертных оценок эквивалентных изменений переменной xk в разных точках при условии убывания функции qk (xk — xk0) означает, что эксперт считает более значимым увеличение уровня развития у менее развитых районов, чем у более развитых (при прочих равных), и может указать, в какой мере. Однако это не означает безусловной необходимости выравнивания значений индекса и независимо от значений других характеристик региона. Для того чтобы говорить о целевых функциях планирования развития регионов, надо не только иметь информацию об «обобщенном потреблении», даваемую функцией и(x1, x2, х3, х4), но и информацию об «обобщенных затратах» — вкладе региона в экономическое развитие всей страны. Сопоставление по регионам этих индикаторов друг с другом может указать «истинное» положение регионов и служить основой для формулировки регионального критерия оптимальности.
|
|||||||||||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 213; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.104.248 (0.036 с.) |
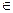 X. Предполагается, что эксперт способен из любой пары состояний х1 и х2 выбрать «лучшие», т. е. высказать, на каком из них ИФП принимает большее значение. Кроме того, предполагается, что, как было отмечено в п. 4.1, эксперт может указать и эквивалентные изменения отдельных переменных, соответствующие равным изменениям целевой функции. Первое предположение позволит по наблюдениям за «поведением» определить порядковую функцию Q(x), второе предположение даст возможность сделать ее интервальной. Мы рассмотрим оба эти этапа раздельно.
X. Предполагается, что эксперт способен из любой пары состояний х1 и х2 выбрать «лучшие», т. е. высказать, на каком из них ИФП принимает большее значение. Кроме того, предполагается, что, как было отмечено в п. 4.1, эксперт может указать и эквивалентные изменения отдельных переменных, соответствующие равным изменениям целевой функции. Первое предположение позволит по наблюдениям за «поведением» определить порядковую функцию Q(x), второе предположение даст возможность сделать ее интервальной. Мы рассмотрим оба эти этапа раздельно. 1) и (uj +
1) и (uj + 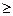 (uj +
(uj +  .
. . (4.15)
. (4.15)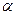 ) =
) = 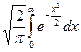 находится по соответствующим таблицам.
находится по соответствующим таблицам. (u(x)) ].
(u(x)) ].
 ,
, (s):
(s): ,
, .
.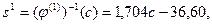

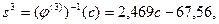
 (4.16)
(4.16) + bk).
+ bk). + sk ). В этом случае экспертам предлагается рассмотреть N состояний «типичного» региона х°, х1,..., хN-1 отличающихся только значениями компоненты k:
+ sk ). В этом случае экспертам предлагается рассмотреть N состояний «типичного» региона х°, х1,..., хN-1 отличающихся только значениями компоненты k:  ,
, 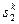 , …,
, …,  , и указать, какие должны быть изменения в значениях k -й компоненты
, и указать, какие должны быть изменения в значениях k -й компоненты  , j = 1, 2,..., N —1 каждого из состояний, чтобы компенсировать увеличение уровня социально-экономического развития за счет изменения компоненты k в состоянии х° на
, j = 1, 2,..., N —1 каждого из состояний, чтобы компенсировать увеличение уровня социально-экономического развития за счет изменения компоненты k в состоянии х° на  . To есть требуется определить набор из N эквивалентных (в смысле приращения индекса социально-экономического развития) величин параметра sk:
. To есть требуется определить набор из N эквивалентных (в смысле приращения индекса социально-экономического развития) величин параметра sk: ~…~
~…~ 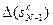 .
. =
=  /
/  по всем экспертам (i). В качестве примера приведем часть таблицы, в которую заносится информация, полученная от экспертов (табл. 3.2).
по всем экспертам (i). В качестве примера приведем часть таблицы, в которую заносится информация, полученная от экспертов (табл. 3.2).
 а следующие столбцы дают эквивалентные ему изменения дохода при другом уровне обеспечения
а следующие столбцы дают эквивалентные ему изменения дохода при другом уровне обеспечения  и затем qi усреднить по всем экспертам:
и затем qi усреднить по всем экспертам: .
. , можно сгладить эти значения методом наименьших квадратов. Полагая, что функция q(sl) — убывающая с коэффициентом
, можно сгладить эти значения методом наименьших квадратов. Полагая, что функция q(sl) — убывающая с коэффициентом  экспонента, которая в точке
экспонента, которая в точке  равна единице, имеем
равна единице, имеем .
. . (4.18)
. (4.18) , (5.19)
, (5.19) (с°) = Ak uk (с°) + Bk = 1
(с°) = Ak uk (с°) + Bk = 1  k,
k, 
 , Bk = 1 - Ak uk (с°). (4.21)
, Bk = 1 - Ak uk (с°). (4.21) ,
, (0,587x1 + 0,459 x2 + 0,405 x3 + 0,530x4). (4.22)
(0,587x1 + 0,459 x2 + 0,405 x3 + 0,530x4). (4.22)


