
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формальный аппарат теории интервальной
Полезности
Прежде чем получить выражение F(t)в явном виде, необходимо доказать ряд промежуточных утверждений. Лемма 1. Пусть v(t) — непрерывно дифференцируемая и строго возрастающая функция, заданная на отрезке [t0, t1] c производной v'0 в точке t0. Пусть также t — точка отрезка [t0, t1],
v(t0 +
Тогда имеет место следующее равенство: v(t) = v(t0 ) + v'0 Доказательство. Так как для функции v(t) всегда выполняется равенство v(t) = v(t0 ) + Рассмотрим условие (2.13), которому должны удовлетворять приращения аргумента
При этом Перепишем теперь (2.13) в виде
где через
Так как при q(t) = что и требовалось доказать. В дальнейшем нам будет необходимо воспользоваться ещё одним математическим результатом. Лемма 2. Пусть непрерывные функции f(x) и F(x) определены на односвязном компакте x (I) f(x) = kF(x) + l, x (II) {f(x1) - f(x2) = f(x3) - f(x4)} (III) x1, x2, x3, x4 Доказательство. Справедливость условия (II) при выполнении условия (I) проверяется простой подстановкой. Докажем справедливость условия (I) при выполнении условия (II). Образуем два множества Z и W следующим образом: Z = {z: z = F(x), x Так как X — односвязный компакт, а функции F(х) и f(x) непрерывны, то, очевидно, множества Z и W суть отрезки. Построим отображение точек множества W на множество Z следующим образом: L(w) = {z: z = F(x), w: w = f(x), x Так как для каждого w Нашей целью будет показать, что: 1) отображение L(w) есть однозначная функция своего аргумента: z = L(w); 2) L(w) удовлетворяет условию
для любых w1,w2 Î W; 3) L(w) — непрерывна.
Далее можно будет воспользоваться тем фактом, что если некоторая непрерывная функция
то она линейна, т. е. существуют константы а
Докажем однозначность отображения (3.18) от противного. Пусть существуют z1 f(x1) - f(x3)= f(x2) - f(x3), в то время как F(x1,)—F(x3) w3 = Для w1 имеет место равенство w1 — w3 = w3— w2, wi По определению множества W существуют xi f(x1) - f(x3)= f(x3) - f(x2). По условию леммы 2 аналогичное равенство выполняется и для функции F(x): F(x1)—F(x3) =F(x3)—F(x2) или F(x3)=
Докажем теперь непрерывность функции z = L(w), w F(xnk) Но это означает, что L Непрерывность доказана, а тем самым доказана вся лемма. Обратимся к нахождению функции F(t) для перехода от порядковой полезности к интервальной. Пусть нам дана кривая x = x(s), пересекающая поверхность безразличия (параметр s изменяется от s0 до s1, и каждому s соответствует свое значение х). Пусть кривая x(s) при этом пересекает каждую из поверхностей безразличия ровно в одной точке, т.е. решение уравнения Q(x(s))=c относительно s единственно. Обозначим через
Очевидно, в силу сказанного при s0
c = Поскольку каждое значение параметра s определяет некоторый уровень порядковой полезности, функцию v(s) =u(x(s)), s Функции v(s), определенные соотношением (3.21), действительно интервальны, так как между произвольными функциями v(s) и V(s), индуцируемыми функциями и(х) и U(x), должна выполняться связь v(s) =u(x(s)) = Если обозначить значения функции и(х) через D, получим v(s) = D, s = поскольку между s и D тоже существует взаимно однозначное соответствие. По этой причине по любому значению одного из трех параметров с, D, s можно найти значения остальных двух. В частности, D = v[ причем эти формулы устанавливают связь между константами одних и тех же поверхностей безразличия Q(x)=c, и(х) = D, когда Q(x) и и(х) отличаются друг от друга произвольным строго монотонным преобразованием. Нам понадобится еще небольшая лемма. Лемма 3. Функция s(x) = Доказательство. Наряду с функцией s(x) =
Содержательно функция s(x) выражает значение параметра s, при котором кривая x(s) пересекает ту поверхность безразличия, уравнение которой может быть представлено в виде Q(x)=Q( Основная идея перехода от порядковой полезности к интервальной заключается в том, чтобы приписать каждой поверхности безразличия (которые одинаковы у Q(x) и и(х)) не с-значения уровня порядковой полезности, а D-значения интервальной полезности, отвечающие соответствующим значениям параметра s. Другими словами, если известны функции Q(x), c = u(x) = v( Этот результат сформулируем в виде теоремы. Теорема 1. Пусть на выпуклом компакте Х Доказательство. Сначала заметим, что Ф(х), имея одни и те же поверхности безразличия с Q(x), связана с нею положительным монотонным преобразованием, поскольку функции v(s) и Покажем теперь, что Ф(х) имеет равные приращения в тех точках и только в тех, в которых некоторая интервальная функция полезности и(х) имеет равные приращения. Тогда по лемме 2 можно будет сделать вывод о том, что Ф(х) и и(х) связаны положительным линейным преобразованием, а значит, принадлежат одному классу интервальных функций полезности.
Пусть в точках х1, х2, х3, x4 U(х1) - U(х2) = U(х3) - U(х4). (3.26) Так как каждую из поверхностей, определяемых уравнениями U(х) = U(хi ), i=1, 2, 3, 4, кривая x(s) пересекает при единственном значении параметра s = si, то можно записать U(x(s1))-U(x(s2))=U(x(s3))-U(x(s4)) (3.27) или V(s1)-V(s2)=V(s3)-V(s4), (3.28) где V(s) = U(x(s)) -- «интервальная функция полезности» параметра s, индуцируемая функцией U(x). Поскольку заданная условиями теоремы функция v(s) есть некоторая интервальная функция полезности параметра s, то для нее тоже должны выполняться аналогичные равенства: v(s1) — v(s2)= v(s3) — v(s4). (3.29) В силу того, что si суть значения параметра, соответствующего поверхностям безразличия и(х) = u(хi), а значит, и Q(x) = Q(хi), можно записать, что si = s(хi) = v[ или Ф(х1)-Ф(х2)=Ф(х3)-Ф(х4). (3.31) Докажем теперь справедливость обратного утверждения. Пусть в точках xi Так как V[ где и(х) — интервальная функция полезности, которой соответствует функция v(s) = u(x(s)). В результате получаем u(xl) - u(x2) = и(х3) - и(х4). Последнее равенство завершает доказательство теоремы.
|
|||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 227; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.199.162 (0.04 с.) |
 (t)>0 и
(t)>0 и  dt при
dt при 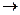 0 и
0 и  t
t 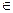 [t0, t1]. (2.14)
[t0, t1]. (2.14) (s)ds, то остаётся показать, что
(s)ds, то остаётся показать, что  при
при 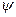 [
[  [
[  означает функцию, обратную к
означает функцию, обратную к  .
. (3.15)
(3.15) обозначена величина бесконечно малого порядка по сравнению с
обозначена величина бесконечно малого порядка по сравнению с  при
при 
 имеет предел, равный
имеет предел, равный ;
; {F(x1) - F(x2) = F(x3) - F(x4)};
{F(x1) - F(x2) = F(x3) - F(x4)};
 (х) на отрезке из E1, удовлетворяет условию
(х) на отрезке из E1, удовлетворяет условию
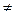 0 и b, такие, что
0 и b, такие, что
 , что означает z3 =
, что означает z3 =  или
или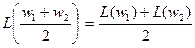
 и покажем, что последовательность точек zn = L(wn) сходится к
и покажем, что последовательность точек zn = L(wn) сходится к  . Очевидно, существуют точки xn
. Очевидно, существуют точки xn  можно выделить сходящуюся подпоследовательность
можно выделить сходящуюся подпоследовательность  , так что xnk
, так что xnk  . В силу непрерывности функций f(x) и F(x) на точках выделенной подпоследовательности имеет место
. В силу непрерывности функций f(x) и F(x) на точках выделенной подпоследовательности имеет место , f(xnk)
, f(xnk) 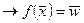 .
. , поскольку
, поскольку ={
={  :
:  ),
),  =f(
=f(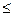 s
s  (c). (3.20)
(c). (3.20)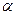 U(x(s)) +
U(x(s)) +  =
=  (D), (3.23)
(D), (3.23)
 (x) =
(x) = 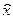 ) =
) =  ) =
) =  ))] =
))] =  Еn определены непрерывные функции и(х) и Q(x), причем функция и(х) есть неизвестная интервальная функция полезности, а Q(x) задает ее поверхности безразличия Q(x)=c. Пусть, далее, однопараметрическая кривая x = x(s), у которой нет самопересечений, пересекает каждую из поверхностей безразличия ровно в одной точке, так что между значениями параметра s и функций Q(x), u(x) устанавливаются взаимно однозначные соответствия c =
Еn определены непрерывные функции и(х) и Q(x), причем функция и(х) есть неизвестная интервальная функция полезности, а Q(x) задает ее поверхности безразличия Q(x)=c. Пусть, далее, однопараметрическая кривая x = x(s), у которой нет самопересечений, пересекает каждую из поверхностей безразличия ровно в одной точке, так что между значениями параметра s и функций Q(x), u(x) устанавливаются взаимно однозначные соответствия c = 


