
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Целевые функции экономического поведения
Моделирование потребительского спроса с Помощью целевых функций
Наиболее известна и широко используется в самых различных экономико-математических моделях и прикладных исследованиях следующая модель поведения рыночного потребителя: Q(x) (p, x) «Потребителем» здесь является семья определенного типа, х — n-мерный вектор продукции, потребляемой в течение фиксированного промежутка времени, р — вектор соответствующих цен, s — доход, Q(х) — порядковая функция полезности. Данная модель представляет собой конкретизацию модели выбора из гл. 2 при явном задании допустимого множества альтернатив (вариантов семейного потребления) с помощью цен р и дохода s. Простота делает модель особенно удобной при планировании уровня жизни и расчетах возможного потребления (спроса) семей, когда экономические условия, в которых они находятся, — цены и доход — меняются известным образом. Однако определение функции Q(х), описывающей структуру потребительского предпочтения семьи, задача не совсем простая. Кроме того, до сих пор встречается негативное отношение к использованию подобных функций полезности в плановых расчетах, аргументированное тем, что ориентироваться на сложившееся потребительское предпочтение неправильно, потому что с точки зрения общественных интересов потребление населения должно быть не таким, как оно того хочет, а таким, каким ему надлежит быть. По этому поводу можно заметить, что использование в экономических расчетах для планирования или прогнозирования функций полезности вовсе не означает ориентации планирования на сложившуюся структуру предпочтения, которая в ряде случаев действительно может приводить к нежелательным с точки зрения общества явлениям. Но что бы ни предпринимали плановые или какие-либо другие органы, население, группы, индивид всегда ведут себя так, как это соответствует их собственным предпочтениям и как это допустимо с точки зрения внешних условий, определяющих множество возможных альтернатив X. Поэтому не принимать во внимание имеющееся предпочтение социально-демографических групп, значит закрывать глаза на реальность и принимать заведомо неправильные плановые решения. Если же необходимо изменить сложившуюся структуру потребления каких-либо групп населения, то для этого есть только два метода: изменить условия, в которых находится группа (в нашем случае менять цены р и доход s), или изменять само предпочтение, функцию Q(x) с помощью соответствующих воспитательных мер, рекламы, разъяснения и т. п.
Предложено большое число различных методов, позволяющих на базе статистики бюджетных обследований находить параметры функции Q(х). В основном все методы предназначены для построения уравнений поверхностей безразличия, хотя имеются и такие, которые при некоторых дополнительных предположениях дают возможность определять эту функцию более точно — с точностью до линейного преобразования. Обозначим оптимальное решение задачи (4.1), т. е. рациональное поведение потребителя, через х°. Пусть вектор цен не меняется, а доход данного потребителя принимает какие-то значения между s0 и s1: s0 В этом случае поведение х° будет функцией от s: х° = х°(s), называемой функцией спроса. Зная вид этой функции, можно построить порядковую функцию полезности дохода
Выражение (4.3) подчеркивает, что деньги, доход сами по себе ценности для потребителя не имеют, их «полезность» определяется лишь в той степени, в какой они могут быть превращены в потребляемые продукты, вектор х°. Разумеется, такое представление о значимости денег для потребителя не всегда может быть достаточно справедливым. В ряде моделей предполагается, что и сама функция полезности и(х) зависит от дохода по крайней мере как от параметра: и(х) = иs(х). Такое предположение, по-видимому, имеет смысл использовать только в том случае, когда допустимое множество альтернатив не является множеством вида {х: х Если функция Q(х) строго выпуклая, то решение задачи (3.1) единственно (поведение потребителя определяется однозначно) и кривая х = х°(s) пересекает поверхности безразличия Q(x) = const только в одной точке.
С ростом величины s множество допустимых наборов потребления «увеличивается»: {х: х По этой причине и в силу положительности частных производных Ситуация оказывается аналогичной разобранной в п. 3: между значениями дохода s и величинами с, определяющими поверхности безразличия, имеется взаимно однозначное соответствие: c = Кривая х = х°(s) (рис. 4.1), как кривая в пространстве Еп потребительских благ, называется кривой Энгеля. Изучению этих кривых посвящено много работ, в частности, они используются в моделировании экономики на государственном уровне для выявления глобальных целевых функций. Как перейти от порядкового измерения полезности к количественному? Может показаться, что поскольку каждому значению с функции порядковой полезности (Q(x) =с) соответствует ровно одно значение дохода s, а доход измеряется в числах, то, взяв в качестве меры полезности рубли, мы получим сразу количественное выражение полезности в рублях: s(x) = Выражение (4.4) можно назвать «компенсированным доходом», потому что содержательно величина s(х) равна тому количеству дохода s, которое может гарантировать потребителю достижение уровня удовлетворения потребностей (уровня полезности), не меньшего, чем набор х: Q(х). Можно показать, что
x- Однако нет никакой гарантии, что всякий раз, когда имеет место отношение предпочтения (4.6), будет выполняться
В частности, пусть s(x) = 3000 руб., s(у) = 1000 руб., s(х') = 3150 руб., а s(y') = 1100 руб. Тогда
Поскольку предполагается, что рассматривается один и тот же потребитель (функция полезности одна и та же при разных уровнях дохода) в разных состояниях в смысле его дохода, то, несмотря на превышение прироста большего его дохода (150 руб.) над приростом меньшего дохода (100 руб.), более предпочтительными могут оказаться именно 100 руб., а не 150. В результате между требованиями (4.6) и (4.7) возникает явное противоречие. Кроме того, известен такой экономический факт, что прирост дохода на 1 руб. тем меньше значим для потребителя, чем больше сам доход. Этот факт описывается на экономико-математическом языке как падение предельной полезности дохода при его росте. Под предельной полезностью дохода понимают объективно обусловленную оценку (множитель Лагранжа) бюджетного ограничения задачи (4.1). Как и прямое решение задачи (4.1) х°, двойственное решение
При некоторых естественных предположениях двойственная оценка совпадает с производной оптимального значения целевой функции задачи (4.1) по правой части ограничения s, поэтому
Как было отмечено, величина
Ввиду важности этого факта как в прикладном, эмпирическом плане, так и в чисто теоретическом (он будет использован в формально-математических доказательствах п.6), придадим ему вид самостоятельной леммы.
Пусть целевая функция Q(х) модели (4.1) имеет строго положительные частные производные, строго выпукла, вектор р > 0, а оптимальное решение х° — тоже строго положительный вектор. Тогда двойственная оценка s1 < s2 Доказательство. Заметим прежде всего, что в силу строгой выпуклости функции Q(х) и строгой положительности вектора х° по теореме Куна — Таккера должно выполняться равенство
Так как x°(s) – однозначная функция, значения которой меняются при изменении s, а Пусть s1 < s2 , тогда Q(x°(s1 )) - Q(x°(s2 )) < 0. В силу строгой выпуклости функции Q(x) должно выполняться следующее соотношение:
которое с учетом (4.11) дает
Рассматривая разность Q(x°(s1 )) - Q(x°(s2 )), аналогичным образом получаем
Сравнение последних двух неравенств дает
Лемма доказана. Таким образом, из факта падения предельной полезности дохода с его ростом следует, что возрастающие, но выпуклые вниз функции
Прежде чем рассмотреть иллюстрированный пример на эмпирическое определение интервальной полезности, выскажем несколько отдельных замечаний по поводу скептического отношения к самой идее существования и возможной операционализации концепции «измеримой полезности». В фундаментальной монографии П.Фишберна по теории полезности, в которой при основательном освещении математических вопросов прикладные аспекты затрагиваются лишь вскользь, признаются недостаточными попытки операционального определения «измеримых предпочтений» (хотя, по-видимому, сам автор готов в целом принять гипотезу их непосредственного существования). Указывается три способа операционализации с целью сравнения переходов х Первое замечание, которое необходимо сделать, касается общего характера рассуждений по поводу операционализации, в результате которых будто бы можно доказать или опровергнуть возможности выявления «измеримых предпочтений». По нашему мнению, говоря об операционализации, необходимо более конкретно указывать и альтернативы, и ЛПР, и ситуацию, в которой находится последнее, потому что в одних случаях данный способ может быть приемлем, а в других — совсем нет. В частности, мы рассматриваем ИФП по отношению к рыночному потребителю с целью прогнозирования спроса, по отношению к экспертам, оценивающим индекс социально-экономического развития региона (см. 4.2), и по отношению к экономике в целом. Во-вторых, нельзя ни в коей мере забывать, что речь идет не об «абсолютной истине», а только о модели, о приближенной схеме, отражающей некоторые важные свойства поведения людей и облегчающей его прогнозирование. «...Можно ли выбрать одно и только одно значение х, для которого (х долл.
В то же время имеющиеся факты могут указывать на проявление «измеримых предпочтений» в некоторых типах поведения. Как уже упоминалось, известен факт падения предельных полезностей дохода (или значимости рубля для потребителя) с ростом дохода. Но каков содержательный смысл, например, такого соотношения:
Это соотношение утверждает, что при сравнении единичных приростов доходов в 1800 и 1200 руб. первый прирост оказывается менее значим, чем второй. В рамках приводившейся выше модели поведения потребителя это означает, что соответствующие изменения в потребительских наборах тоже могут сравниваться. Если рассматривать ИФП как модель отношения индивида к его возможным состояниям, то все три способа операционализации, приведенные выше, могут быть приемлемыми в зависимости от конкретной ситуации. Конечно, если оценка лотерей осуществляется с позиции «субъективных вероятностей», введение которых, на наш взгляд, имеет смысл только при моделировании индивидуального поведения, то здесь может быть что угодно. Однако если вероятность трактуется статистически как некоторая устойчивая характеристика массовых явлений, то индивиду будет заведомо выгоднее ориентироваться на среднее. Операционализация через сравнение замещений, по-видимому, уже не должна никого смущать. В прекрасно написанной книге Р. Л. Клини и X. Райфа, посвященной целиком прикладным аспектам теории полезности, эта идея многократно и эффективно используется на конкретном материале. В частности, и третий способ операционализации оказывается просто способом, позволяющим проводить соответствующие сравнения, например в процедурах экспертных оценок. Разумеется, в каждом конкретном случае сам вид соответствующего опроса должен быть тщательно разработан применительно к изучаемой ситуации. Рассмотрим условный пример эмпирического определения функции v(s). Основой для построения функции могут служить эквивалентные приращения доходов в начальной точке s0 и в остальных точках s. Если бы каждый потребитель из некоторой группы потребителей был в состоянии указать по отношению к некоторой последовательности { Эквивалентные приращения необходимы для получения функции v(s). На основании общих соображений, а также некоторого опыта опроса потребителей можно выделить два более простых случая. Первый случай заключается втом, что эквивалентные приращения оказываются пропорциональными самим величинам доходов, т. е.
Очевидно, в этом случае v (s) = a+b
В этом случае нет трудностей статистического определения предела и достаточно для каждого s взять среднее из отношений Отметим, что определяемая решением экстремальной задачи (4.1) предельная полезность дохода
Рассмотрим небольшой условный пример на вычисление функции v(s). Предположим, опрошено 10 «экспертов» — представителей групп семей, состоящих из 4 человек, из которых двое не работают, третий имеет среднемесячный заработок 10000 руб., а четвертый попеременно 8500, 13500, 17500, 25000, 35000 руб. В соответствии с этим среднедушевые доходы принимают значения: s0 = 4625 руб., s1 = 5875 руб., s2 = 6875 руб., s3 = 8750 руб.; s4= 11250 руб. «Экспертам» предлагалось определить эквивалентные изменения в зарплате одного из членов семьи при двух уровнях этой зарплаты: 8500 и 13500 руб., 8500 и 17500; 8500 и 25000; наконец, 8500 и 35000руб. Конкретно, они должны были ответить на вопрос: на сколько надо увеличить зарплату в 13500 руб., чтобы ее прирост был так же значим для семьи, как прирост зарплаты от 8500 до 9000 руб.? Затем такой же вопрос ставился по отношению к уровням зарплаты в 17500, 25000 и 35000 руб. После этого опрос «экспертов» повторялся, но вместо уровня зарплаты в 90000 руб. он относился к уровню в 9500 руб. (10500 руб. и т. д.). Усредненные мнения «экспертов» относительно эквивалентных приращений Величины q(si), i= 1, 2, 3, 4, вычисляем по формуле
Для табл. 3.1 q(si) равны соответственно: q(s1) =0,56, q(s2) =0,37, q(s3) =0,30, q(s4) =0,23. Таблица 4.1.
Вместе с очевидным значением q(s0) = 1 мы имеем пять точек кривой q(s) (рис. 4.3). Методом наименьших квадратов можно найти параметры кривой второго порядка q(s) = a0 + a1s + a2s2, приближающей искомую функцию и проходящей через точку s0 = 46,25, q(s0) = 1. Для этого необходимо решить следующую задачу на условный экстремум:
a0 + a1s0 + a2 Решив эту задачу, можно найти, что a0 = 37,83, a1 = — 1,152, a2 = 0,008. Уравнение искомой кривой имеет вид q(s) = 37,83—1,152 s + 0,008 s2. Теперь можно определить интервальную функцию полезности дохода: v(s) = Так как выбор констант
Тогда функция v(s) представится в виде v(s) = s - Заметим, что не только доход может служить в качестве параметра кривой x(s), так что для него находятся эквивалентные приращения x = y(s) = В этом случае изменяется значение только одной переменной, а остальные значения фиксированы.
Функция v(s) тогда оказывается функцией полезности одного блага (уровни других благ заданы). В ряде случаев использование в качестве параметра самих некоторых переменных оказывается более удобным, так как экспертам проще говорить об эквивалентных изменениях переменных, а не об изменениях абстрактных параметров кривой.
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 262; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.47.14 (0.055 с.) |
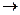 max,
max,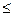 s, x
s, x 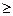 0. (4.1)
0. (4.1) (s) = Q(х° (s)). (4.3)
(s) = Q(х° (s)). (4.3) {х: х
{х: х  оптимальное значение Q(x°) тоже строго увеличивается (на «большем» множестве максимальное значение функции больше, чем на «меньшем» множестве, содержащемся в «большем»). Но это означает, что
оптимальное значение Q(x°) тоже строго увеличивается (на «большем» множестве максимальное значение функции больше, чем на «меньшем» множестве, содержащемся в «большем»). Но это означает, что  (c).
(c). s(x) =
s(x) = 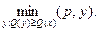 (4.5)
(4.5) (4.6)
(4.6)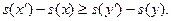 (4.7)
(4.7)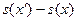 = 150 руб. > 100 руб. = s(y') – s(y).
= 150 руб. > 100 руб. = s(y') – s(y). ° будет функцией дохода:
° будет функцией дохода: . (4.9)
. (4.9) и эмпирически установлено, что
и эмпирически установлено, что  убывает с ростом s (рис. 4.2).
убывает с ростом s (рис. 4.2).
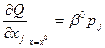 . (4.11)
. (4.11)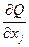 - однозначная функция x°, а значит, и s, то из приведенного равенства (4.11) следует, что
- однозначная функция x°, а значит, и s, то из приведенного равенства (4.11) следует, что  x°(s1 )) > Q(x°(s2 )) - Q(x°(s1 )) > 0,
x°(s1 )) > Q(x°(s2 )) - Q(x°(s1 )) > 0, не могут быть приняты в качестве интервальной функции полезности дохода, так как для них функция
не могут быть приняты в качестве интервальной функции полезности дохода, так как для них функция 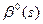 будет возрастающей. Возникает естественный вопрос: а нельзя ли, основываясь на эмпирическом факте существования предпочтения на локальных приращениях дохода, явно выразить это предпочтение с помощью интервальной функции полезности дохода v(s)? Так как ситуация оказывается совершенно аналогичной рассмотренному ранее общему случаю восстановления ИФП, то ответ на данный вопрос положителен. Кривая Энгеля x0 = x0(s) позволяет получить функцию
будет возрастающей. Возникает естественный вопрос: а нельзя ли, основываясь на эмпирическом факте существования предпочтения на локальных приращениях дохода, явно выразить это предпочтение с помощью интервальной функции полезности дохода v(s)? Так как ситуация оказывается совершенно аналогичной рассмотренному ранее общему случаю восстановления ИФП, то ответ на данный вопрос положителен. Кривая Энгеля x0 = x0(s) позволяет получить функцию  . Остается определить v(s) по формуле (2.33), предварительно найдя пределы эквивалентных приращений q(s)=
. Остается определить v(s) по формуле (2.33), предварительно найдя пределы эквивалентных приращений q(s)= 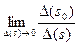 , где
, где  и
и 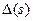 - эквивалентные приращения дохода при его уровнях
- эквивалентные приращения дохода при его уровнях  и s. Определив их непосредственным опросом потребителя (или каким-либо другим способом), можно найти q(s), затем и v(s), после чего функция полезности u(x) восстанавливается по формуле
и s. Определив их непосредственным опросом потребителя (или каким-либо другим способом), можно найти q(s), затем и v(s), после чего функция полезности u(x) восстанавливается по формуле  .
.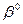 (1800 руб.) <
(1800 руб.) <  (sk) } приращений дохода в точке s0 последовательность почленно эквивалентных приращений в произвольной точке s>s0, то можно было бы пытаться после статистической обработки непосредственно пользоваться формулами (3.33) и (3.25). Однако проводить опрос потребителей с целью получения информации об эквивалентных приращениях доходов весьма сложно, так как потребитель не всегда в состоянии дать правильный ответ. Все же возможен отбор некоторого количества «экспертов» из каждой группы потребителей, которые будут в состоянии дать необходимую информацию. Наконец, как уже отмечалось, можно представить саму проблему несколько в иной плоскости, считая, что речь идет об установлении «эквивалентных по справедливости» изменений доходов у групп, отличающихся по размерам дохода. В этом случае функция v(s) должна так упорядочивать группы потребителей, чтобы ее изменения в одной области могли указывать необходимые компенсирующие изменения доходов в другой.
(sk) } приращений дохода в точке s0 последовательность почленно эквивалентных приращений в произвольной точке s>s0, то можно было бы пытаться после статистической обработки непосредственно пользоваться формулами (3.33) и (3.25). Однако проводить опрос потребителей с целью получения информации об эквивалентных приращениях доходов весьма сложно, так как потребитель не всегда в состоянии дать правильный ответ. Все же возможен отбор некоторого количества «экспертов» из каждой группы потребителей, которые будут в состоянии дать необходимую информацию. Наконец, как уже отмечалось, можно представить саму проблему несколько в иной плоскости, считая, что речь идет об установлении «эквивалентных по справедливости» изменений доходов у групп, отличающихся по размерам дохода. В этом случае функция v(s) должна так упорядочивать группы потребителей, чтобы ее изменения в одной области могли указывать необходимые компенсирующие изменения доходов в другой.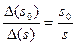 . (4.12)
. (4.12)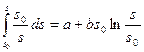 и, вообще говоря, мы получаем логарифмическую шкалу полезности доходов. Во втором случае равенство (4.12) не выполняется, но предел отношений эквивалентных приращений совпадает с самими отношениями:
и, вообще говоря, мы получаем логарифмическую шкалу полезности доходов. Во втором случае равенство (4.12) не выполняется, но предел отношений эквивалентных приращений совпадает с самими отношениями: .
.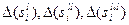 представлены в табл. 3.1.
представлены в табл. 3.1. .
. ,
,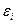 = q(si) - a0 - a1si - a2
= q(si) - a0 - a1si - a2 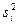 ,
,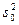 = 1, i =4, 2, 3, 4.
= 1, i =4, 2, 3, 4.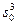 )].
)].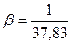 ,
, 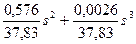 .
. . (4.14)
. (4.14)



