
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Согласование интересов при наличии «памяти»
Участников
Вернемся к общей проблеме согласования. По-прежнему i будет индексом участников коллектива I = {1, 2,..., п}, индикатором ui = Примем три следующих предположения. I. «Память» каждого участника описывается оператором самосогласования Fi (ua )x = где все ха,0, как и все ха,1, эквивалентны в смысле R1 и R2 (выполняется условие полной сравнимости). II. Коллективная функция полезности
Требуется охарактеризовать свойства оператора согласования интересов п участников F Более строго, необходимо, зная операторы памяти Fi и вид функции иа(х) для некоторого фиксированного набора Сформулируем некий принцип, который позволит решить поставленную задачу. Пусть участники коллектива при данном наборе ИФП участников согласовали свои интересы определенным образом — так, как считается «справедливым». Очевидно, изменение предпочтений у одного или нескольких участников, хотя и может привести к другой форме коллективного предпочтения, все же должно оставаться по-прежнему «справедливым», т.е. само изменение, например, весовых коэффициентов отдельных целевых функций именно тем и вызывается, что их неизменность означала бы нарушение признанной «справедливости». Необходимость сохранения установленной «справедливости» при согласовании интересов и порождает принцип, который представляется удобным назвать принципом инвариантности компромисса, поскольку каждое согласование интересов должно быть неким компромиссом. III. Итак, принимается следующий принцип инвариантности компромисса. Пусть [х, [xl тогда выполнение неравенств
влечет также выполнение неравенств
и наоборот. Другими словами, характер коллективного предпочтения не должен меняться при изменении частных предпочтений, если рассматривать вместо прежних состояний или переходов новые, эквивалентные прежним для всех участников в смысле их «памяти». Интуитивно понятно, что, зафиксировав некоторое «коллективное мнение» для некоторого набора предпочтений участников, можно будет для любого другого набора в определенном смысле перенести прежнее предпочтение на эквивалентные состояния и переходы и тем самым однозначно получить новое «коллективное мнение». Это возможно сделать, если известны правила перехода от поверхностей безразличия функций
Теорема 2. Всякий оператор согласования интересов F[ut, u2,..., un], удовлетворяющий условиям (I), (II), (III) и условиям теоремы 2, является некоторой сложной функцией от операторов самосогласования участников: F[ut, u2,..., un]x = причем Fi [ Доказательство. При каждом фиксированном наборе функций ui(х) ИФП коллектива и(х) есть сложная функция fa от ui(х); рассмотрим эту функцию для набора
где ui принадлежит отрезку La = Если существует оператор согласования, значит определены все функции fa (ut, u2,..., un), каждая в некоторых точках своего параллелепипеда La. Пусть для набора
где А и В — константы, задаваемые формулами (4.19); индексы у констант мы опускаем ради упрощения записи. Тогда условие инвариантности (4.31) — (4.32) для наших функций можно переписать в следующем виде: fa ( fa [
Здесь х, у, х1, х2, х3, x4
L + K fB [A1 Подставив вместо констант Ai, Вi их выражения, получим Ai + = = Так как при фиксировании индикатора fa ( Теорема доказана. Отсюда следует, что, вообще говоря, согласование может определяться любой непрерывной функцией п переменных, надо только определить согласование какого-то начального набора функций Важнейшим условием, позволяющим получить необходимый результат, было предложение о том, что все пары функций
В заключение приведем некоторые соображения по поводу практического определения «памяти» или «самосогласования» на базе специальной статистической информации. Еще раз подчеркнем, что развиваемая в данной работе концепция имеет целью разработку аппарата не для всех ситуаций согласования интересов, а только применительно к случаю экономико-математического моделирования в планировании, когда согласовываются не интересы участников абстрактного «коллектива» или «общества», а целевые функции определенных социально-демографических групп населения в задачах оптимального планирования. В частности, если в момент времени t принимается согласование целевых функций в виде функционала Tt ( Таким образом, при планировании на перспективу (до учета фактора дисконтирования в чистом виде) необходимо: 1) прогнозировать изменения, которые произойдут в целевых функциях социально-демографических групп; 2) произвести сравнение новых предпочтений со старыми. Первая задача сводится к прогнозированию параметров целевых функций Как было показано, наличие «памяти» или «самосогласования» в условиях интервальной шкалы полезности означает существование линейного преобразования, переводящего значения целевых функций
Таким образом, для каждой группы необходимо экспериментально определить две константы: A и B. Процедуру определения этих констант можно представить себе в следующем виде. Путем специального опроса сначала определяются наборы состояний [ здесь k — номер соответствующего наблюдения, устанавливающего пару эквивалентных значений функций
Очевидно, должны выполняться соотношения:
Последние соотношения означают, что константы А и В могут быть определены как коэффициенты соответствующей линии регрессии, определяемой совокупностью точек (пар значений)
|
|||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 198; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.187.103 (0.029 с.) |
 , будем отмечать непрерывную ИФП участника i,
, будем отмечать непрерывную ИФП участника i,  , i
, i 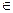 I, заданную на компакте X
I, заданную на компакте X (x), x
(x), x  (x) =
(x) =  ,
, (x) относится к классу ИФП и для каждого набора
(x) относится к классу ИФП и для каждого набора  является сложной функцией, зависящей от х только через значения функций ui:
является сложной функцией, зависящей от х только через значения функций ui:
 =
= 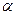

 ,
,  - два разных набора ИФП участников; в то же время пусть для любого i пары состояний х и
- два разных набора ИФП участников; в то же время пусть для любого i пары состояний х и 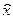 , у и
, у и 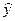 , а также пары переходов xl
, а также пары переходов xl 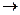 x2 и yl
x2 и yl  ] ~ [
] ~ [  ], [y,
], [y,  i,
i, (x)
(x) 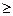
 (
( (y).
(y).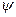 [F1 (ut ) x , F2 (u2 ) x , …, Fn (un ) x ],
[F1 (ut ) x , F2 (u2 ) x , …, Fn (un ) x ], ,
,  .
. = fa [
= fa [ 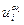 (x),
(x), 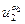 (x), …,
(x), …,  (x)],
(x)],  = { ui: min
= { ui: min 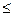 ui
ui 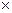

 .
.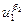 ,
,  ,...,
,...,  ), а переходы от функции
), а переходы от функции  определяются оператором самосогласования, так что
определяются оператором самосогласования, так что fB [A1
fB [A1 
 ) -
) -  )
)  (x)[
(x)[ 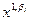 ) -
) -  (x), …,
(x), …,  (x))
(x)) 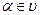 .
.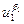 ,
,  , то значения последних —
, то значения последних —  (x) - действительно могут называться «инвариантными полезностями».
(x) - действительно могут называться «инвариантными полезностями». (y0);
(y0); 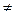
 ,...,
,...,  ), то надо уметь определить и функционал согласования Tt+1 (
), то надо уметь определить и функционал согласования Tt+1 ( ,...,
,...,  ). Изменение «вкусов» и предпочтений (функций
). Изменение «вкусов» и предпочтений (функций  ) с течением времени неизбежно приводит к необходимости сопоставления прежних предпочтений с новыми при учете в планировании на перспективу «поведения» выделенных групп.
) с течением времени неизбежно приводит к необходимости сопоставления прежних предпочтений с новыми при учете в планировании на перспективу «поведения» выделенных групп. . Вторая задача требует для каждой группы указать, какие значения ее целевой функции
. Вторая задача требует для каждой группы указать, какие значения ее целевой функции  ,
,  ,...,
,..., 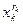 и
и  ,
,  ,...,
,...,  , k = l, 2,..., К, которые группа считает эквивалентными (в смысле «самосогласования»), т. е.
, k = l, 2,..., К, которые группа считает эквивалентными (в смысле «самосогласования»), т. е. , ut ] ~ [
, ut ] ~ [  , ut+1 ], l =1, 2,..., sk, m=1, 2,..., rk,
, ut+1 ], l =1, 2,..., sk, m=1, 2,..., rk, , k = 1, 2, …, K.
, k = 1, 2, …, K. k = 1, 2,..., К.
k = 1, 2,..., К. . К сожалению, мы не располагаем экспериментальными данными, с помощью которых можно было бы оценить эти константы.
. К сожалению, мы не располагаем экспериментальными данными, с помощью которых можно было бы оценить эти константы.


